数学杂记（技）
组合数——斐波那契等式
\(\sum\limits_{i=0}^n \dbinom{n-i}{i}=f_{n+1}\)，其中 \(f\) 为斐波那契数列。
证法 \(1\)：
\(\sum\limits_{i=0}^n \dbinom{n-i}{i}=\sum\limits_{i=0}^n [x^i](1+x)^{n-i}=[x^n]\sum\limits_{i=0}^n x^{n-i}(1+x)^{n-i}=[x^n] \dfrac{1}{1-x-x^2}=[x^{n+1}] \dfrac{x}{1-x-x^2}=f_{n+1}\)
由斐波那契数列递推式易证其生成函数式 \(\dfrac{x}{1-x-x^2}\)。
证法 \(2\)：
考虑组合意义：\(f_{n+1}\) 表示选若干个 \(1\) 和 \(2\) 和为 \(n\) 的方案数。
枚举选取的数的个数 \(i\)，则接下来要在 \(i\) 个数中选 \(n-i\) 个数 \(+1\)，方案为 \(\dbinom{i}{n-i}\)。
于是 \(f_{n+1}=\sum\limits_{i=0}^n \dbinom{i}{n-i}=\sum\limits_{i=0}^n \dbinom{n-i}{i}\)。
子集和为 \(m\) 倍数问题
求 \(1\sim n\) 有多少个子集和为 \(m\) 倍数。
参考P10084。
数论函数估计
试估计：\(f(n)=\prod\limits_{p\le n,p\in\mathbb{P}} \dfrac{p}{p-1}\) 的大小。
注：下文 \(\log\) 一般看做 \(\ln\)，一般把 \(C\) 看做常数。
做法 \(1\)：
\(f(n)=\exp\left(\sum\limits_{p\le n,p\in\mathbb{P}} \ln\left(1+\frac{1}{p-1}\right)\right)\le \exp\left(\sum\limits_{p\le n,p\in\mathbb{P}} \frac{1}{p-1}\right)\)。
有个结论：素数倒数和估计成 \(\log\log n\) 的常数为 \(1\)，即 \(\sum\limits_{p\le n,p\in\mathbb{P}} \dfrac{1}{p}\le \log\log n+O(1)\)，证明请查阅链接。
注意到：\(\sum\limits_{p\le n,p\in\mathbb{P}} \frac{1}{p-1}-\frac{1}{p}\le \sum\limits_{i=2}^{n} \dfrac{1}{i-1}-\dfrac{1}{i}\le 1\)，于是 \(\sum\limits_{p\le n,p\in\mathbb{P}} \dfrac{1}{p-1}\le \log\log n+O(1)\)。
于是 \(f(n)\le \exp(\log\log(n)+O(1))=O(\log n)\)。
做法 \(2\)：
注意到 \(f\) 的形式和 \(\varphi\) 很像。令 \(N=\prod\limits_{p\le n,p\in\mathbb{P}} p\)，则 \(f(n)=\dfrac{N}{\varphi(N)}\)。
考虑有结论：存在常数 \(C\)，使得：\(\dfrac{n}{\varphi(n)}\le C\times \log\log n\)。
又有经典结论：\(\prod\limits_{p\le n,p\in\mathbb{P}} p\le 4^{n-1}\)，证明请查阅链接中的「关于质数积的上界估计」。
于是 \(f(n)=\dfrac{N}{\varphi(N)}\le C\times \log\log N\le C\times \log\log {4^n}=O(\log n)\)。
清零（概率期望）
给定 \(n\)，初始 \(cnt=0\)。每次扔硬币，正面就 \(cnt\gets 0\)，反面就 \(cnt\gets cnt+1\)，期望扔几次能 \(cnt=n\)。
做法：设 \(\mathbb{E}_n\) 表示 \(n\) 时的期望，初始 \(\mathbb{E}_0=0\)。
考虑每次通过 \(\mathbb{E}_{n-1}\) 步到达 \(cnt=n-1\) 后会咋样。
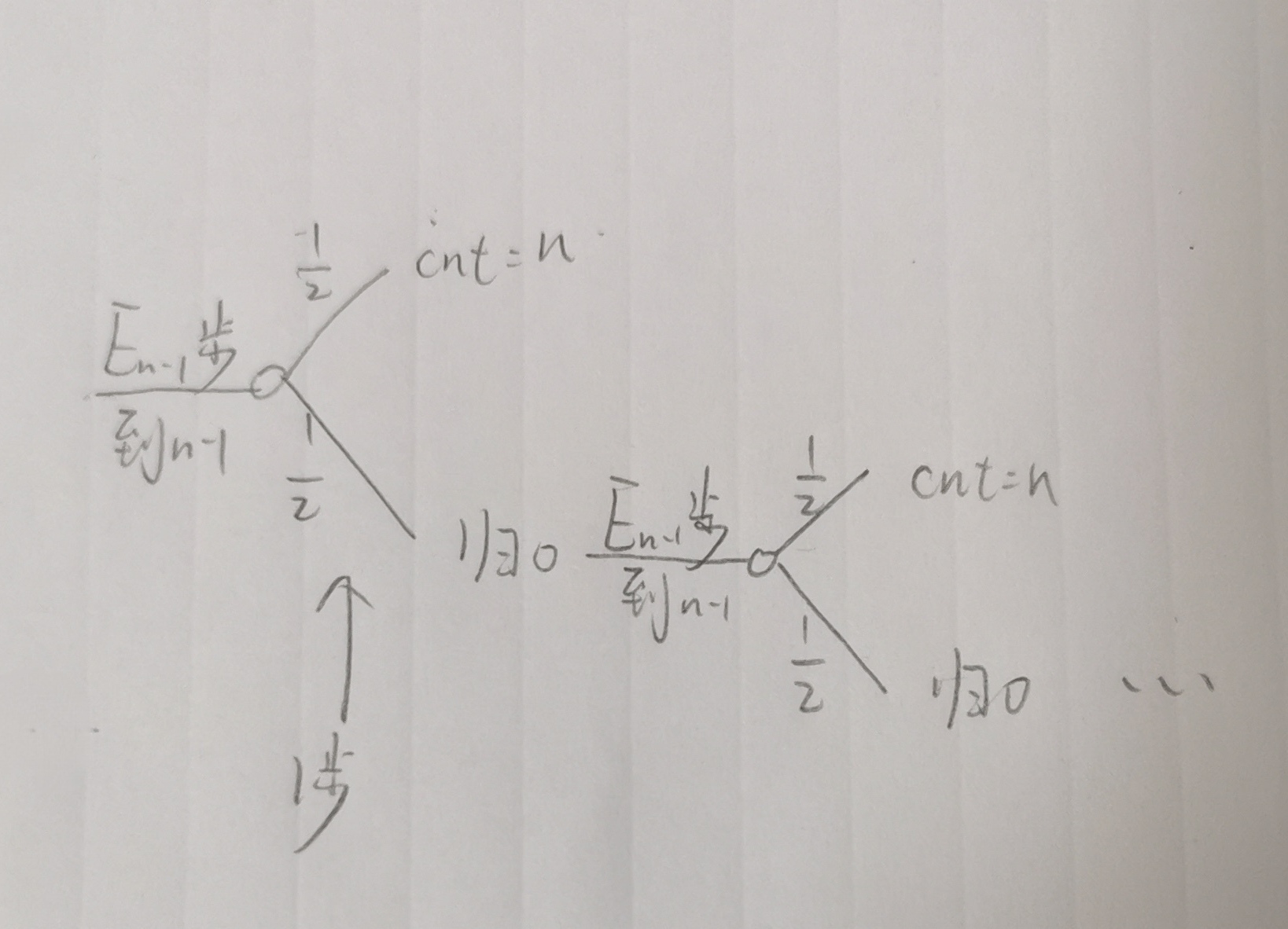
写成式子：\(\mathbb{E}_n=\sum\limits_{k\ge 1} \dfrac{k(\mathbb{E}_{n-1}+1)}{2^k}=2(\mathbb{E}_{n-1}+1)\)。于是得出 \(\mathbb{E}_{n}=2^{n+1}-2\)。
喵喵差分
设 \(m\in\N^*,n\) 为任意实数。求证：$\sum\limits_{i=0}^{m} (-1)^{m-i} \dbinom{m}{i} (n+i)^m=m! $，其中不妨定义 \(0^0=1\)。
浓组合味做法
设 \(f\) 是一个 \(\deg=n\) 的多项式，且 \(f\) 的定义域为 \([0,n]\cap\N\) 。
定义 \(f\) 的离散导数 \(\Delta f(x)=f(x+1)-f(x)(0\le x\le n-1)\)，也记作 \(\Delta ^1f(x)\)。
这时候 \(\Delta f(x)\) 只有 \(n\) 个点值，为一个 \(\deg =n-1\) 的多项式。也就是说每一次离散求导，$\deg $ 减少 \(1\)。
\(\Delta^k f(x)=\Delta(\Delta^{k-1}f(x))(k\in\N^*,k\le n)\)。
注意到：\(\Delta^k f(x)=\sum\limits_{i=0}^k (-1)^{k-i}\dbinom{k}{i} f(x+i)\)。
考虑代入 \(k=m,f(x)=x^m\)。则 \(\Delta^m f(x)=\sum\limits_{i=0}^{m} (-1)^{m-i} \dbinom{m}{i} (x+i)^m\)。
此时 \(\Delta^m f(x)\) 应为一个 \(\deg=0\) 的常数多项式，也证明了 \(\texttt{LHS}\) 的取值与 \(n\) 无关，此时只需证明 \(\Delta^m f(x)=m!\) 即可。
考虑归纳，设 \(m\) 时满足条件，\(m=0\) 时显然。考虑 \(f(x)=x^{m+1}\) 时的 \(\Delta^{m+1} f(x)\)。
\(\Delta^{m+1} f(x)=\Delta^{m}(f(x+1)-f(x))=\Delta^{m}\left(\sum\limits_{i=0}^{m}\dbinom{m+1}{i}x^i\right)=\Delta^{m}\left((m+1)x^m+\sum\limits_{i=0}^{m-1}\dbinom{m+1}{i}x^i\right)\)。
注意到离散导数的线性型，即 \(\Delta^k (f(x)+g(x))=\Delta^k f(x)+\Delta^k g(x),\Delta^k cf(x)=c\Delta^k f(x)\)。
于是 \(\Delta^{m+1} f(x)=(m+1)\Delta^{m}(x^m)+\Delta^{m}\left(\sum\limits_{i=0}^{m-1}\dbinom{m+1}{i}x^i\right)\)。由于后半部分 \(\deg<m\)，于是 \(\Delta^{m}\) 之后为 \(0\)。
代入归纳假设：\(\Delta^{m+1} f(x)=(m+1)\Delta^{m}(x^m)=(m+1)!\)。
代数组合杂交
由上文，\(\texttt{LHS}\) 的取值与 \(n\) 无关。代入 \(n=0\)：
\(\texttt{LHS}=\sum\limits_{i=0}^{m} (-1)^{m-i} \dbinom{m}{i} i^m=m!\sum\limits_{i=0}^{m} \dfrac{(-1)^{m-i}i^m}{i!(m-i)!}\)。
注意到斯特林数的通项公式为：\(\displaystyle{n\brace m}=\sum\limits_{i=0}^m \dfrac{(-1)^{m-i}i^n}{i!(m-i)!}\)。
于是 \(\texttt{LHS}=m!\displaystyle{m\brace m}=m!\)。
代数推导保平安
在不知道离散导数相关知识的情况下呢？
\(\begin{aligned} \sum\limits_{i=0}^{m} (-1)^{m-i} \dbinom{m}{i} (n+i)^m&=\sum\limits_{i=0}^{m} (-1)^{m-i} \dbinom{m}{i} \sum\limits_{j=0}^m\dbinom{m}{j}n^{m-j}i^j \\ &=\sum\limits_{j=0}^m\dbinom{m}{j}n^{m-j}\sum\limits_{i=0}^{m} (-1)^{m-i} \dbinom{m}{i} i^j\\ &=m!\sum\limits_{j=0}^m\dbinom{m}{j}n^{m-j}\sum\limits_{i=0}^m \dfrac{(-1)^{m-i}i^j}{i!(m-i)!}\\ &=m!\sum\limits_{j=0}^m\dbinom{m}{j}n^{m-j}\displaystyle{j\brace m} \end{aligned}\)
由于斯特林数的性质，当 \(n<m\) 时，\(\displaystyle{n\brace m}=0\)，\(\displaystyle{m\brace m}=1\)。于是 \(\texttt{LHS}=m!\dbinom{m}{m}n^{m-m}=m!\)。
关于 \(n\) 个 \([0,1]\) 的随机变量第 \(k\) 小的期望值
结论：对于 \(n\) 个取值范围为 \([0,1]\) 的随机变量 \(x_{1,2,\cdots ,n}\)，其中 \(k\) 小值的期望为 \(\dfrac{k}{n+1}\)。
暴力微积分
枚举 \(k\) 小值位置，其可能是 \(n\) 个中任意一个。然后再枚举 \(<\) 这个值的分部情况，有 \(\dbinom{n-1}{k-1}\) 种方案。
然后枚举 \(k\) 小值 \(x\) 积分，小于 \(k\) 小值部分为 \(x^{k-1}\)，大于的部分为 \((1-x)^{n-k}\)，然后对期望有 \(x\) 的贡献。
于是 \(ans=n\dbinom{n-1}{k-1}{\displaystyle \int}_0^1 x^{k-1}(1-x)^{n-k} x{\rm d}x=n\dbinom{n-1}{k-1}\Beta(k+1,n-k+1)\)。
根据贝塔函数的性质，有：\(\Beta(p,q)=\dfrac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}\)，\(\Gamma(n)=(n-1)!\)。
于是 \(ans=n\times \dfrac{(n-1)!}{(k-1)!(n-k)!}\times \dfrac{k!(n-k)!}{(n+1)!}=\dfrac{k}{n+1}\)。
组合意义毁天灭地
不妨考虑引入第 \(n+1\) 个随机变量，注意到分布均匀性，且取值是 \([0,1]\)。
所以可以认为第 \(k\) 小的变量的期望等于第 \(n+1\) 个变量小于等于第 \(k\) 小的变量的概率。
那么问题就变为了如何求这个概率，考虑统计方案数。
他们的大小关系一共有 \((n+1)!\) 种，而 \(n+1\) 个变量小于等于第 \(k\) 个变量的方案数一共有 \(k\times n!\)。因为第 \(n+1\) 个变量一共有 \(k\) 个位置可以插入。
所以概率为 \(\dfrac{k}{n+1}\)，也就是第 \(k\) 小的期望。
小清新概率期望
初始 \(s=0\)，每次操作随机选取一个 \([0,1]\) 内实数 \(x\)，\(s\gets s+x\)，求使得 \(s>1\) 的期望操作次数。
做法：\(\mathbb{E}(X)=\sum\limits_{k\ge 0} \mathbb{P}(X>k)\)，于是转化成求 \(\mathbb{P}(X>k)\)，即 \(k\) 次操作后仍然 \(s\le 1\) 的概率。
设 \(p_n(x)\) 表示 \(n\) 次操作后 \(s\le x\) 的概率，则有 \(p_0(x)=1,p_n(x)={\displaystyle\int}_0^x p_{n-1}(t)\ \mathbb{d} t\)。
于是容易归纳证明：\(p_n(x)=\dfrac{1}{n!}x^n\Rightarrow \mathbb{P}(X>k)=p_k(1)=\dfrac{1}{k!}\)。
于是 \(\mathbb{E}(X)=\sum\limits_{k\ge 0}\frac{1}{k!}=e\)。
收敛的调和
求 \(s=\sum\limits_{n=0}^{\infty} \dfrac{(-1)^n}{n+1}\) 的值。
做法：考虑 \({\displaystyle\int} \dfrac{1}{1+x}\mathbb{d}x=\ln(1+x)\)。
又：\({\displaystyle\int} \dfrac{1}{1+x}\mathbb{d}x={\displaystyle\int} \sum\limits_{n=0}^{\infty} (-x)^n \mathbb{d}x=\sum\limits_{n=0}^{\infty} \dfrac{(-1)^nx^{n+1}}{n+1}\)，其中 \(-1<x\le 1\)。
带入 \(x=1\) 即得：\(s=\ln 2\)。
