基于 dfs 的若干树上颜色相关路径计数问题

下面解法存在借鉴。

ABC163F

考虑求不满足条件的路径树，发现与割掉这个颜色形成的连通块大小相关。

我们设 \(cnt_i\) 表示我们在树上已经 dfs 枚举到的过程中，所有颜色为 \(i\) 的子树的总大小（如果有包含，记录 \(\max\)）。

对每个点子树内统计贡献。找到每一个颜色相同的，间隔的点两两可以形成不包含该颜色的路径，用总方案数减去这些方案数即可。

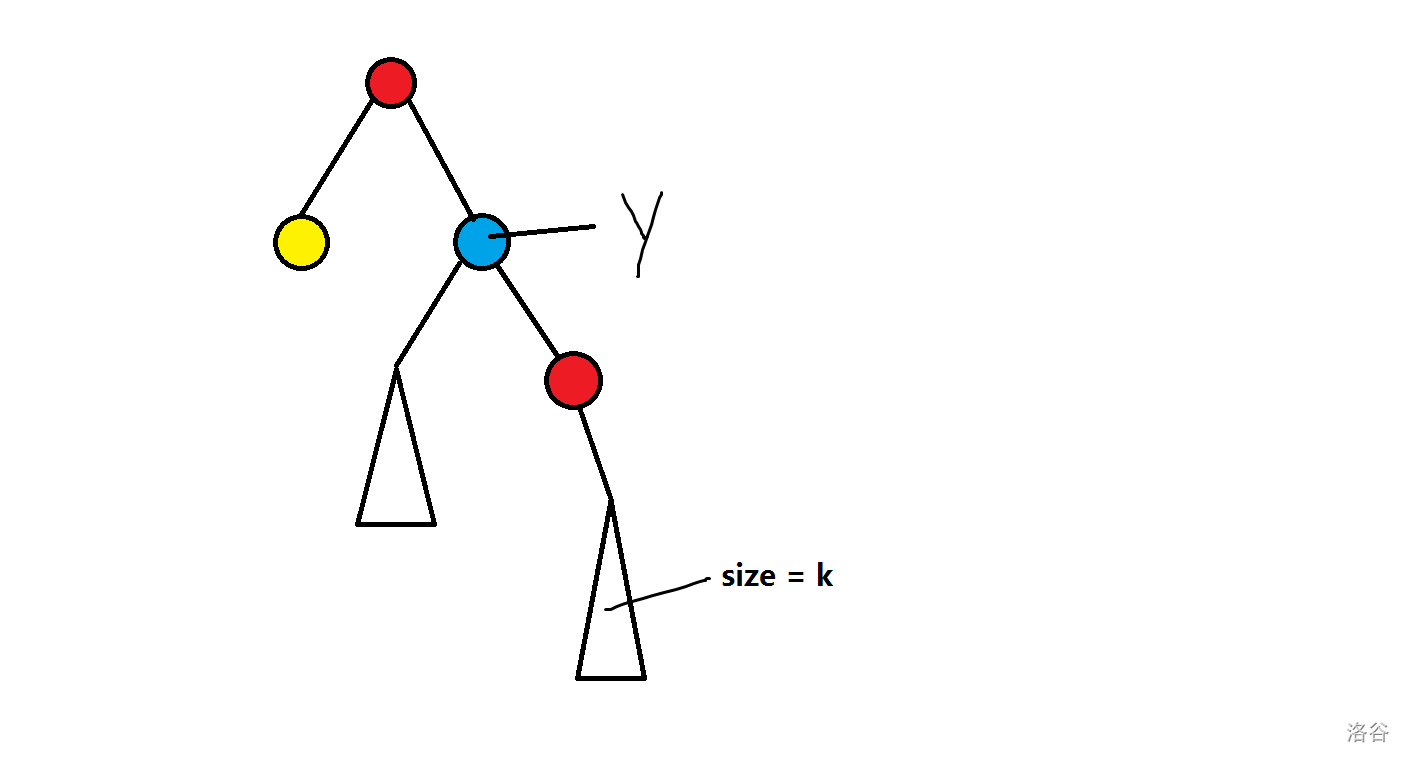
例如此时，考虑红色，\(y\) 对 \(x\) 的贡献为 \(siz_y-k\)，只需求 \(k\)。

令 \(C=c_x\)，我们在做 \(y\) 之前存下 \(cnt'_C\)，表示 \(y\) 之前 dfs 时所有颜色为 \(C\) 的子树的总大小（如果有包含，记录 \(\max\)）。然做下面的红色节点后在记一个 \(cnt_C\)，那么 \(k=cnt_C-cnt'_C\)。

同时要对根处在处理一下，具体细节看代码，线性还是太妙了。

CF1923E

考虑对一条路径 \((u,v)\) 在 dfs 序更大的点 \(v\) 处算贡献。

同样记 \(cnt_i\) 表示到当前点时颜色 \(i\) 应该算的贡献大小。考虑做到点 \(x\)，此时依次做如下操作：

• 把除了 \(1\to x\) 路径外之前 dfs 过的点累加到 \(cnt\) 中对应颜色。

• 遍历 \(1\to x\) 路径，把路径上的每个颜色 \(cnt\) 值更改为 \(1\)。

• 计算 \(x\) 点贡献，即 \(ans\gets cnt_{c_x}\)。

动态地在 dfs 时维护此过程即可。具体细节看代码。

CF1681F

就是上面第一题的点颜色改成边颜色。

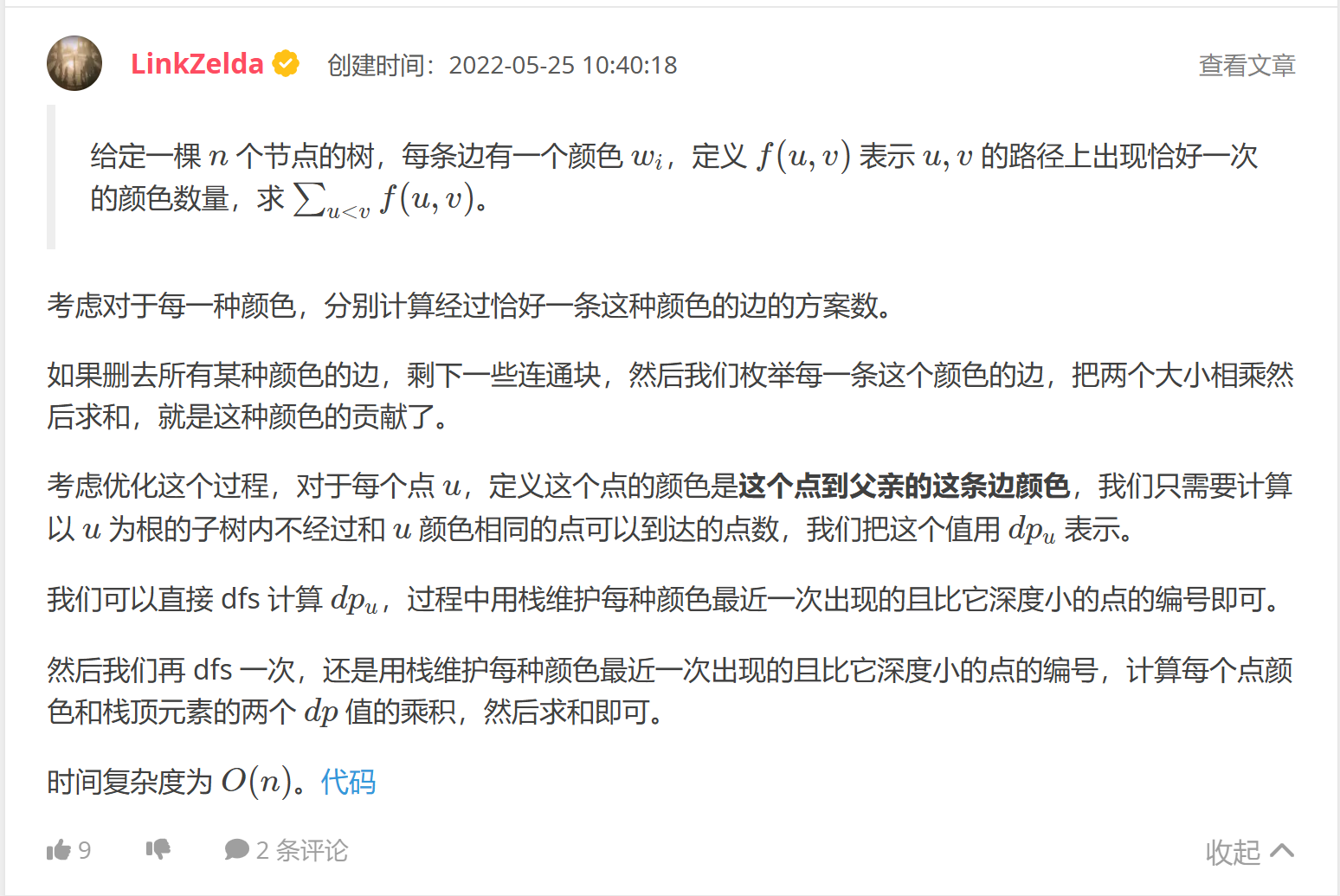
学不会！学不会！可能这种能也替代点权的做法，但是我！学！不！会！摆了。代码。