竞赛图性质研究(强联通分量/哈密顿回路)
前置知识#
竞赛图,强联通分量,哈密顿回路的定义。
定义点 的入读为 。
强联通分量相关#
结论 1#
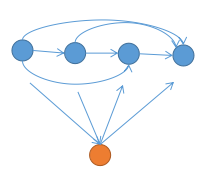
竞赛图强连通缩点后的 呈链状,并且前面的所有点向后面的所有点连边,下图中每个圆块为原图的一个强联通分量。
证明:考虑归纳,逐强连通块加入。设目前有一条链,插入一个新连通块 。
如果 连向所有点,放在链头;如果所有点连向 ,放在链尾。
否则 的出边一定都在 的入边的后边(否则成环)。
找到分界点,把 插在中间即可。
结论 2#
在竞赛图中,如果存在路径 却不存在路径 ,即 所在的强联通分量的拓扑序严格小于 的,则 。
证明:设 所在的强联通分量为 。考虑缩点后 的“链”,设链内包含的所有点构成集合 。
由于不存在路径 ,所以 ,且由于是竞赛图,于是 ,存在 的有向边,于是 。
由于 外的点显然与 没有连边,而且 ,于是 。
结论 3#
已知竞赛图所有点的 ,则可以确定每个强联通分量内包含的点。
证明:考虑按某种拓扑序遍历所有强联通分量,设遍历到的前若干个强联通分量里的所有点构成的集合为 ,则 。因为按拓扑序,后遍历的点一定不能与先遍历的点连边。
考虑把所有点按 升序排序成序列 ,由于结论 此时顺序遍历可以类比为拓扑序中顺序遍历。此时若 ,此时产生了一个新的强联通分量拓扑序遍历前缀。
考虑上一个满足条件的是 ,初始 。则 构成了一个新的强联通分量。由于拓扑序这样显然是不重不漏的。
哈密顿回路/路径相关#
结论1#
任意竞赛图存在一条哈密顿路径。
结论2#
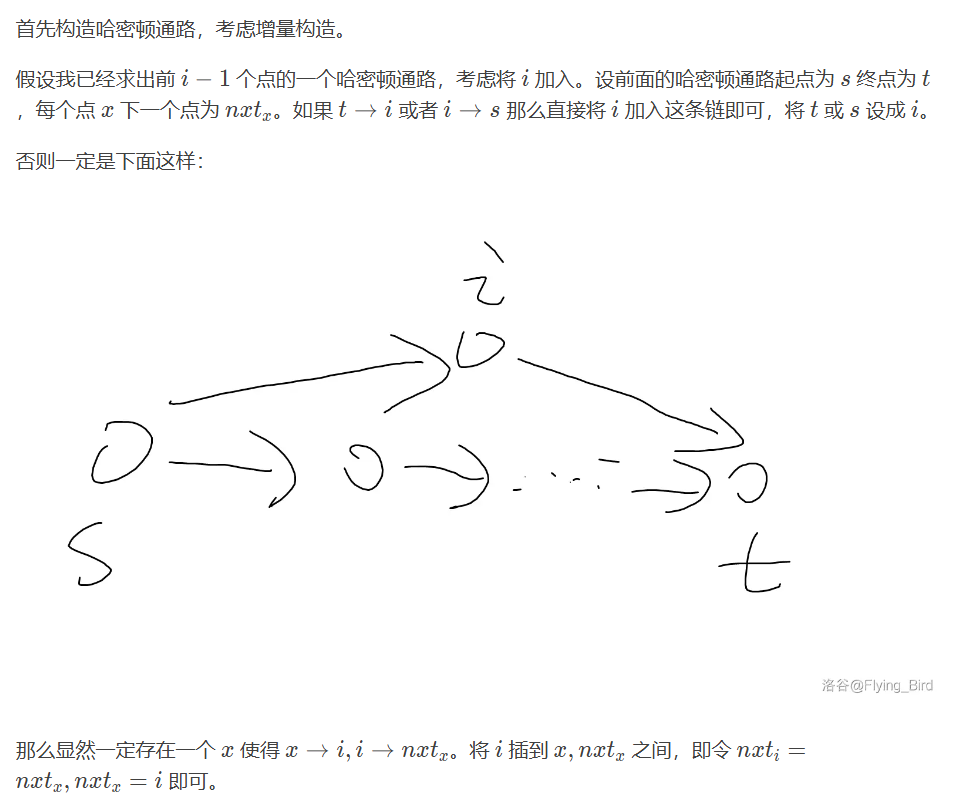
任意强联通的竞赛图存在哈密顿回路,考虑构造性证明。
归纳,首先如上构造出一条哈密顿路径。由于强联通性,此时能找到一个点连向起点,于是构造出一个小哈密顿回路,考虑逐步扩展。
首先如果又往后找到了一个连向起点 的点,直接扩展过去即可,如下图:
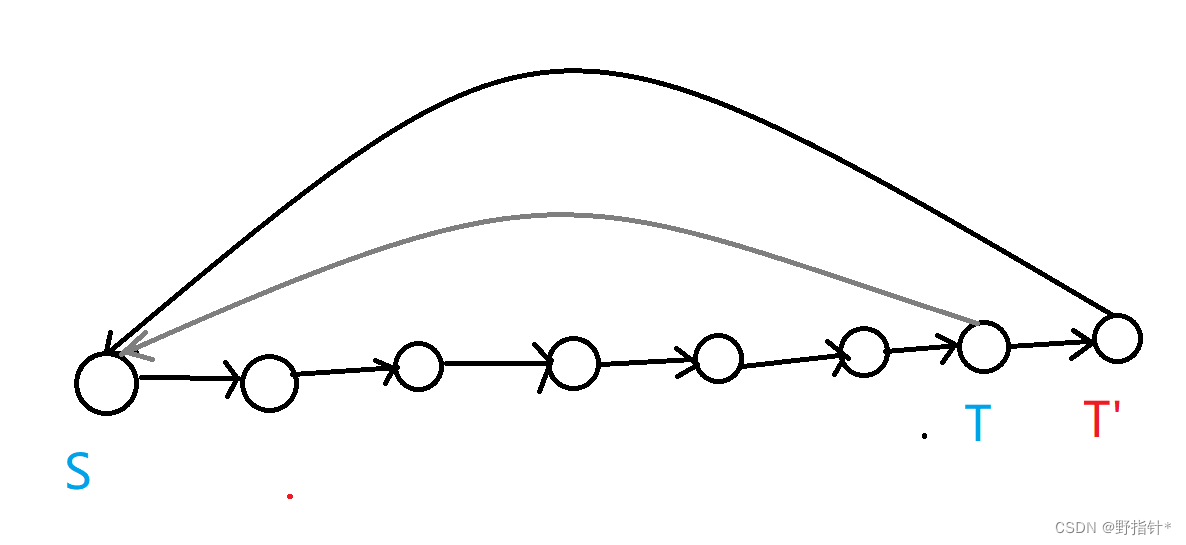
否则考虑 路径上第一个点 ,使得当前 往后存在一个点连向 。记 前面那个点为 ,由于 是第一,于是下图中边 的边存在。
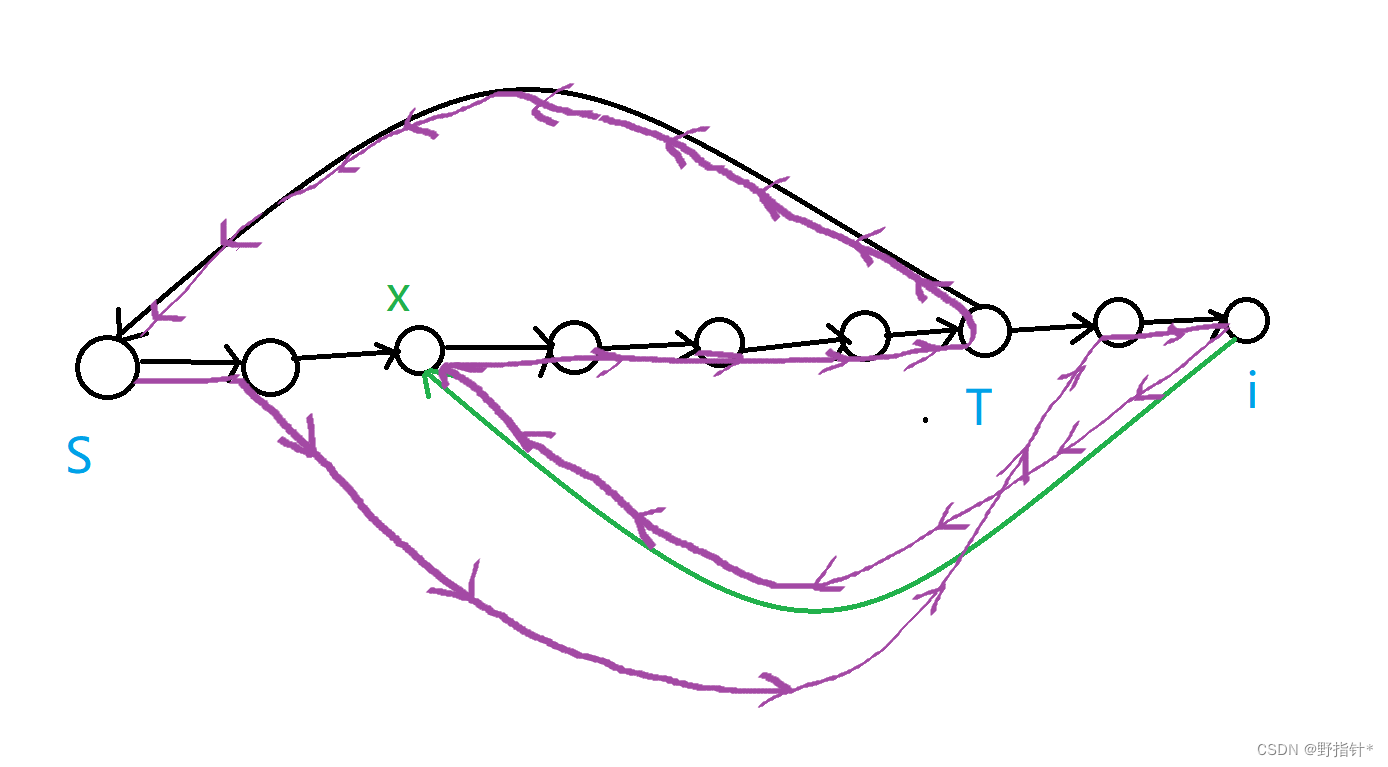
于是构造了 的新哈密顿回路。注意此时 为起点, 为终点。由于强联通性能一直构造下去直到包含所有点。
例题#
-
CF1779E。注意到能留下的点等价于这个点能游走经过所有点,等价与这个点在竞赛图缩点的链头强联通分量中。
要按上述方法找出这个强联通分量,只需确定所有点的 ,每次询问除了这个点的其他所有点,得到这个点的 ,则 ,。 -
CF1498E。这题不需要询问。发现给定了竞赛图每个点的 ,于是确定了所有强联通分量,每次求 取个最大值就知道题目所求的极差了。
-
P3561。首先按上文结论 直接找出所有强联通块,然后按上文对每个强联通块找出哈密顿回路,由于缩点后的形状之后随便做即可。有点难写。
的
#include<bits/stdc++.h>
#define LL long long
#define bs basic_string<int>
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2e3+5;
int n,m,b[N],p[N],in[N],w[N],to[N],mx[N];bool a[N][N];
bs ans[N],rg[N],g,h,H;
inline void add(int u,int v){a[u][v]=1;in[v]++;}
inline void upd(bs &f,int x,int y)
{
bs g;for(int i=0;i<=x;i++) g+=f[i];g+=y;
for(int i=x+1;i<f.size();i++) g+=f[i];f=g;
}
inline void check()
{
for(int i=1;i<=n;i++)
{
int len=ans[i].size();
for(int j=0;j<len-1;j++)
{
int k=ans[i][j],l=ans[i][(j+1)%len];
if(!a[k][l]){cout<<"No\n"<<i<<" "<<k<<" "<<l;exit(0);}
}
}cout<<"Yes\n";
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;
for(int i=2;i<=n;i++) for(int j=1,o;j<i;j++) cin>>o,o?add(j,i):add(i,j);
iota(p+1,p+1+n,1);sort(p+1,p+1+n,[](int x,int y){return in[x]<in[y];});
for(int i=1,s=0,t;i<=n;i++)
{
t=p[i],s+=in[t];
if(s==i*(i-1)/2) b[++m]=i;
}
for(int i=1;i<=m;i++)
{
int l=b[i-1]+1,r=b[i];g.clear();
if(l==r){rg[i]+=p[l];continue;}g+=p[l];g+=p[l+1];
if(!a[p[l]][p[l+1]]) swap(g[0],g[1]);
for(int j=l+2;j<=r;j++)
{
int w=p[j],s=g[0],t=g.back();
if(a[w][s]) upd(g,-1,w);
else if(a[t][w]) g.push_back(w);
else
{
int W=-1;
for(int k=0;k<g.size();k++) if(a[g[k]][w]) W=k;
upd(g,W,w);
}
}
memset(to,-1,sizeof(to));memset(mx,-1,sizeof(mx));
for(int j=0;j<g.size();j++) to[g[j]]=j;
for(int j:g) for(int k=1;k<=n;k++) if(a[k][j]) mx[j]=max(mx[j],to[k]);
h.clear();int w=0;
for(int j=0;j<g.size();j++)
{
h+=g[j];
if(a[g[j]][g[0]]){w=j;break;}
}
while(w!=g.size()-1)
{
int W=0;
for(int j=0;j<h.size();j++) if(mx[h[j]]>w){W=j;break;}
int r=mx[h[W]];H.clear();
for(int j=W;j<h.size();j++) H+=h[j];
for(int j=0;j<W;j++) H+=h[j];
for(int j=w+1;j<=r;j++) H+=g[j];w=r;h=H;
}
rg[i]=h;
}
for(int i=1;i<=m;i++)
{
int l=b[i-1]+1,r=b[i],len=r-l+1;g=rg[i];
for(int j=0;j<len;j++) w[g[j]]=j;
for(int j=l;j<=r;j++)
{
int t=p[j],w=::w[t];
for(int k=0;k<len;k++,w++,(w==len)&&(w=0)) ans[t]+=g[w];
for(int k=i+1;k<=m;k++) for(int l:rg[k]) ans[t]+=l;
}
}
// check();
for(int i=1;i<=n;i++){cout<<ans[i].size()<<" ";for(int j:ans[i]) cout<<j<<" ";cout<<"\n";}
return 0;
}
一种特殊竞赛图的性质#
例题:CF1338E。请自行阅读题解。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】