P8820(csp-s 2022 T4)题解
背景
解法
一眼 \(\texttt{ddp}\) ,没话说。下面假设树以 \(1\) 为根。一次传输称作从一个点跳到另一个点。设询问的两个点为 \(u,v\),\(x\) 点的权值为 \(c_x\)。
\(k=1\)
问题转化为求一条路径的权值和。(这是显然的) 记 \(s_i\) 表示 \(i\) 到根的路径上的权值和。则答案为:\(\large s_u+s_v-s_{\text{lca}}-s_{fa_{\text{lca}}}\)。
\(k=2\)
跳跃方式最优显然是:

即每次往上跳 \(1\) 或 \(2\) 步。设已经跳到 \(x\) 点,上一个点(路径上 \(x\) 的儿子)是点 \(y\)。
\(f_{x,0/1}\) 表示跳到 \(x\) 的 路径上的儿子\(/\)孙子最小答案。
\(\begin{cases} f_{x,0}=\min\{f_{y,0}+c_x,f_{y,1}+c_x\}\\ f_{x,1}=f_{y,0} \end{cases}\)
写成矩阵转移:\([f_{y,0},f_{y,1}]\times\begin{bmatrix} c_x & +\infty\\ c_x & 0 \end{bmatrix}=[f_{x,0},f_{x,1}]\)。
这里(下面也是)矩阵乘法 \(A\times B=C\) 满足 \(C_{i,j}=\min\{A_{i,k}+B_{k,j}\}\)。容易得到这种矩阵乘法没有交换律,有结合律。
先从 \(fa_u\) 一直向上转移到 \(\text{lca}\) 再从 \(\text{lca}\) 一直向下转移到 \(v\),用矩阵转移。
在最前面乘上 \(\begin{bmatrix} c_u & +\infty\\ +\infty & +\infty \end{bmatrix}\)(相当于初始 \([f_{u,0},f_{u,1}]=[c_u,+\infty]\)),得到的矩阵第一行第一列(即 \(f_{v,0}\))就是答案。处理 \(u\) 往上跳和 \(\text{lca}\) 往下跳用倍增即可。
\(k=3\)
记 \(f_{x,0/1/2}\) 表示跳到距离 \(x\) 点 \(0/1/2\) 的最小答案。已经跳到 \(x\),上一个点是 \(y\)。
每次距离为 \(1\) 时可以是这个点的父亲,这个点在路径上的儿子,这个点的其他儿子(都有可能会转移)。
距离为 \(2\) 时可能是这个点路径上的孙子,这个点路径上的儿子的其他所有儿子(其他情况都一定不优)。
有:\(\begin{cases} f_{x,0}=\min\{f_{y,0}+c_x,f_{y,1}+c_x,f_{y,2}+c_x\}\\ f_{x,1}=\min\{f_{y,0},f_{y,1}+c'_x\}\\ f_{x,2}=f_{y,1} \end{cases}\),这里 \(c'_x\) 表示所有距离 \(x\) 为 \(1\) 的点中 \(c\) 值的最小值。
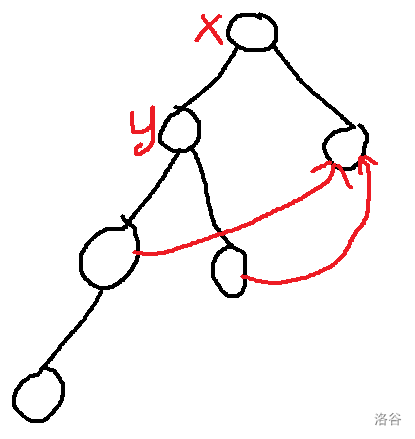
距离 \(x\) 为 \(1\) 的点可能通过红线跳过去,于是就有了 \(f_{y,1}+c'_x\)。
还有一个问题:如果 \(f_{y,1}\) 最终是在 \(y\) 的父亲那不是 \(f_{x,1},f_{x,2}\) 的转移都不成立了吗?
考虑到这样转移到 \(f_{x,1},f_{x,2}\) 显然都不是最优的跳跃方案,对答案没有贡献,即使转移了也没关系。而最优的方案都被转移了,保证了答案的正确性。
转移写成矩阵:\([f_{y,0},f_{y,1},f_{y,2}]\times\begin{bmatrix} c_x & 0&+\infty\\ c_x & c'_x&0\\ c_x & +\infty&+\infty \end{bmatrix}=[f_{x,0},f_{x,1},f_{x,2}]\)。同上倍增维护即可。
\(\text{code}\),可以参考一下这里倍增跳的实现方法:
#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=2e5+5;const LL inf=1e18;
int n,m,K,tot,head[N],d[N],w[N],w1[N],fa[N][25];
LL s[N];
struct edge{int to,nex;}e[N<<1];
inline void add(int u,int v)
{
e[++tot]={v,head[u]};head[u]=tot;
e[++tot]={u,head[v]};head[v]=tot;
}
struct jz
{
LL a[3][3];
jz(){memset(a,0,sizeof(a));}
inline LL* operator[](int x){return a[x];}
inline void E(){for(int i=0;i<K;i++) for(int j=0;j<K;j++) a[i][j]=(i==j)?0:inf;}
}b[N][25][2];
inline jz A(LL x)
{
jz z;
if(K==2) z[1][1]=inf,z[0][1]=0,z[0][0]=z[1][0]=w[x];
else z[0][2]=z[2][1]=z[2][2]=inf,z[0][1]=z[1][2]=0,
z[0][0]=z[1][0]=z[2][0]=w[x],z[1][1]=w1[x];return z;
}
inline jz operator*(jz x,jz y)
{
jz z;
for(int i=0;i<K;i++) for(int j=0;j<K;j++) z[i][j]=inf;
for(int i=0;i<K;i++) for(int j=0;j<K;j++)
for(int k=0;k<K;k++) z[i][j]=min(z[i][j],x[i][k]+y[k][j]);
return z;
}
void dfs(int th,int f)
{
d[th]=d[f]+1;fa[th][0]=f;w1[th]=w[f];
for(int i=1;i<=20;i++) fa[th][i]=fa[fa[th][i-1]][i-1];
if(K==1) s[th]=s[f]+w[th];
for(int i=head[th];i;i=e[i].nex)
{
int to=e[i].to;
if(to!=f) dfs(to,th),w1[th]=min(w1[th],w[to]);
}
}
inline int lca(int u,int v)
{
if(d[u]<d[v]) swap(u,v);
int t=d[u]-d[v];
for(int i=0;t;t>>=1,i++) if(t&1) u=fa[u][i];
if(u==v) return u;
for(int i=20;i>=0;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
inline jz Ju(int x,int L,int o)
{
x=fa[x][0];int t=d[x]-d[L];jz z;z.E();
for(int i=0;t>0;t>>=1,i++) if(t&1) z=(!o)?(z*b[x][i][0]):(b[x][i][1]*z),x=fa[x][i];
return z;
}
inline LL slo(int u,int v)
{
int L=lca(u,v);
if(K==1) return s[u]+s[v]-s[L]-s[fa[L][0]];if(d[u]<d[v]) swap(u,v);
jz y;y.E();y[0][0]=w[u],y[1][1]=y[2][2]=inf;
jz z=(v==L)?(y*Ju(u,v,0)*A(v)):(y*Ju(u,L,0)*A(L)*Ju(v,L,1)*A(v));
return z[0][0];
}
int main()
{
// fr(transmit)
scanf("%d%d%d",&n,&m,&K);int u,v;
for(int i=1;i<=n;i++) scanf("%d",&w[i]);w[0]=1e9+7;
for(int i=1;i<n;i++) scanf("%d%d",&u,&v),add(u,v);
dfs(1,0);
if(K>=2)
{
for(int i=1;i<=n;i++) b[i][0][0]=b[i][0][1]=A(i);
for(int j=1;j<=20;j++) for(int i=1;i<=n;i++)
b[i][j][0]=b[i][j-1][0]*b[fa[i][j-1]][j-1][0],b[i][j][1]=b[fa[i][j-1]][j-1][1]*b[i][j-1][1];
}
while(m--) scanf("%d%d",&u,&v),printf("%lld\n",slo(u,v));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号