ABC134F 题解

\(\text{link}\) 。难想的 \(\texttt{dp}\) 。下面用 \(m\) 来表示题目中的 \(k\)，因为 \(\texttt{dp}\) 时会用到 \(k\)。

我们把左侧放 \(n\) 个球，右侧放 \(n\) 个箱子，则 \(|i-p_i|\) 等于第 \(i\) 个球与第 \(p_i\) 个盒子的连线（下面记作 \(i\to p_i\)）与水平线（两球中间与两箱子中间的连线）的交点。画个图解释一下：

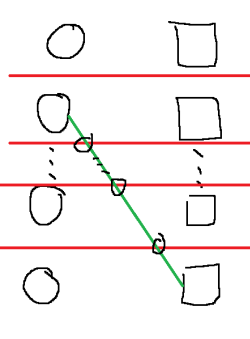（左边是球，右边是箱子，绿色是 \(i\to p_i\) 的连线，红色是水平线，黑圈是交点）

---

下面设 \(f_{i,j,k}\) 表示考虑第 \(i\) 个球以前水平线对怪异度的贡献，这时还有 \(j\) 个球和盒子没有配对，当前的怪异度为 \(k\) 的方案数。

为了好转移，我们把水平线对怪异度的贡献这样定义：如果统计到了某条水平线，这时还有 \(j\) 个球和盒子没有配对，则水平线对答案的贡献为 \(2j\)。

因为这时 \(j\) 个球会往后连线，经过这个水平线，有 \(j\) 的贡献。\(j\) 个盒子会往后连线，经过这个水平线，有 \(j\) 的贡献。所以贡献为 \(2j\)。而且最终的答案就是 \(f_{n,0,m}\)。初值为 \(f_{0,0,0}=1\) 。

先亮一下转移：\(f_{i,j,k}=f_{i-1,j-1,k-2j}+(2j+1)f_{i-1,j,k-2j}+(j+1)^2f_{i-1,j+1,k-2j}\)。

下面解释一下等号右边的 \(3\) 个加数。设做到 \(i-1\) 时未匹配的个数为 \(J\)。

1. 如果第 \(i\) 个球和第 \(i\) 个盒子啥都不做的话，此时有一种可能，且 \(J=j-1\)。所以方案数为 \(f_{i-1,j-1,k-2j}\).
2. 如果第 \(i\) 个球和第 \(i\) 个盒子恰有一个和之前 \(J\) 个未匹配的盒子（或球）匹配，那么此时有 \(2j\) 种可能，且 \(J=j\)。所以方案数为 \(2jf_{i-1,j,k-2j}\).
   如果第 \(i\) 个球和第 \(i\) 个盒子之间连线，则此时有一种可能，方案数也为 \(f_{i-1,j,k-2j}\)，所以第二种情况共贡献了 \((2j+1)f_{i-1,j,k-2j}\) 的方案数。
3. 如果第 \(i\) 个球和第 \(i\) 个盒子都和之前 \(J\) 个未匹配的盒子（或球）匹配，那么此时有 \(J^2\) 种可能，且 \(J=j+1\)。所以方案数为 \((j+1)^2f_{i-1,j+1,k-2j}\).

直接按此 \(\texttt{dp}\) 即可，注意若枚举到 \(j=0\) 时不能有情况 \(1\)，要特判一下。

$\texttt{code}$

#include<bits/stdc++.h>
#define LL long long
#define fr(x) freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);
using namespace std;
const int N=55,M=2505,mod=1e9+7;
int n,m,f[N][N][M];
int main()
{
	scanf("%d%d",&n,&m);if(m&1) return 0*puts("0");f[0][0][0]=1;
	for(int i=1;i<=n;i++) for(int j=0;j<=i;j++) for(int k=2*j;k<=m;k+=2)
		f[i][j][k]=(1ll*(j+1)*(j+1)*f[i-1][j+1][k-2*j]+1ll*(2*j+1)*f[i-1][j][k-2*j]+(j?f[i-1][j-1][k-2*j]:0))%mod;
	printf("%d",f[n][0][m]);
	return 0;
}