动态规划算法三：0-1背包问题
一、算法分析
1、问题描述：给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问:应如何选择装入背包的物品，使得装入背包中物品的总价值最大？
输入：集合W={w1,w2,...,wn}, V={v1,v2,...,vn}, 数值C
输出：向量X={x1,x2,...,xn}, xi=1表示物品i放入包中，xi=0表示不放入包中。Σxiwi ≤ C，且Σxivi最大
2、分析：（寻找最优子结构，转移矩阵，递归关系公式）
假设y = {y1, y2,...,yi}是W，V，数值为j的0-1背包问题的一个最优解（最优解可能不止一个）
（1）若wi > j, 则y` = {y1, y2,...,yi-1}为W={w1,w2,...,wi-1}, V={v1,v2,...,v-1}, 数值为j的子问题的最优解（yi必定为0，物品i肯定不能放入背包中）；
（2）若wi <= j, 且yi = 0，则y` = {y1, y2,...,yi-1}为W={w1,w2,...,wi-1}, V={v1,v2,...,v-1}, 数值为j的子问题的最优解（yi当前值为0，物品i经过权衡后，决定不放入背包中）；
（3）若wi <= j, 且yi = 1，则y` = {y1, y2,...,yi-1}为W={w1,w2,...,wi-1}, V={v1,v2,...,v-1}, 数值为j - wi的子问题的最优解（yi当前值为1，物品i放入背包中）；
以上（1）、（2）结论，显然成立，可以用反证法证明结论（3）：
3、由以上分析，转移矩阵如下:
其中，i表示物品数量，j表示背包重量限制，m[i,j]的值表示对应场景下，背包可以装取货区的最大价值，即目标值。
4、算法步骤：
（1）数据设置：有以上分析，需要遍历物品数量与背包重量，用二维数组记录目标值；
（2）初始化：当数量为0或者背包重量限制为0时，目标值为0（对应转移矩阵的初始情况）；
（3）遍历i和j：根据判断条件以及历史记录，计算出新值
5、获取结果：
根据背包价值矩阵，判断物品数量变动时，目标值是否变动，以此确定该物品是否需要装入背包。
二、代码实现
1、构建背包价值矩阵：
// w表示各物品重量，v表示各物品价值，n表示物品数量，c表示背包重量限制
int *knapsack(int *w, int *v, int n, int c)
{
// 内存申请，将一维矩阵当做二维矩阵使用，行优先
int *m = (int *)malloc((n + 1) * (c + 1) * sizeof(int));
int i, j;
// 初始化
for (i = 1; i < n + 1; i++) {
m[i * (c + 1)] = 0;
}
for (j = 0; j < c + 1; j++) {
m[j] = 0;
}
// 遍历物品数量i与重量j限制，填写背包价值矩阵
// 背包矩阵中，添加了i=0和j=0时的初始值，导致m[i,j]对应的物品重量为w[i-1]，价值为v[i-1]
for (i = 1; i <= n; i++) {
for (j = 1; j <= c; j++) {
// 在填写m[i,j]时，实际上是确认第i-1各物品是否需要放入背包
// 若当前物品重量w[i-1]大于背包总体重量时，必定不能放入，目标值与分析上一个物品时的目标值(m[i-1,j])相同
m[i * (c + 1) + j] = m[(i - 1) * (c + 1) + j];
// 若当前物品重量小于背包总体重量，需要重点考虑
if (w[i - 1] <= j) {
// 若该物品的重量小于物品总体重量，且当前物品价值v[i-1] + 原放弃一个物品且保证其重量不超出时对应的目标值m[i-1,j-wi]
// > 不放入该物品是的目标值m[i,j]时，选择将该物品放入背包中，此时可以保证重量与总价值均为最优
if (v[i - 1] + m[(i - 1) * (c + 1) + j - w[i - 1]] > m[(i - 1) * (c + 1) + j]) {
// 将该物品价值v[i-1]+背包中重量减去当前物品重量时且物品个数少一个时对应的目标值，并将其更新到m[i,j]中
// 确保重量限制于物品个数限制，m中记录的均为对应场景下的最优值
m[i * (c + 1) + j] = v[i - 1] + m[(i - 1) * (c + 1) + j - w[i - 1]];
}
}
}
}
return m;
}
2、根据价值矩阵，获取结果：
// m为背包价值矩阵，n为物品数量，w为物品重量，c为背包重量限制
int *bulidSolution(int *m, int n, int *w, int c)
{
int i;
int j = c;
int *x = (int*)malloc(n * sizeof(int));
for (i = n; i >= 1; i--) {
// 判断物品个数变化时，目标值是否变化
if (m[i * (c + 1) + j] == m[(i - 1) * (c + 1) + j]) {
// 不变，该物品不放入背包
x[i - 1] = 0;
} else {
// 变化，物品放入背包，且更新背包重量j
x[i - 1] = 1;
j -= w[i - 1];
}
}
return x;
}
三、测试结果
测试程序：
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int main(void)
{
int w[] = {2, 3, 4, 5};
int v[] = {3, 4, 5, 6};
int *m, *x;
int thingsNum = sizeof(w) / sizeof(w[0]);
int maxWeight = 9;
// knapsack函数实现参考上一节内容
m = knapsack(w, v, thingsNum, maxWeight);
// 打印价值矩阵m
printf("knapsackTab start: \n\n");
for (int i = 0; i < thingsNum + 1; i++) {
for (int j = 0; j < maxWeight + 1; j++) {
printf(" %2d ", m[i * (maxWeight + 1) + j]);
}
printf("\n\n");
}
printf("knapsackTab end. \n");
// bulidSolution函数实现参考上一节内容
x = bulidSolution(m, thingsNum, w, maxWeight);
// 输出物品装包策略：0-不放，1-放入
printf("\nans[] = ");
for (int i = 0; i < thingsNum; i++) {
printf("%2d ", x[i]);
}
while (1);
return 0;
}
测试结果：
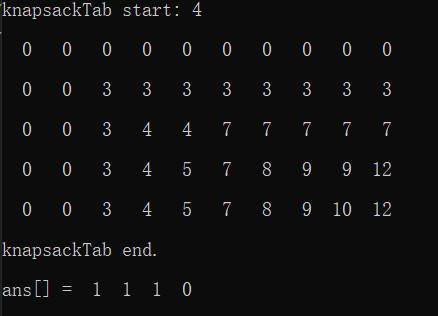
四、leetcode题
待分析
