分治算法四：堆排序

目录

• 一、算法思路
• 二、代码实现
• 三、测试结果

一、算法思路

总体思路：利用最大堆的特性——根节点为最大值，通过将根节点与数组末端元素进行交换，并对剩余元素进行调整，依次取出剩余元素最大值，完成对整个数组进行排序。类似于冒泡排序。

step1：先根据数组，创建一个最大堆；
step2：将根节点元素与数组最后一个元素进行交换，此时已经固定最大值的位置，类似于冒泡排序；
step3：将数组长度减1，且此时根节点的左右孩子节点均满足堆特性，加入交换后的根节点需要进行调整，使整棵树满足堆特性（此时step2中获得的最大值，不参与堆的构成）；
step4：循环处理step2和step3，直到数组元素为1。

二、代码实现

堆的创建buildHeap以及父节点调整heapify函数实现，请参考分治算法四：二叉堆的创建

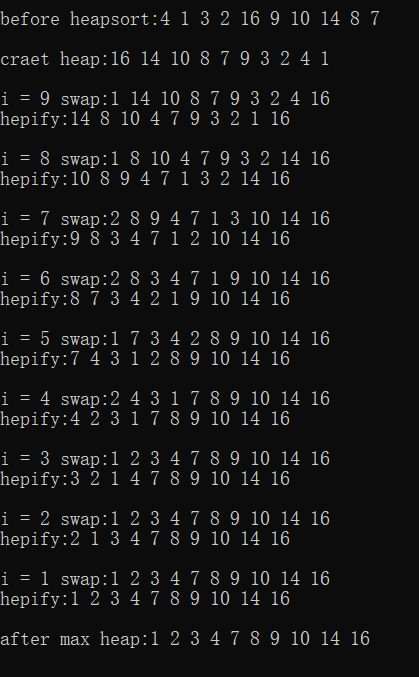
void heapSort(void *a, int size, int heapSize, int(*comp)(void *, void *))
{
    int heapSizeTemp = heapSize;
    // 根据原始数组创建堆
    buildHeap(a, size, heapSize, intGreater);
    printfList("\ncraet heap:", (int*)a, heapSize);

    for (int i = heapSize - 1; i > 0; i--)
    {
        printf("\ni = %d ", i);
        // 将堆顶元素与数组最后一个元素交换，确定此轮的最值
        swap(a + i * size, a, size);
        printfList("swap:", (int*)a, heapSize);
        // 因为此轮的最值已经确定，将堆的规模递减，并进行调整，获取剩余元素中的最值（根节点）
        heapSizeTemp--;
        // 堆顶元素与数组末端元素交换后，对当前堆进行调整
        heapify(a, size, 0, heapSizeTemp, intGreater);
        printfList("hepify:", (int*)a, heapSize);
    }
}

int main(void)
{
    int heap[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
    int heapSize = sizeof(heap) / sizeof(heap[0]);

    printfList("\nbefore heapsort:", heap, heapSize);
    heapSort(heap, sizeof(int), heapSize, intGreater);
    printfList("\nafter max heap:", heap, heapSize);

    while (1);
    return 0;
}

三、测试结果