分治算法四：二叉堆的创建
一、二叉堆概念
1、二叉堆的数据结构，可以由一个数据对象来表示，实际上是一个完全二叉树，即除最后一层外，其他层的结点数均达到最大值，且最后一层的填充为从左到右进行。
2、数组与二叉堆的表示如下：
将数组a[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}表示成二叉堆如下：
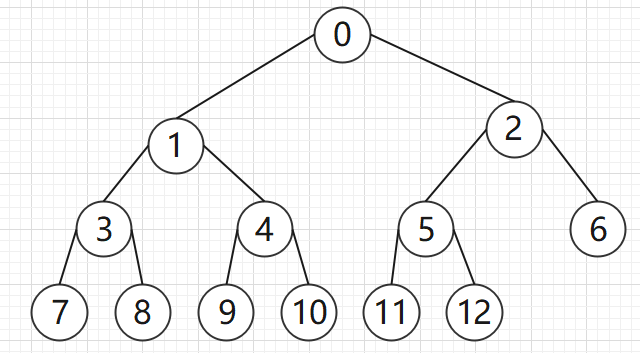
3、父节点、左叶子节点、右叶子节点
假设树的根节点为array[0]，对于给定节点的小标为i，则：
父节点索引为： （i - 1） / 2
左叶子节点索引为： 2 * i + 1
右叶子节点索引为： 2 * i + 2
3、最大堆、最小堆（或大顶堆、小顶堆）
最大堆：父节点的值不小于子节点的值，即array[i / 2] >= array[i]
最小堆：父节点的值不大于子节点的值，即array[i / 2] <= array[i]
二、性质维护（以最大堆为例）
1、背景：假设在数组A中，元素A[i]为完全二叉树的左、右两个孩子都已构成堆，但A[i]与两个孩子间不符合堆的性质，需要将其调整，使之满足堆的性质。
2、问题描述：数组A[1...n]预期存储一个完全二叉树，其中以A[i]为父节点的左、右子树已经构成最大堆，进行调节后，使A[i]为根节点的二叉树满足最大堆的性质。
3、问题思路：
第一步，将A[i]与左右节点进行比较，无非两种情况：与左叶子节点交换，或者与右叶子节点交换；
第二步，交换后，被交换的叶子节点可能不满足堆的性质，需要继续进行调节；
第三步[问题分解]，以被交换的叶子节点为根节点，继续判断调整，将原问题转化成小规模的问题（减少了二叉树的一层）；
第四步，使用递归处理
三、堆的创建
根据给出的数据，创建最大堆或最小堆，创建过程以及测试代码如下：
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 数组打印
static void printfList(char *info, int *array, int len)
{
printf("%s", info);
for(int i = 0; i < len; i++) {
printf("%d ", array[i]);
}
printf("\n");
return;
}
// 交换两个变量的值
void swap(void *x, void *y, int size)
{
void *temp = (void*)malloc(size);
memcpy(temp, x, size);
memcpy(x, y, size);
memcpy(y, temp,size);
free(temp);
}
// 在左右子树满足堆特性的前提下（最简单情形为左右子树为单个元素），判断父节点加入后，是否满足堆特性并进行调整
void heapify(void *a, int size, int parent, int heapSize, int(*comp)(void *, void *))
{
// 根据父节点索引i，得到左叶子节点和右叶子节点的索引，根节点的索引从0开始
int left = 2 * parent + 1;
int right = 2 * parent + 2;
int most;
// 比较左叶子节点和父节点大小，most = max(left, parent)
if (left < heapSize && comp(a + left * size, a + parent * size) > 0) {
most = left;
} else {
most = parent;
}
// 比较右叶子节点和most节点, most = max(right, most)
if (right < heapSize && comp(a + right * size, a + most * size) > 0) {
most = right;
}
// 此时most = max(parent, left, right); 若不满足堆特性，将most与父节点进行交换，并对交换后的叶子节点继续判断
if (most != parent) {
swap(a + parent * size, a + most * size, size);
heapify(a, size, most, heapSize, comp);
}
}
// 因为最后一层无叶子节点，故从倒数第二层开始，从底向上依次判断；当判断某个父节点时，可以保证左右子树均满足堆特性
void buildHeap(void *a, int size, int length, int(*comp)(void *, void *))
{
for (int i = (length / 2) - 1; i >= 0; i--) {
// 单次判断过程，直到根节点为止，使整棵树满足堆特性
heapify(a, size, i, length, comp);
printf("i = %d ", i);
printfList("buildHeap:", (int *)a, length);
}
}
// 比较函数
int intGreater(void *x, void *y)
{
return *(int *)x - *(int *)y;
}
int intLess(void *x, void *y)
{
return *(int *)y - *(int *)x;
}
int main(void)
{
int heap[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
int heapSize = sizeof(heap) / sizeof(heap[0]);
printfList("\nbefore max heap:", heap, heapSize);
buildHeap(heap, sizeof(int), 10, intGreater);
printfList("after max heap:", heap, heapSize);
printfList("\nbefore min heap:", heap, heapSize);
buildHeap(heap, sizeof(int), 10, intLess);
printfList("after min heap:", heap, heapSize);
while (1);
return 0;
}
四、测试结果
原始数组形成的二叉树为:
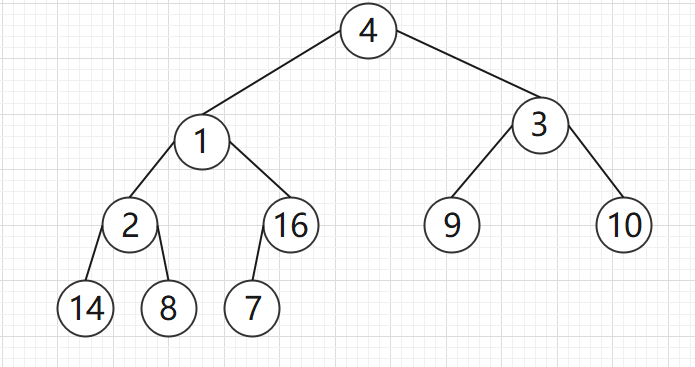
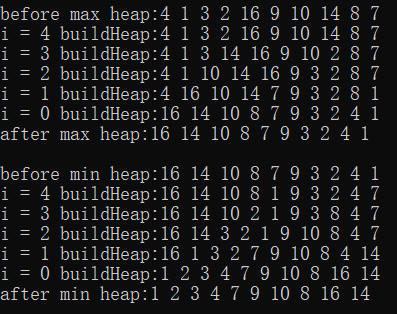
堆的调整过程以及最后结果如下图所示：
