分治算法一:汉诺塔
一、分治算法与递归
(1)分治算法,是指将一个规模较大的问题分解成多个小规模的子问题进行处理;当问题规模足够小时,处理策略就相当简单明了了;
(2)若这些子问题有相似的处理方法,则可以使用递归结构处理;
(3)递归-三步走:
递归出口:通常是问题规模最小时,最简处理策略;
递归过程:将大规模问题,逐步拆解成小问题的过程,递归的精髓皆在于此;
本层递归处理:各问题处理过程的衔接,还未理解透彻,处理比较麻烦。
(4)分治策略:
分解:将问题分解成若干个子问题;
治理:递归解决各子问题;
合并:将子问题的解合并成原问题的一个解。
二、汉诺塔问题
(1)问题说明:有三根柱子A、B、C,A柱上有n个大小不同的圆盘,大盘在下,小盘在上;需要将A柱上的盘子移动到C柱上,同样保持大盘在下小盘在上,移动过程中不允许大盘叠放在小盘上。
(2)分析:当仅A柱上仅有一个圆盘时,直接将其放到C柱上即可——最小规模问题,递归出口;
若A上有n(n>1)个圆盘,则将其前n-1个圆盘移动到过渡柱B上,然后将其转化成最小规模问题处理——分解策略,递归过程;
(3)因为盘子最后都要放到一个柱子上,且大盘在下小盘在上(默认没有相同大小的盘子),所以各个盘子都是唯一的
三、代码实现
// 查找x柱子上最底下一个圆盘的下标(当前x柱子上仅剩下一个圆盘,所以在current数组中有唯一下标)
int pickTopDisk(char *current, char x)
{
int i = 0;
while (current[i] != x) {
i++;
}
return i;
}
/*
* Description:三根木柱,将一根木柱上的圆盘借助中间木柱移动到另外一根木柱上,大圆盘不能放在小圆盘上
* input: 各圆盘的位置数组current,圆盘数量num,圆柱位置标识A、B、C
* current的下标可以理解为各盘子的标记,下标越大盘子越大
* current的内容表示当前该盘子放置的位置,A-源柱子,B-过渡柱子,C-目标柱子
* output: 动态输出圆盘移动步骤
*/
static int hanoiTower(char *current, int num, char A, char B, char C)
{
// count表示移动次数
static int count = 0;
int i = 0;
// 递归出口:当只有一个盘子时,直接将其移动到目标盘
// 仅有一个盘子时,此时盘子应在A柱子上(单个递归过程),需要明确该盘子的大小,即在current中的下标,将该下标对应内容改成C柱即可
if (num == 1) {
// 当前current中,仅有一个A,获取其下标
i = pickTopDisk(current, A);
// 模拟从A柱移动到C柱的操作,并增加操作次数
current[i] = C;
count++;
printf("move %d disk %d: %c -> %c \n", count, i + 1, A, C);
return 0;
}
// 递归过程:当当前需要移动的盘子不只一个时,需要先将A柱的n-1个盘子移动到B盘(此时,A依旧是源柱,B成为目标柱,C为过渡柱)
hanoiTower(current, num - 1, A, C, B);
// 本层递归处理:通过上一步骤的处理后,A柱上只剩下最大一个盘,下标为n-1,将其移动到C上
current[num - 1] = C;
count++;
printf("move %d disk %d: %c -> %c \n", count, num, A, C);
// 此时,B上有很多A之前的盘子,A空了,C上有一个A之前最大的盘子
// 下面将B作为源柱,A作为过渡,C依旧为目标柱,且需要移动的盘子数量减一(因为已经将最大的盘子移动到C柱了)
hanoiTower(current, num - 1, B, A, C);
return 0;
}
四、测试结果
测试代码:
#include <stdio.h>
#define DISK_NUM 4
// hanoiTower()函数实现
int main(void)
{
char current[DISK_NUM] = {'A', 'A', 'A', 'A'};
char A = 'A';
char B = 'B';
char C = 'C';
hanoiTower(current, DISK_NUM, A, B, C);
while (1);
return 0;
}
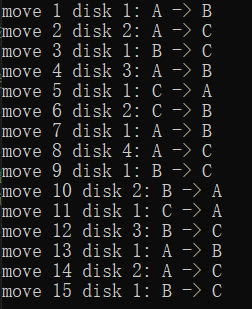
测试结果: