LCT浅(糙)谈
1.引出问题
动态树问题,要支持加/删边,和查询/修改操作。
如果树边没有改变,可以用树链剖分解决。
怎么转到动态树呢?实链剖分,实儿子没有什么实际含义,灵活可变。
我们可以用Splay维护这些实链。
2.辅助树
1.每一个Splay维护一个实链的信息。
2.原树与辅助树的节点对应。
3.在LCT中每棵Splay的根节点的父亲节点指向原树中这条链的父亲节点。
4.认父不认子,很重要的性质,保证辅助树分为多颗Splay。父亲找不到虚儿子。
5.只用考虑辅助树,原树没用。
3.具体操作
下面抄自OI Wiki(代码质量不好)和FlashHu的博客(WC讲课老师推荐)
为保证时间复杂度,要在改变辅助树后Splay。
函数顺序大致参考WC讲课老师金靖的PPT(害怕侵权,不作上传)。
I.Splay原有操作
1.splay
与一般Splay不同,这里要判断x的父亲是否为根。还要更新下传根到点的所有懒标记。(见update操作)
void splay(int x)
{
update(x);
for(int y;y=fa[x],!isroot(x);rotate(x))
{
if(!isroot(y))
{
rotate(get(x)==get(y)?y:x);
}
}
pushup(x);
}2.rotate
也要判父亲是否为根。
void splay(int x)
{
update(x);
for(int y;y=fa[x],!isroot(x);rotate(x))
{
if(!isroot(y))
{
rotate(get(x)==get(y)?y:x);
}
}
pushup(x);
}II.LCT特有操作
1.Access(x)
x到原树根变成实链,某些边受影响可能变虚边。
(所有操作的基础,LCT的关键)
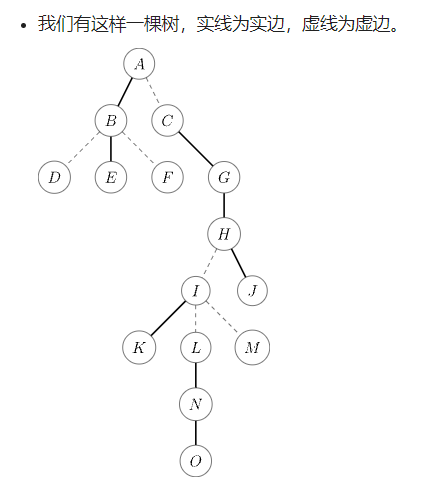
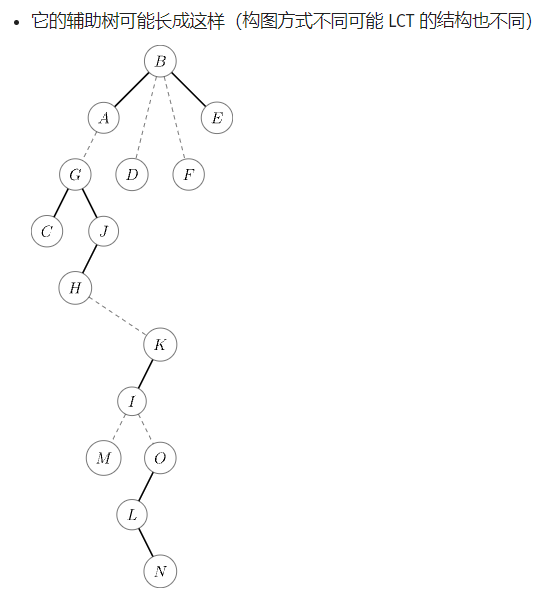
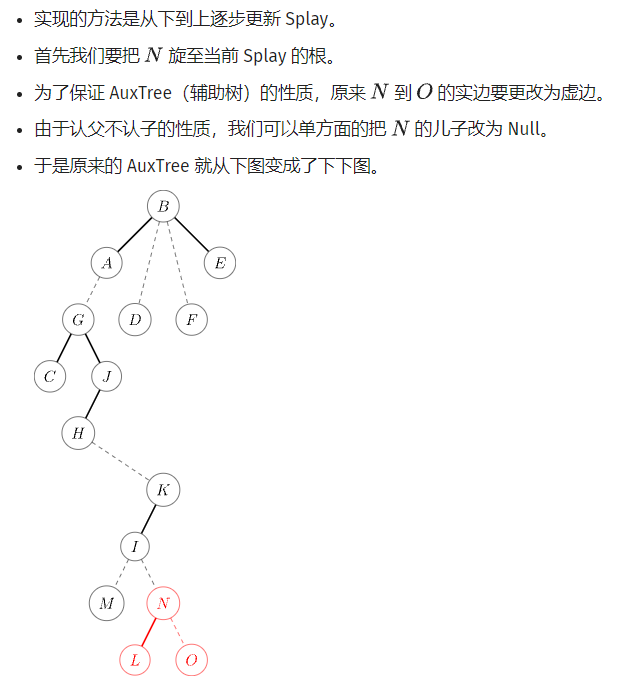
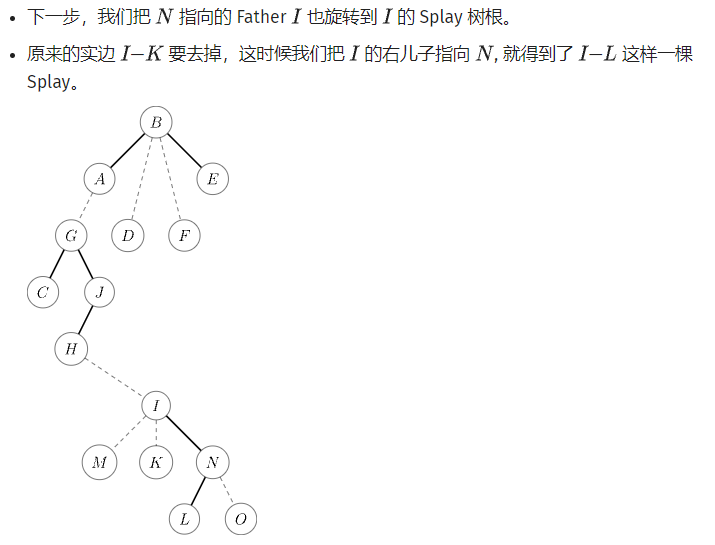
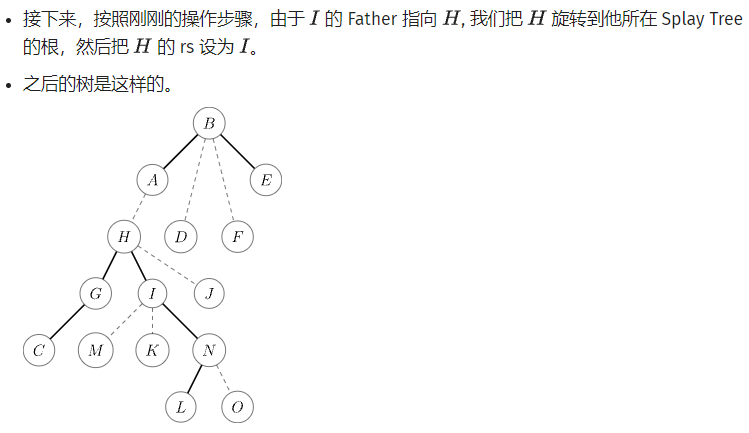

统共4步:
将当前节点转到根上,Splay基操;之前节点变成右儿子(路径放到实链上);更新;转到父亲,继续第1步。
这样,和父亲的边就在实链上了。同时,由于一直放在右儿子,x最终会变成Splay中最右的点。
void access(int x)
{
int y;
for(y=0;x;x=fa[y=x])
{
splay(x),ch[x][1]=y,pushup(x);
}
}2.makeroot
将x变为原树的根
通过access让x和原树的根在同一颗Splay中,子孙都要左右翻转(打懒标记)。
HQX解释:x在access后成为Splay最右的点(中序遍历最后),翻转整个Splay(每层都要翻转),x成为成了最左的点(深度最小)。
由于放到根上比较特殊,也很好做,所以这个函数可以大大地帮助我们实现其他操作。
void makeroot(int x)
{
access(x);
splay(x);
rev(x);
}3.findroot
找x所在原树的根。
把x与树根放在同一条链,维护Splay,找最左的点(根),记得下传标记。(同上HQX所述)
int findroot(int x)
{
access(x);
splay(x);
while(ch[x][0]){
pushdown(x);
x=ch[x][0];
}
splay(x);
return x;
}4.split
将x到y的路径整出来
把x变为原树的根,让y与原树根(x)在同一条链,y变为Splay的根,所在Splay包含x到y路径。
void split(int x,int y)
{
makeroot(x);
access(y);
splay(y);
}5.link
把x和y连边
把x变为原树的根,利用根无父亲的特点,让y成为x的父亲,完成连边。
记得在makeroot后,判断x和y是否在同一颗原树内,防止非法连边破坏树的结构。
void link(int x,int y)
{
makeroot(x);
int z=findroot(y);
if(z!=x)fa[x]=y;
}6.cut
把x和y连的边删掉
把x变为原树的根,y只能为x的右儿子(根深度最浅,没有左儿子即更浅的点),直接断开。
记得在makeroot后,判断x和y是否在同一颗原树内,防止断不存在的边。
void cut(int x,int y)
{
makeroot(x);
int z=findroot(y);
if(z==x&&fa[y]==x&&!ch[y][0])
{
fa[y]=ch[x][1]=0;
pushup(x);
}
} 7.reverse
void rev(int x)
{
swap(ch[x][0],ch[x][1]);
tag[x]^=1;
}翻转操作
左右儿子翻转,给当前点更改懒标记。
8.update
更新下传根到点的所有懒标记
顺序绝对不能搞反,通过递归实现父亲先pushdown。
void update(int x)
{
if(!isroot(x))update(fa[x]);
pushdown(x);
}III.具体操作
1.删/加边:cut/link(x,y)
2.x到y路径异或和:split(x,y),答案在y上。
3.修改x的权值:splay(x),x变为Splay根节点,再修改x,避免对其他点造成影响。
#include<bits/stdc++.h>
#define mid ((l+r)>>1)
#define inf 1000000007
using namespace std;
int n,m,a[1000005];
long long read()
{
long long x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+ch-48,ch=getchar();
return x*f;
}
struct LCT
{
int next[1000005],to[1000005],h[1000005],cnt;
int fa[1000005],ch[1000005][2],sz[1000005],tag[1000005];
int s[1000005],v[1000005];
void pushup(int x)
{
sz[x]=sz[ch[x][0]]+sz[ch[x][1]];
s[x]=s[ch[x][0]]^s[ch[x][1]]^v[x];
}
void rev(int x)
{
swap(ch[x][0],ch[x][1]);
tag[x]^=1;
}
void pushdown(int x)
{
if(!tag[x])return;
if(ch[x][0])rev(ch[x][0]);
if(ch[x][1])rev(ch[x][1]);
tag[x]=0;
}
bool isroot(int x)
{
return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;
}
int get(int x){return x==ch[fa[x]][1];}
void rotate(int x)
{
int y=fa[x],z=fa[y],k=get(x),kk=get(y);
if(!isroot(y))ch[z][kk]=x;
ch[y][k]=ch[x][k^1];
fa[ch[x][k^1]]=y;
ch[x][k^1]=y;
fa[y]=x;fa[x]=z;
pushup(y);pushup(x);
}
void update(int x)
{
if(!isroot(x))update(fa[x]);
pushdown(x);
}
void splay(int x)
{
update(x);
for(int y;y=fa[x],!isroot(x);rotate(x))
{
if(!isroot(y))
{
rotate(get(x)==get(y)?y:x);
}
}
pushup(x);
}
void access(int x)
{
int y;
for(y=0;x;x=fa[y=x])
{
splay(x),ch[x][1]=y,pushup(x);
}
//return y;
}
void makeroot(int x)
{
access(x);
splay(x);
rev(x);
}
int findroot(int x)
{
access(x);
splay(x);
while(ch[x][0]){
pushdown(x);
x=ch[x][0];
}
splay(x);
return x;
}
void split(int x,int y)
{
makeroot(x);
access(y);
splay(y);
}
void link(int x,int y)
{
makeroot(x);
int z=findroot(y);
if(z!=x)fa[x]=y;
}
void cut(int x,int y)
{
makeroot(x);
int z=findroot(y);
if(z==x&&fa[y]==x&&!ch[y][0])
{
fa[y]=ch[x][1]=0;
pushup(x);
}
}
}t;
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
n=read(),m=read();
for(int i=1;i<=n;i++)
{
t.v[i]=read();
}
for(int i=1,opt,x,y;i<=m;i++)
{
opt=read(),x=read(),y=read();
if(opt==0)
{
t.split(x,y);
printf("%d\n",t.s[y]);
}
if(opt==1)
{
t.link(x,y);
}
if(opt==2)
{
t.cut(x,y);
}
if(opt==3)
{
t.splay(x);
t.v[x]=y;
t.pushup(x);
}
}
return 0;
}
4.写在最后
以前总觉得LCT是难以企及的高峰,是洪水猛兽。
但现在仔细钻研,回头再看,并没有那么难。
模板题只有2k+bytes,思路也很明了。
(但是非模板题都很难)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号