PRIM+KRUSKAL

第一次修改2020/8/14：1.增加了Kruskal；2.对一些不准确、不详细的地方进行了改动；3.别问我为什么Kruskal用链式前向星，而Prim用邻接矩阵（因为能用Prim你的空间也不会炸）

最小生成树的定义

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边

简单来说，就是权值和最小的树

Prim的思路

设图的顶点集合为U，树的顶点集合为V

从图中任意一点出发，找到N-1条边(x,y)，x∈U，y∈V，且权值最小。

通俗的讲，就是不断找权值最小且不产生闭环的N-1条边

例子

废话不多说，先上图

如下图所示

 

 

 

 

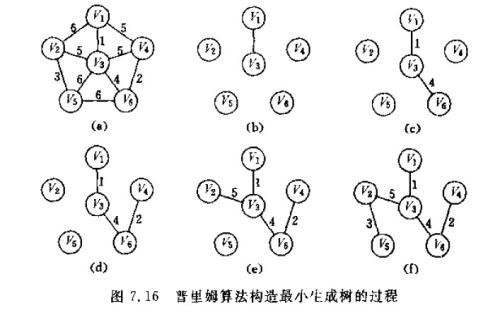
（1）从V3出发

（2）找到边(V3,V1)，符合条件且最小，将V1加入V

以此类推……

（N）找到边(V2,V5)，符合条件且最小，将V5加入V，最小生成树构造完成

 代码（C++）

代码又长又臭，bug一堆，欢迎巨佬吐槽

务必记住，要将A的初值赋为正无穷

for (int i=2;i<=n;i++)
    {
        lowcost[i]=a[i][1];//将与V1(或任意一点)有关的边存入lowcost（与各点最小权值）
    }
    for (int i=1;i<n;i++)
    {
        minval=1000000;//初始化最小值为正无穷
        for (int j=1;j<=n;j++)
        {
                if (lowcost[j]>0&&lowcost[j]<minval)//如果当前权值不为0(即未连接过)且更小
                {
                    k=j;//记录当前点
                    minval=lowcost[j];//将最小值存入
                }
        }
        ans+=minval;//统计最小生成树最小权值和
        lowcost[k]=0;//标记该点
        for (int j=1;j<=n;j++)
        {
                if (lowcost[j]>0&&lowcost[j]>a[k][j])//由于U集合点增加，需更新与各点最小权值边
                {
                    lowcost[j]=a[k][j];
                }
        }
    } 

输入

7 9
1 2 28
1 6 10
2 3 16
2 7 14
3 4 12
4 5 22
4 7 18
5 6 25
5 7 24

输出

99

算法对比

Prim和Kruskal都是最小生成树算法

Prim:O(N^2)

Kruskal:O(M log M)

很明显，边数最多为O(N-1)N/2 

（直接理解为N^2）

我们可以感性理解,由于log很小

所以在绝大部分情况下kruskal是优于prim的

而Prim很容易被卡

能用Kruskal还是尽量用吧（我就被亲身卡过（QAQ算法歧视））

Kruskal

将所有边按照权值排序 

用并查集来操作

 

bool cmp(node a,node b){return a.dis<b.dis;}
int find(int x)
{
    if(fa[x]==x)return fa[x];
    else return fa[x]=find(fa[x]);
}
void kruskal()
{
    lowcost=0;tot=0;
    for(int i=1;i<=m;i++)fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        int x=e[i].from,y=e[i].to;
        int xx=find(x),yy=find(y);
        if(xx!=yy)
        {
            lowcost+=e[i].dis;
            fa[xx]=yy;
            tot++;
        }
        if(tot==n-1)break;
    }
    printf("%lld\n",lowcost);
}