关于扩展中国剩余定理（excrt）的证明与拙见

问题
解同余方程（有解）
\(x \equiv a1(mod \ p1)\)
\(x \equiv a2(mod \ p2)\)
\(……\)
\(x \equiv an(mod \ pn)\)
相较于一般的中国剩余定理，这题没有\(ai⊥mi\)的限制
所以要用扩展中国剩余定理（\(excrt\)）
推柿子（没有易证，可能错误很多）
考虑不断将两个方程合并
把
\(x \equiv a1(mod \ p1)\)
\(x \equiv a2(mod \ p2)\)
变成\(x=a1+p1k1=a2+p2k2\)
再变成\(p1k1-p2k2=a2-a1\)
套个exgcd(https://oi-wiki.org/math/gcd/)
求解\(p1k1-p2k2=(p1,p2)\)，两边（即k1）\(\times \frac{a2-a1}{(p1,p2)}\)搞出上面的解（因为有解，所以\((p1,p2)|(a2-a1)\)）
然后求出当前方程组的解\(x0=a1+p1k1\),\(p3=[p1,p2]\)，\(a3=x0 \ mod \ p3\)，
合并成\(x0 \equiv a3(mod \ p3)\)
(为什么\(m\)是这样,https://www.cnblogs.com/HYDcn666/p/114514ber.html)
拙见
1.乘法会爆，建议用乘法黑科技（在下面）
2.我认为尽量用\(excrt\)，毕竟没有互质的限制（其实是我不太会一般的\(crt\)）
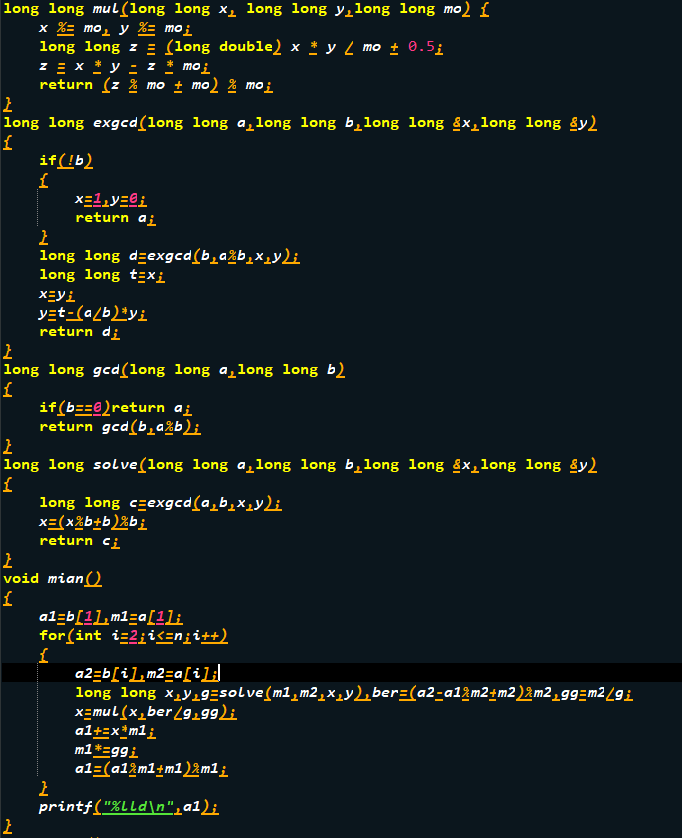
核心代码