20202325 实验九《数据结构与面向对象程序设计》实验报告
# 20202325 2021-2022-1 《数据结构与面向对象程序设计》实验九报告
课程:《程序设计与数据结构》
班级: 2023
姓名: 和宇
学号:20202325
实验教师:王志强
实验日期:2021年12月18日
必修/选修: 必修
## 1.实验内容
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
## 2. 实验过程及结果
(1)初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)
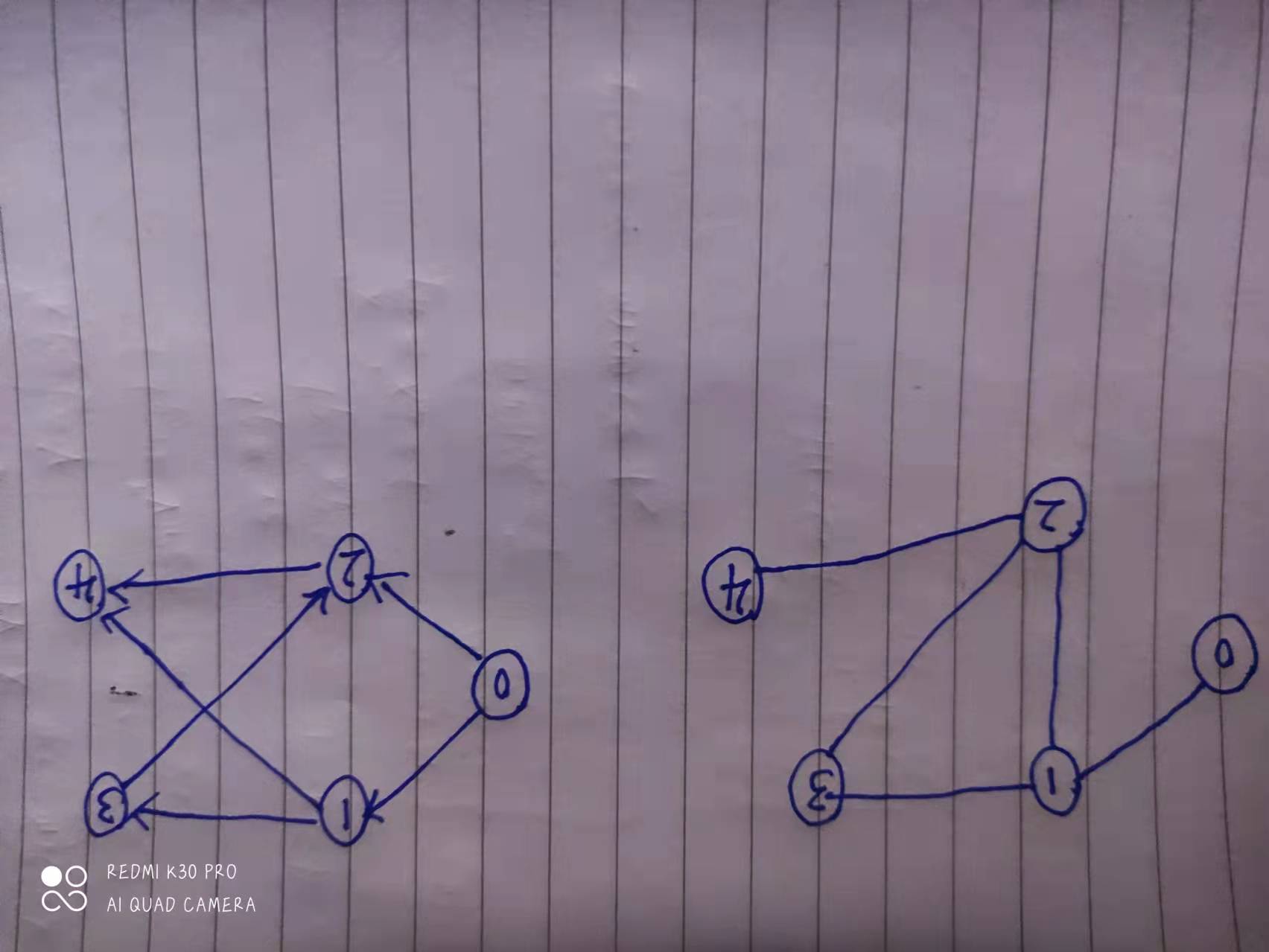
无向图:
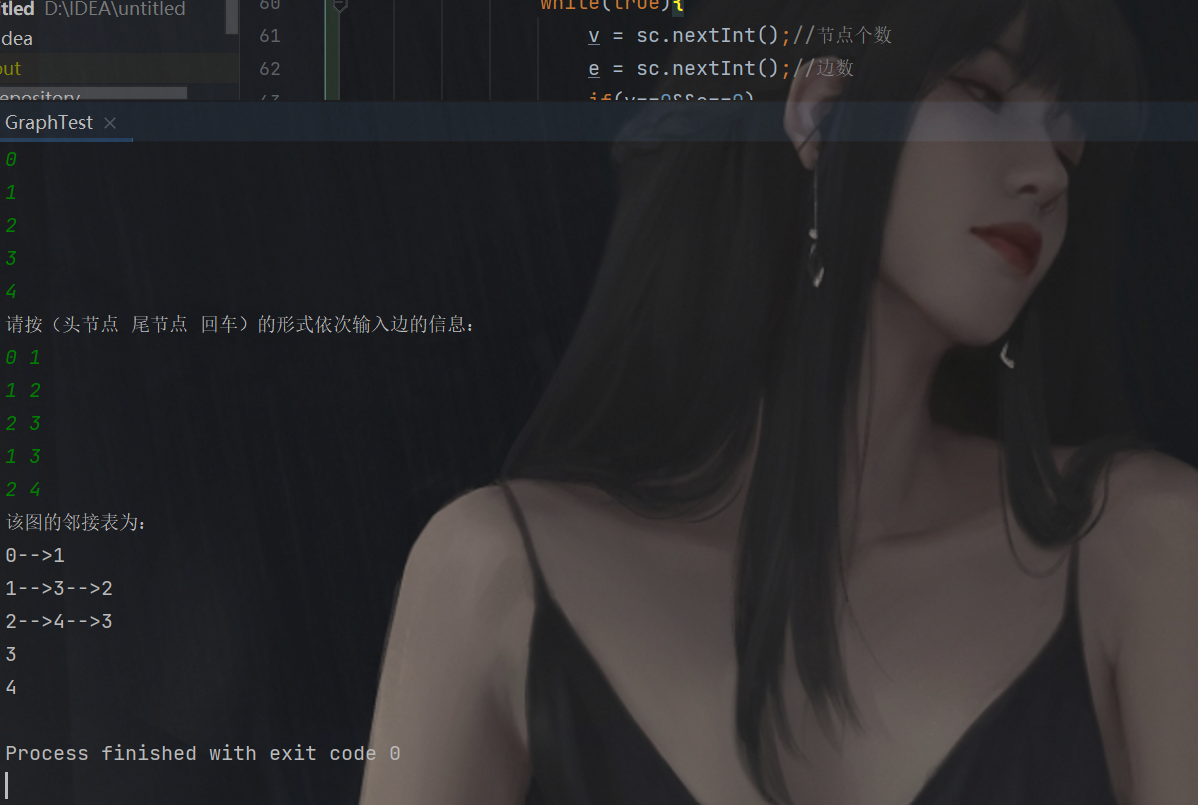
有向图:

代码:
import java.util.Scanner; //图的构造 public class Graph { int VertexNum;//节点个数 int EdgeNum;// 边的条数 Vertex[] verArray;//图的邻接表中存储节点的数组 //依次读取节点、边,完成图的构建 public Graph() { Scanner scan = new Scanner(System.in); System.out.println("构造有向图输入2,构造无向图输入1:"); int a = scan.nextInt(); System.out.println("输入节点个数和边的条数:"); VertexNum = scan.nextInt(); EdgeNum = scan.nextInt(); // String[] top =new String[VertexNum]; // String[] bottom = new String[VertexNum]; verArray = new Vertex[VertexNum]; System.out.println("请依次输入节点的名称:"); for (int i=0;i<VertexNum;i++){ Vertex vertexmem = new Vertex(); vertexmem.verName = scan.next(); vertexmem.edgeLink = null; verArray[i] = vertexmem; } System.out.println("请按(头节点 尾节点 回车)的形式依次输入边的信息:"); for (int i=0;i<EdgeNum;i++){ String preName = scan.next();//头节点 // top[i]=preName; String folName = scan.next();//尾节点 Vertex preV = getVertex(preName); // bottom[i] =folName; Vertex folV = getVertex(folName); if (preV == null || folV == null){ System.out.println("输入错误!输入了不存在的顶点!请重新输入:"); i--; continue; } Edge edge = new Edge(); edge.tailName = folName; //将边加入到节点的链表中去 edge.broEdge = preV.edgeLink;//循环 preV.edgeLink = edge;//放在出始地的后面 if(a==2){ Edge edgeelse = new Edge(); edgeelse.tailName = preName; edgeelse.broEdge = folV.edgeLink; folV.edgeLink = edgeelse; } } //获取入度和出度 if(a==2){ Scanner sc = new Scanner(System.in); int v,e; int in,out; System.out.println("输入节点个数和边数:"); while(true){ v = sc.nextInt();//节点个数 e = sc.nextInt();//边数 if(v==0&&e==0) break; Graph1 g = new Graph1(v,e); System.out.println("输入头和尾:"); for(int i1=0;i1<e;i1++){ in = sc.nextInt(); out = sc.nextInt(); g.insertEdge(in,out); } System.out.println("出度:"); for(int i1=0;i1<v;i1++){ if(i1!=0) System.out.print(" "); System.out.print(g.outDegree(i1)); } System.out.print("\n"); System.out.println("入度:"); for(int i1=0;i1<v;i1++){ if(i1!=0) System.out.print(" "); System.out.print(g.inDegree(i1)); } System.out.print("\n"); } } } //根据节点名称获取该节点 public Vertex getVertex(String verName){ for (int i=0;i<VertexNum;i++){ if (verArray[i].verName.equals(verName)) return verArray[i]; } return null; } class Graph1{ private int vertex; private int edge; private int graph[][]; Graph1(int v,int e){ vertex = v; edge = e; graph = new int[v][v]; for(int i=0;i<v;i++){ for(int j=0;j<v;j++){ graph[i][j]=0; } } } void insertEdge(int in,int out){ graph[in][out] = 1; } int outDegree(int theVertex){ int cnt=0; for(int i=0;i<vertex;i++){ cnt += graph[theVertex][i]; } return cnt; } int inDegree(int theVertex){ int cnt=0; for(int i=0;i<vertex;i++){ cnt += graph[i][theVertex]; } return cnt; } } }
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)
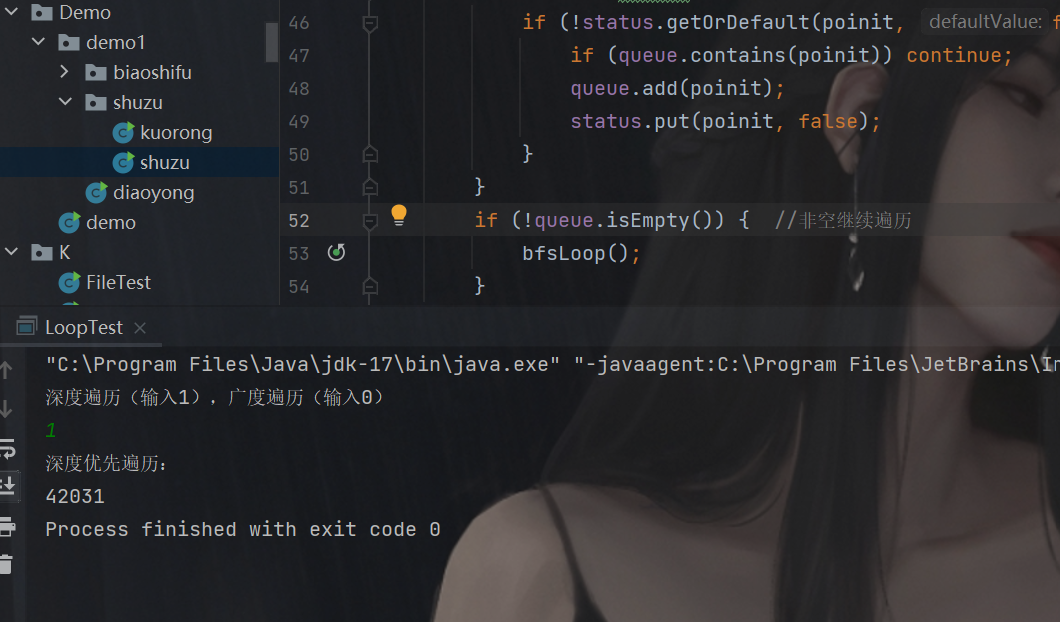
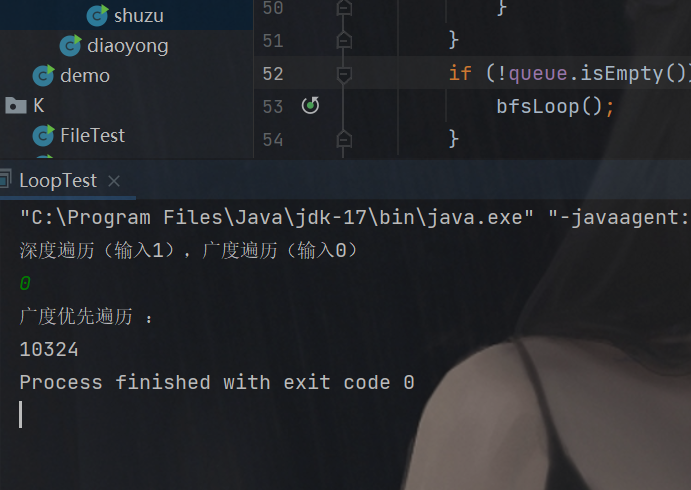
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环
拓扑序列:
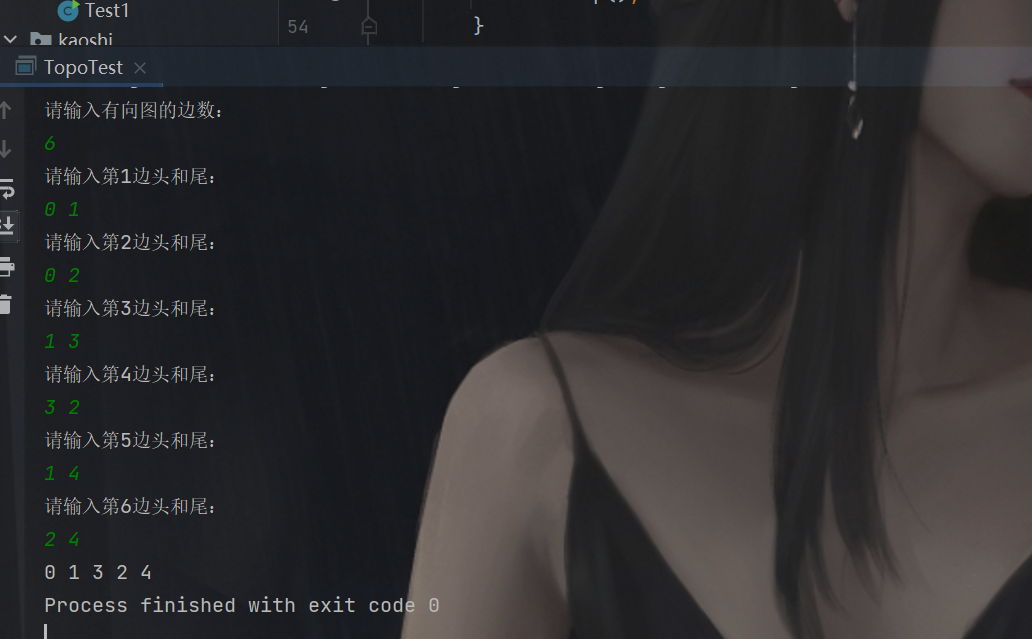
存在环:
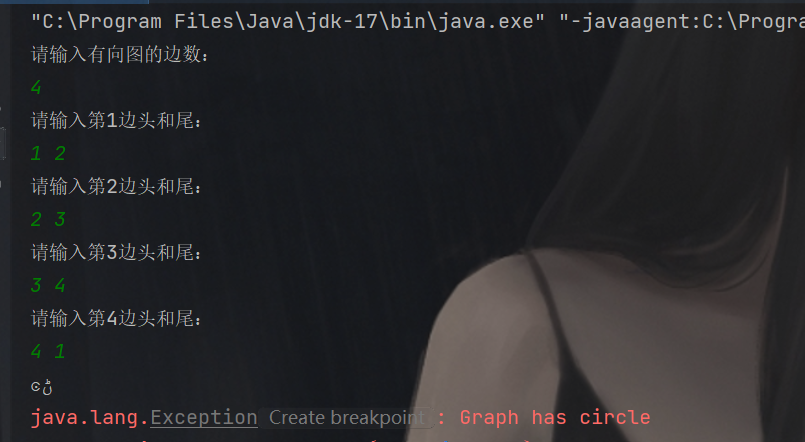
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出
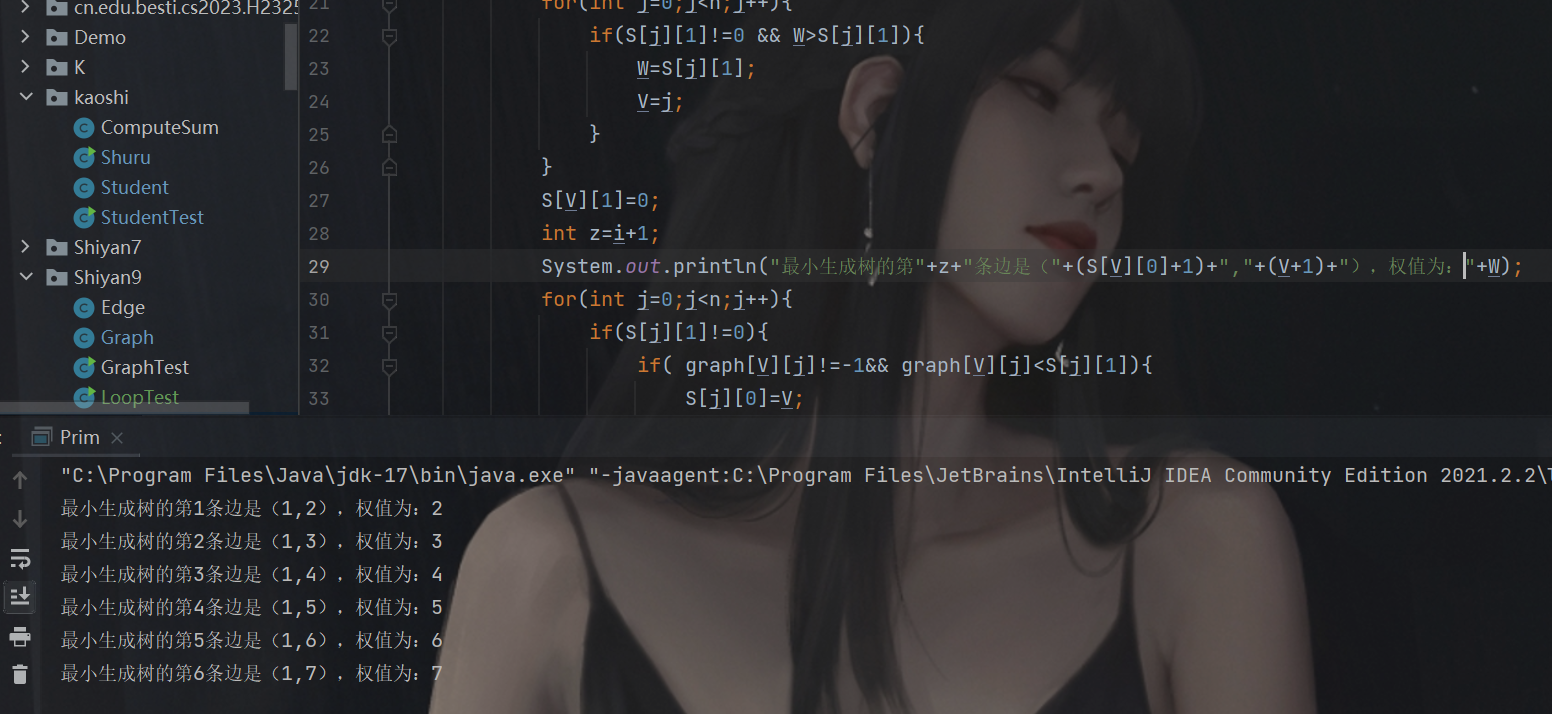
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)
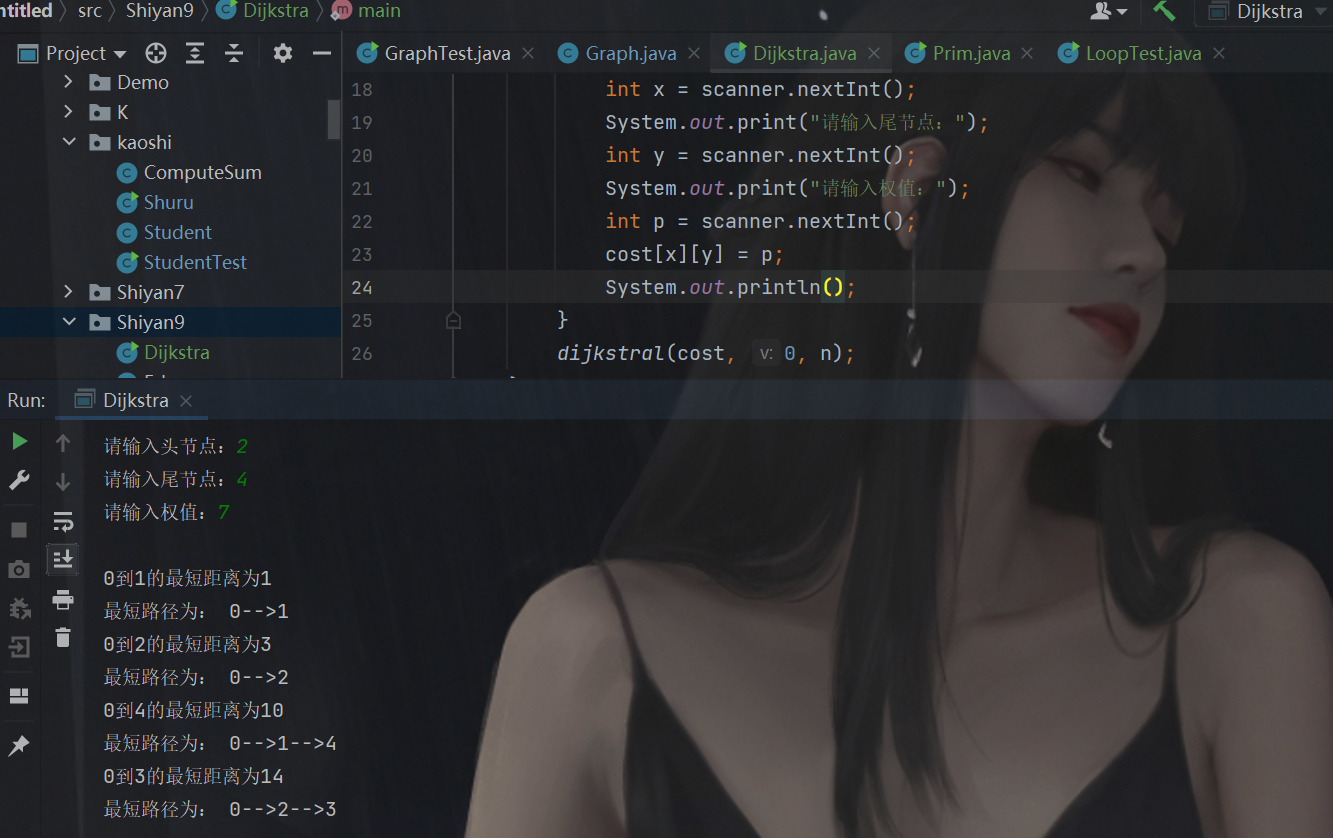
代码:
import java.util.Arrays; import java.util.Scanner; public class Dijkstra { public static void main(String args[]){ Scanner scanner = new Scanner(System.in); System.out.println("请输入节点个数和边数:"); int n = scanner.nextInt(); int m = scanner.nextInt(); int[][] cost = new int[n][n]; for(int i = 0; i<n; i++){ Arrays.fill(cost[i], Integer.MAX_VALUE); } for(int i = 0; i<m; i++){ System.out.print("请输入头节点:"); int x = scanner.nextInt(); System.out.print("请输入尾节点:"); int y = scanner.nextInt(); System.out.print("请输入权值:"); int p = scanner.nextInt(); cost[x][y] = p; System.out.println(); } dijkstral(cost, 0, n); } public static void dijkstral(int[][] cost, int v, int n){ int[] dist = new int[n]; //用于保存v到其他点的最短距离 int[] s = new int[n]; //用于保存已计算过的顶点 int[] rear = new int[n]; //rear[i]保存v到顶点i的最短路径顶点数 int[][] q = new int[n][n]; //q[v][i]保存v到i的最短路径 //初始化s和rear for(int i = 1; i<n; i++){ s[i] = 0; rear[i] = -1; } //初始化dist和q for(int i = 1; i<n; i++){ dist[i] = cost[v][i]; if(dist[i] < Integer.MAX_VALUE){ q[i][++rear[i]] = v; q[i][++rear[i]] = i; } } s[v] = 1; int j, min, m; for(int i = 0; i<n-1; i++){ min = Integer.MAX_VALUE; m = v; //寻找和v距离最近的点 for(j = 1; j<n; j++){ if(dist[j] < min && s[j] == 0){ min = dist[j]; m = j; } } if(m != j){ s[m] = 1; System.out.println(v + "到" + m + "的最短距离为" + dist[m]); System.out.print("最短路径为: "); for(int k = 0; k<=rear[m]; k++){ if(k == rear[m]) { System.out.print(q[m][k]); break; } System.out.print(q[m][k] + "-->"); } System.out.println(); //更新dist,就是上面所说的从v2出发 for(int k = 1; k<n; k++){ if(dist[k] > (cost[m][k] + dist[m]) && s[k] == 0 && cost[m][k] != Integer.MAX_VALUE){ dist[k] = cost[m][k] + dist[m]; for(int k1 = 0; k1<=rear[m]; k1++){ //更新路径 q[k][k1] = q[m][k1]; } rear[k] = rear[m]; q[k][++rear[k]] = k; } } } } } }
#问题和感悟
随着学习的深入,遇到的问题和困难也越来越多,有时候一个小小的错误就需要改n个小时。这是倒数第二次实验,我觉得对java语言编程越来越得心应手,但这些问题对我仍然是一个超级大工程,所以需要我付出更多的时间来学习和巩固java的学习成果。
## 参考资料
- [《Java程序设计与数据结构教程(第4版)》]



