20202325 实验八 《结构基础与面向对象程序设计》实验报告
# 20202325 2021-2022-1 《数据结构与面向对象程序设计》实验八报告
课程:《程序设计与数据结构》
班级: 2023
姓名: 和宇
学号:20202325
实验教师:王志强
实验日期:2021年11月25日
必修/选修: 必修
## 1.实验内容
1.参考教材PP16.1,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
2.基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
3.自己设计并实现一颗决策树
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
4.输入中缀表达式,使用树将中缀表达式转换为后缀表达式,并输出后缀表达式和计算结果(如果没有用树,正常评分。如果用到了树,即使有小的问题,也酌情给满分)
提交测试代码运行截图,要全屏,包含自己的学号信息
#过程
1.参考教材PP16.1,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
代码:
Node:
package BinaryTree; public class Node { int data; //节点数据 Node leftChild; //左子节点的引用 Node rightChild; //右子节点的引用 boolean isDelete;//表示节点是否被删除 public Node(int data){ this.data = data; } //打印节点内容 // public void display(){ // System.out.println(data); // } @Override public String toString() { return "data=" + data +","+ "leftChild=" + leftChild + ","+" rightChild=" + rightChild + ","+"isDelete=" + isDelete; } }
BinareTree:
package BinaryTree; public class BinaryTree1 implements Tree { private Node root; //插入节点 public boolean insert(int data) { Node newNode = new Node(data); if(root == null){//当前树为空树,没有任何节点 root = newNode; return true; }else{ Node current = root; Node parentNode = null; while(current != null){ parentNode = current; if(current.data > data){//当前值比插入值大,搜索左子节点 current = current.leftChild; if(current == null){//左子节点为空,直接将新值插入到该节点 parentNode.leftChild = newNode; return true; } }else{ current = current.rightChild; if(current == null){//右子节点为空,直接将新值插入到该节点 parentNode.rightChild = newNode; return true; } } } } return false; } //查找节点 public Node find(int key) { Node current = root; while(current != null){ if(current.data > key){//当前值比查找值大,搜索左子树 current = current.leftChild; }else if(current.data < key){//当前值比查找值小,搜索右子树 current = current.rightChild; }else{ return current; } } return null;//遍历完整个树没找到,返回null } //中序遍历 public void infixOrder(Node current){ if(current != null){ infixOrder(current.leftChild); System.out.print(current.data+" "); infixOrder(current.rightChild); } } //前序遍历 public void preOrder(Node current){ if(current != null){ System.out.print(current.data+" "); preOrder(current.leftChild); preOrder(current.rightChild); } } //后序遍历 public void postOrder(Node current){ if(current != null){ postOrder(current.leftChild); postOrder(current.rightChild); System.out.print(current.data+" "); } } //找到最大值 public Node findMax(){ Node current = root; Node maxNode = current; while(current != null){ maxNode = current; current = current.rightChild; } return maxNode; } //找到最小值 public Node findMin(){ Node current = root; Node minNode = current; while(current != null){ minNode = current; current = current.leftChild; } return minNode; } public static void main(String[] args) { BinaryTree1 tree = new BinaryTree1(); tree.insert(21); tree.insert(50); tree.insert(20); tree.insert(11); tree.insert(27); tree.insert(23); tree.insert(25); tree.insert(100); System.out.println(tree.findMax().data); System.out.println(tree.findMin().data); System.out.println(tree.find(100)); System.out.println(tree.find(10)); System.out.println("中序:"); tree.infixOrder(tree.root);//中序 System.out.println(); System.out.println("后序:"); tree.postOrder(tree.root);//后序 System.out.println(); System.out.println("先序:"); tree.preOrder(tree.root);//前序 } }
运行结果:

2.基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
结果:
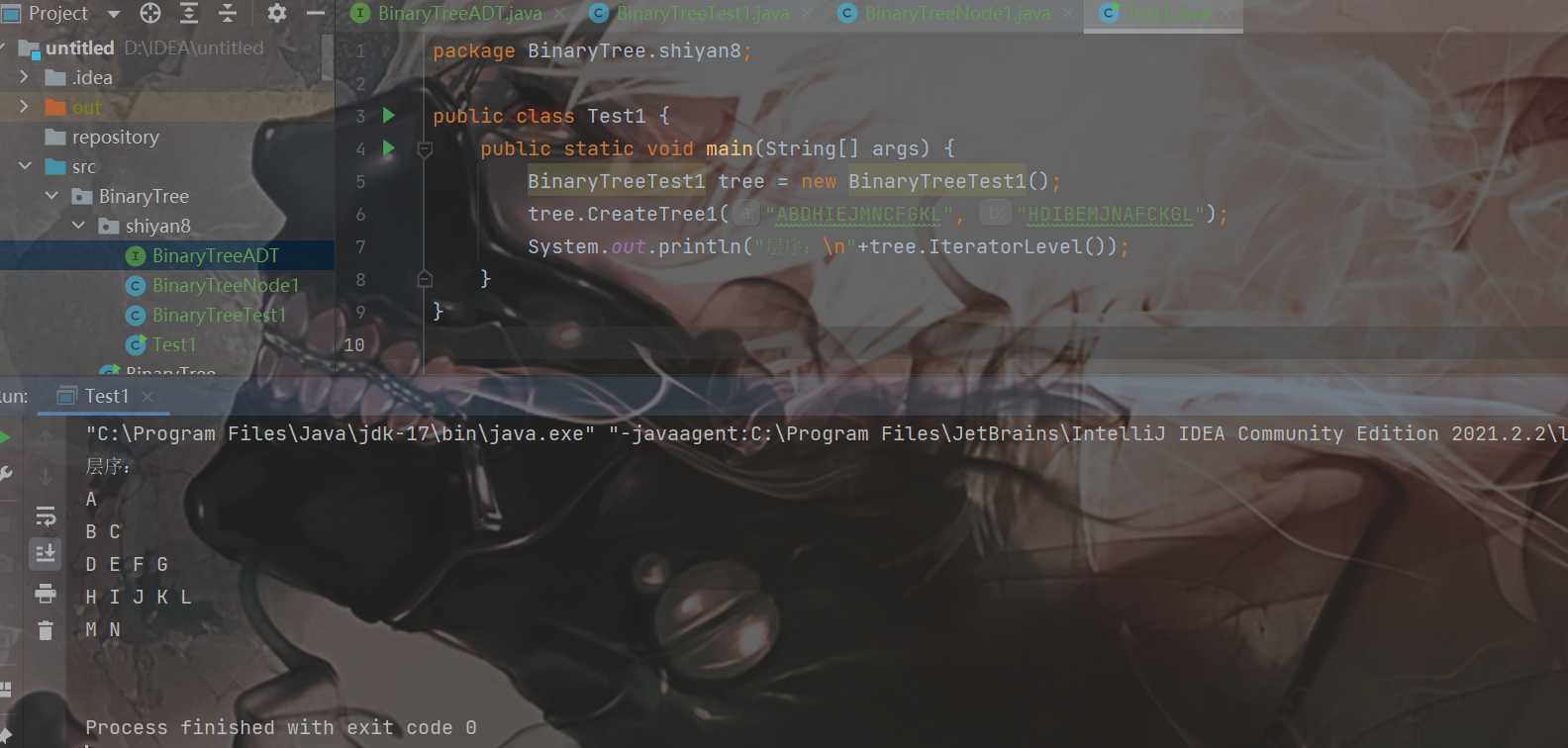
3.自己设计并实现一颗决策树
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台



4.输入中缀表达式,使用树将中缀表达式转换为后缀表达式,并输出后缀表达式和计算结果(如果没有用树,正常评分。如果用到了树,即使有小的问题,也酌情给满分)
提交测试代码运行截图,要全屏,包含自己的学号信息


#问题
1.编程没有思路,不知道该怎么入手。
解:翻教材,问同学,上网查资料;
2.程序与程序之间互相联系,互相继承和引用,改了一个程序,结果前面的许多貌似不相关的程序直接报错,回过头来找却发现已经找不到是哪里出问题了,东拼西凑处处报错。
#感悟
感悟还是老生常谈,编写程序时迷迷糊糊的,感觉脑子已经不够用了……得潜心学习一段时间了。
## 参考资料
- [《Java和Andriod开发学习指南(第二版)人民邮电出版社》]
- [《Java软件结构与数据结构(第三版)清华大学出版社》]



