回溯算法之n皇后问题

今天在看深度优先算法的时候，联想到DFS本质不就是一个递归回溯算法问题，只不过它是应用在图论上的。OK，写下这篇博文也是为了回顾一下回溯算法设计吧。

学习回溯算法问题，最为经典的问题我想应该就是八皇后问题了。

一、适用范围

　　回溯算法应用的范围当然是很多了，那么归纳一下：如果一个问题中，没有很好的数学模型来解决，或者有数学模型解决，但是很难实现，那么我们就可以使用回溯算法来求解。

二、定义

回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。

用回溯算法解决问题的一般步骤：
1 针对所给问题，定义问题的解空间，它至少包含问题的一个（最优）解。
2 确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
3 以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。
问题的解空间通常是在搜索问题解的过程中动态产生的，这是回溯算法的一个重要特性。

 

例题：八皇后问题

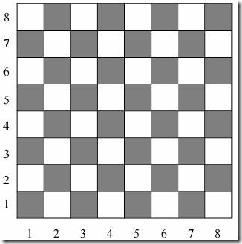
在8*8国际象棋棋盘上，要求在每一行放置一个皇后，且能做到在竖方向，斜方向都没有冲突。国际象棋的棋盘如下图所示：

显然，每一行可以而且必须放一个皇后，所以n皇后问题的解可以用一个n元向量X=（x1,x2,.....xn）表示，其中，1≤ i≤ n且1≤ xi≤ n，即第n个皇后放在第i行第xi列上。

由于两个皇后不能放在同一列上，所以，解向量X必须满足的约束条件为:xi≠ xj;

若两个皇后的摆放位置分别是（i,xi）和（j,xj），在棋盘上斜率为-1的斜线上,满足条件i-j=xi-xj;在棋盘上斜率为1的斜线上，满足条件i+j=xi+xj;

综合两种情况，由于两个皇后不能位于同一斜线上，所以，解向量X必须满足的约束条件为:
|i-xi|≠ |j-xj|

 

#include <cmath>
#include <cstdlib>
#include <iostream>
using namespace std;
const int MAXSIZE=100;

int Pos_Queen[MAXSIZE];//Pos_Queen[k]代表的含义是第k行的皇后应放在第Pos_Queen[k]列处
int count=0;//全局变量，用来记录所有可能性数量
bool Is_Safe(int k)//考察皇后k放置在Pos_Queen[k]列是否安全
{
    for(int i=1; i<k; i++)
        if( Pos_Queen[k] == Pos_Queen[i] || abs(k-i) == abs(Pos_Queen[k]-Pos_Queen[i]) )
            return false;
    return true;
}

//打印皇后摆放情况
void Print_Queen( int queenList[], int n )
{
    cout<<"Case "<<(++count)<<":"<<endl;
    cout<<"  ";
    for( int i=1; i<=n; i++ )
    {
        cout<<i<<" ";
    }
    cout<<endl;
    for( int i=1; i<=n; i++ )
    {
        cout<<i<<" ";
        for( int j=1; j<queenList[i]; j++ )
        {
            cout<<"* ";
        }
        cout<<"Q ";
        for( int j=1; j<( n - queenList[i]+1 ); j++ )
        {
            cout<<"* ";
        }
        cout<<endl;
    }
    cout<<endl;
}

void queue(int n)
{
    int i,k;
    for(i=1; i<=n; i++)
        Pos_Queen[i]=0;
    k=1;
    while( k>=1 )
    {
        Pos_Queen[k] = Pos_Queen[k]+1;   //在下一列放置第k个皇后
        while( Pos_Queen[k] <= n && !Is_Safe(k) )
            Pos_Queen[k] = Pos_Queen[k]+1;//搜索下一列
        if( Pos_Queen[k] <= n && k == n )//得到一个输出
        {
            count++;
            //Print_Queen(Pos_Queen,n);
            //return;//若return则只求出其中一种解，若不return则可以继续回溯，求出全部的可能的解
        }
        else if( Pos_Queen[k] <= n && k < n )
            k = k+1;//放置下一个皇后
        else
        {
            Pos_Queen[k]=0;//重置Pos_Queen[k],回溯
            k = k-1;
        }
    }
}

int main()
{
    int n;
    cout<<"输入皇后个数n:";
    cin>>n;
    queue(n);
    cout<<n<<"皇后问题共有"<<count<<"种放法"<<endl;
    return 0;
}

 

 

学习心得：

1.在编写递归枚举程序之前，需要深入分析问题，对模型精雕细琢。一般还应对解答树的结点数有一个粗略的估计，作为评价模型的重要依据。

2.如果在回溯法中试用了辅助的全局变量，则一定要及时把它们恢复原状。例如，若函数有多个出口，则需要在每个出口处恢复被修改的值。

3.从解答树的角度讲，回溯法正是按照深度优先的顺序在遍历解答树。