二维凸多边形相交判定 （converx polygon intersection detection） Dobkin & Kirkapatrick 1983

学堂在线上邓俊辉老师提到的converx polygon intersection detection方法，课上没有讲得很详细，现在找出这篇论文详细介绍该方法。

论文链接：[PDF] Fast Detection of Polyhedral Intersection | Semantic Scholar

 预处理方法

在多边形边界的最高和最低y坐标处进行切割，将多边形边界分解为两个单调的多边形边链，按照y坐标递增的方向确定这两条链的角和边的顺序。由于是凸多边形，这样的两条链的方向一定是左向或者右向（图中的P_R和P_L，注意不是在左边的为R在右边的为L，而是左向的为L，右向的为R），在每条链的头和尾分别加上一条水平的无穷射线（如果是P_R则是指向x轴正无穷，如果是P_L则指向负无穷），这样每条链就组成了monotone polygonal sectors (MPS). 单调多边形扇区。

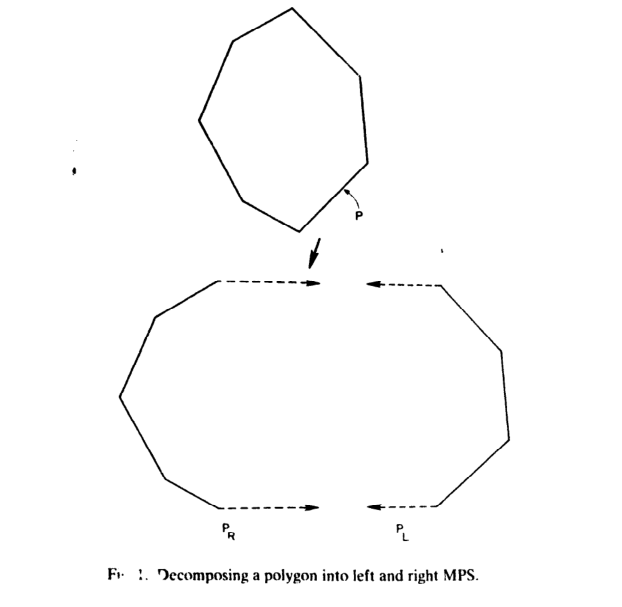
 上述这个划分两条链的操作可以在O(logn)时间内完成，且MPS具有的性质是P = P_L ∩ P_R and P ⊆ P_L, P_R。

二维相交判断

引理1 :  凸多边形P和Q相交当且仅当 P_L 和 Q_R相交且 P_R和Q_L相交。

构造出两个MPS后，剩下的问题就是利用二分搜索找出链相交的边。在每次二分迭代中，选择每个链的一条边（一般是最中间的边mid edge）所在的直线构成支撑线。利用两条支撑线的交点提供的信息(基于MPS的属性)允许我们每次迭代都可以忽略一个(或两个)多边形的一半的边，而且不会错过交点的检测。原始的边不会被删除，只是原始的结构信息会被丢弃，并且每次迭代会构造新的水平射线边缘来保持MPS的属性。下面通过一个简单的例子来说明，迭代后新组成的链相交当且仅当原来的链相交。

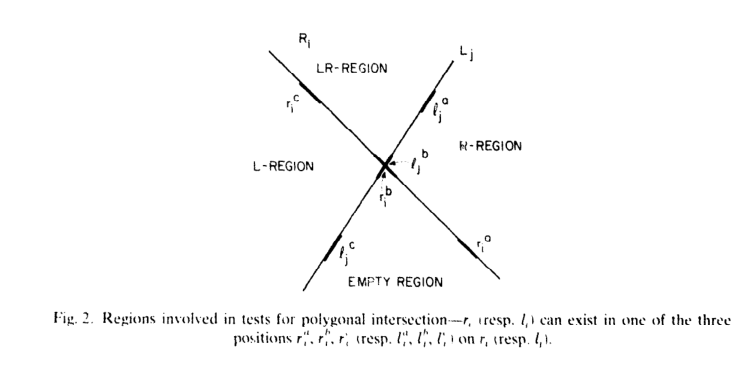
如Fig.2所示，设R是一个凸多边形的指向右向的链，包含边（r₁,r₂,...,r_m），L是另一个凸多边形的指向左向的链，包含边（l₁,l₂,...,l_n），其中r₁和r_m，l₁和l_n都是水平射线，其余的边都是有限长度的边。Fig.2给出了r_i这条边位于R_i这条直线上的三种情况（lj这条边同理）。

每次迭代都会选取i=[m/2]和j=[n/2]的边r_i和l_j进行考虑。设R_i和L_j是r_i和l_j所构成直线，那么这两条相交直线可以把空间分成R、LR、L和EMPTY四个区域（如果直线平行则是退化情况，因为凸性质R和L都会被限制在直线的一个半平面内，只需考虑R和L所在的两个半平面是否有交集即可）。其中R和L只能占据这四个区域中的其中两个区域（由于凸性质，R只会在r_i这条边的右边区域（LR和R），L只会在l_j这条边的左边区域（LR和L）），而此次迭代裁剪掉一半的边后，剩下的R和L存在于其中的某个区域。新的MPS（R'，R''和L'，L''）怎么保留由下面引理决定，其中R''是穿过r_i端点的水平射线的R的上半部分，R'是下半部分。（L'和L''同理）。

 翻译一下就是说，在LR区域位于EMPTY区域上方的情况下，（当然反过来也是一样的）

（1）如果r_i和l_j直接相交，那么直接判定原凸多边形P和Q相交，这是再好不过的情况。

（2）如果r_i的上端点不在LR区域内（l_j位置随意），（即r_i处在Fig.2中r_i^a）的位置，那么可以舍弃掉R链的下半部分R'，R和L相交当前仅当上半部分R''与L相交。如下图所示，由于凸性质，r_i以下的点都会被限制在R_i和r_i水平线相交的右下区域，不管怎么延伸，都不会穿过EMPTY REGION到L所在的区域，不可能再和L发生相交，因此可以直接舍弃R'部分的检测。

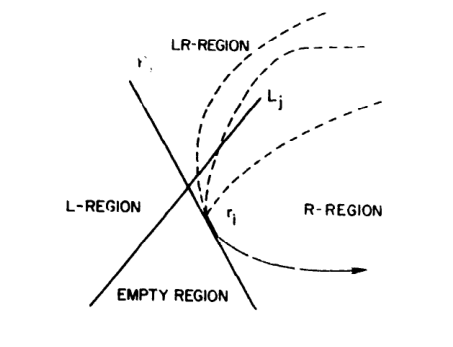
同理，如果l_j的上端点不在LR区域内（r_i位置随意），（即l_j处在Fig.2中l_j^c）的位置，那么可以舍弃掉L链的下半部分L'，R和L相交当前仅当上半部分L''与R相交。

 

 

（3）如果ri和lj的两端都位于LR区域，如果r_i的lower端点比l_j的lower端点低（高），则L和R相交当且仅当上半部分R''和L相交（L''和R相交）。从下图可以看出，r_i和l_j二者中最低的那部分链可以被去除而不影响相交检测的结果，因为这部分链是递减的，不可能和上半部分相交。

 

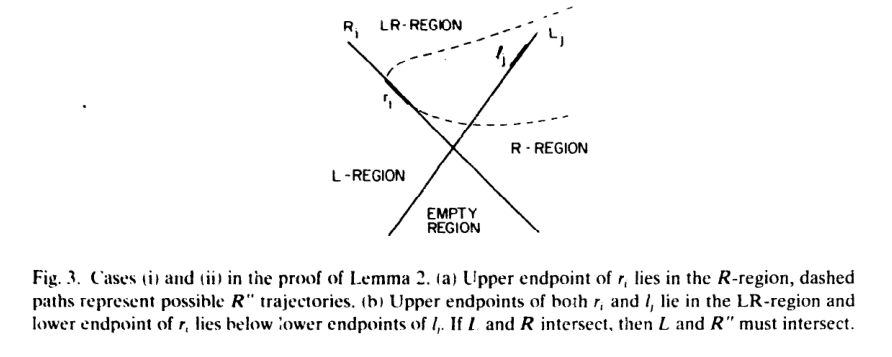
 总结就是说，如Fig.2所示，r_i和l_j的位置总共有3*3=9种情况，无论是哪一种情况，都可以归结到引理2的三种情况中，如果有其中一条边的端点不在LR区域，则可以舍弃与EMPTY区域相邻的那一半的链；如果两条边的端点都在LR区域，则可以舍弃两条链中离LR区域最远的那一半的链。

总之根据ri和lj与直线交点的位置情况，可以舍弃一半的链，从而让问题在O(log(n))复杂度内可以解决。正如邓俊辉老师课堂的PPT所示：

 

 

 

 

 

 

 

 

 

 

 

 

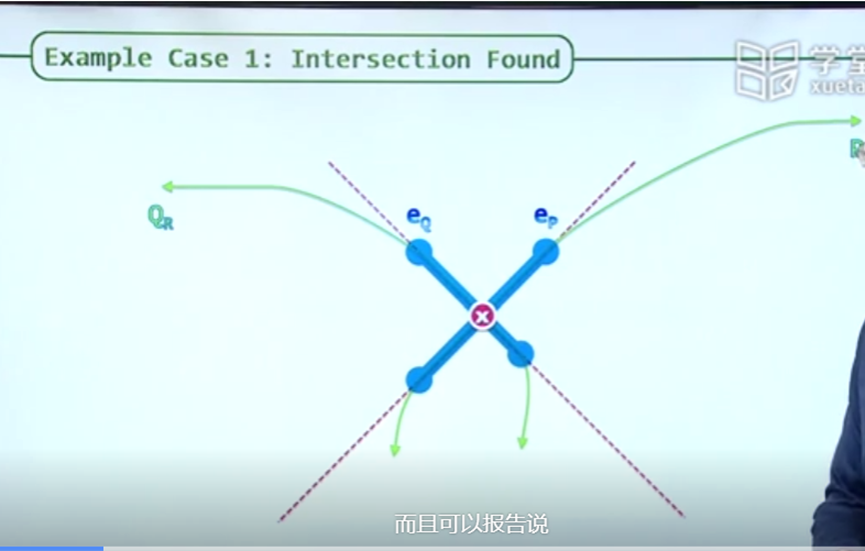
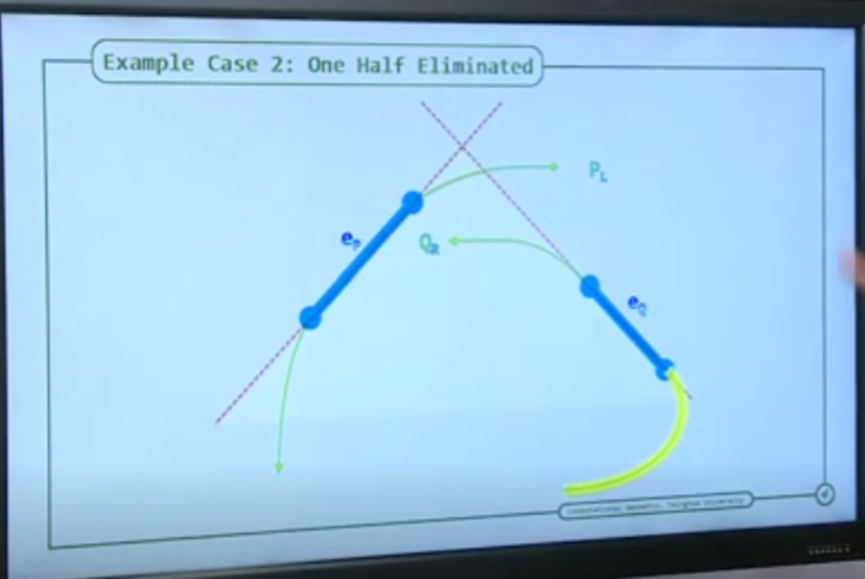
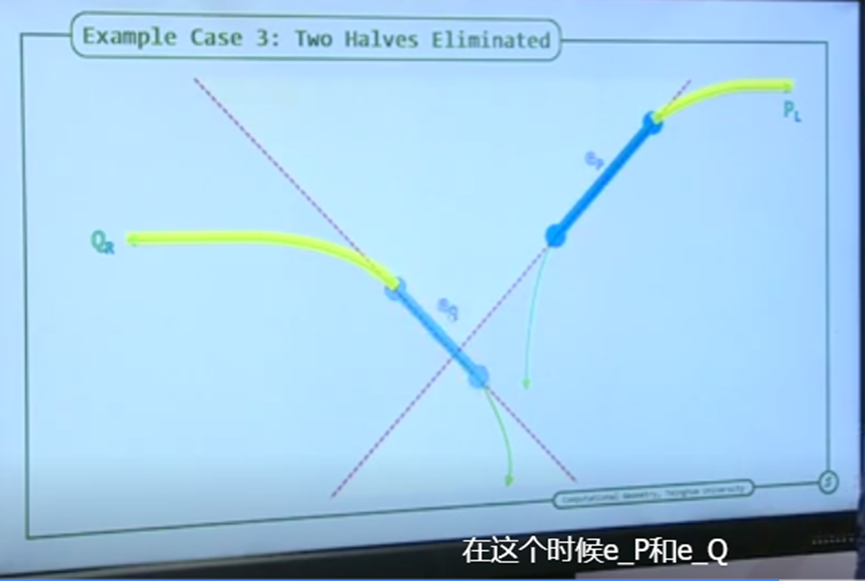
该论文还提到了三维凸包的相交检测算法，时间关系以后再更新。