【题解】 2月19日 厦门双十中学NOIP2014模拟D2 T1 采药人的切题规则
Made by 退役的OIer
第一次写博客,写得不好 or 不清楚的可以 在下方留言,我会尽量改进的!
好啦~~~回到正题,题面见传送门
【问题描述】
【输入格式】
【输出格式】
【输入输出样例】
【数据规模】
solution:
首先我们可以看出这就是Joseph问题(如果不会请移步至Joseph问题)
最最基础的算法就是模拟啦~~~
数p道题就切掉当前这个,重复k次,我们当然可以使用循环链表模拟这个过程(很形象的)
部分代码如下:

void pre() { FOR(i,1,n) { l[i]=(i==1)?n:i-1; r[i]=(i==n)?1:i+1; } return; } void del(int x)//在链表中删除x(即把x两边的连起来) { r[l[x]]=r[x]; l[r[x]]=l[x]; return; } //在main中 int pos=n; while(k-->0) { FOR(i,1,p) pos=r[pos]; del(pos); } printf("%d",pos);
哈哈,是不是很简单?
然而,仔细一想,整个算法时间复杂度为O(pk)
emmm....显然炸得裂开
我们急需寻找一个更为高效的算法
递推!
我们发现,一个队列进行一次切题操作后,长度会减小1,而队列开头到切掉的题的下一个
即可以从此处重新编号1~(n-1),相当于对当前队列编号整体减p
(自己推一推,模拟 切 一 道 题 的过程)
假设f[i][j]为队列长度为 i 时 , 切掉的第 j 道题的编号
则有以下递推式:
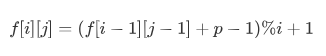
初态即
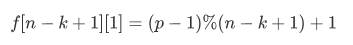
又可以发现,f数组没有必要,只用一个变量pos即可
那么代码就出来了:

//在main中 int pos=(p-1)%(n-k+1)+1; FOR(i,n-k+1,n) { pos=(pos+p-1)%i+1; } printf("%d",pos);
分析一波发现,算法时间复杂度降到了O(k)
wow~~~优(yiu)秀(xiu)
欣喜地看看数据范围, ?@#(*%&@#!
k<=n<=10^14
这说明我们需要更~~~~~~~~高效的算法!
???(仔细想想怎么优化,想完再往下看)
就一个小优化即可:乘法加速
用乘法加速加法运算(是不是很简单)
(不对呀,这里有取模,怎么加速???)
很容易发现,取模并不是每次都有改变,就是说取模把加法分成了若干小段,每个小段中pos是连加的
每次 i 增加 1 时, pos 增加 p(是不是很像追及问题?)
那么每段中, i 就会增加 tmp, 其中
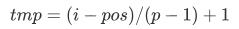
这样就很好办了~~~
再就不多说了,见完整代码

#include<cstdio> #define ll long long #define rll register ll ll n,p,k,len,pos; int T; int main() { scanf("%d",&T); while(T-->0) { scanf("%lld%lld%lld",&n,&p,&k); if(p==1) printf("%lld\n",k);//注意特判p==1的时候 else { len=n-k+1;pos=(p-1)%len+1; for(rll tmp(0);len+tmp<=n;tmp=(len-pos)/(p-1)+1) pos=(pos+tmp*p-1)%(len+=tmp)+1; printf("%lld\n",(pos+(n-len)*p-1)%n+1); } } return 0; }
是不是很简单?
复杂度也很简单,O(T * F(k) )(其中F(k)为关于k的函数,值很小,可近似为log(k))
愉快地 切 一 道 题 啦~~~
最后,
感谢 P.Y.Y 提供的官方题解平台~~~
感谢各位 巨佬&&神犇 的支持与鼓励~~~
可别忘了指正,转发与推荐哟~



