总之就是 | 初见 | 递推
修改记录:
2021.2.6
统一了题解题目格式
2021.2.3
在文末添加了大佬的递推回顾链接
啊那什么是递推呢?
即:从已知到未知。
利用观察发现前面已知数据从而得出递推公式,再利用递推公式求解。
啊那它和递归有肾么区别?
即:从未知到已知,再从已知到未知。
举个例子的话:(源自洛谷题单:递推与递归)

那么下面开始总结近日的练习
题单链接
T 1 3 1 2 昆 虫 繁 殖
题目原链接
这是一道一本通上的例题,但是我并没有看课本的解法
思 路
这个题上来就当头一棒
过x月产y对卵
可能这一下就蒙了,这玩意怎么找递推公式?
但是还是要把题看完的嘛。
后面就有稍微熟悉点的东西了,
每对卵要过两个月长成成虫,且卵长成成虫后的第一个月不产卵(过x个月产卵)
但是好像还不是很明显,再看样例,可以看出实际上是有一定的关系可寻的,
对于样例,每过1个月每对成虫生2对幼虫,每对幼虫两个月长成成虫,
那么:
当月的成虫=上上个月(两个月前)的幼虫+上个月的成虫
当月的幼虫=上个月(一个月前)的成虫*2
再由这个特殊推向一般,
即得:
当月的成虫=一个月前成虫+两个月前的幼虫
当月的幼虫=x月前的成虫*y
设c[i]是当月的成虫数量,u[i]是当月的幼虫数量,表示上式可得:
c[i]=c[i-1]+u[i-2]
u[i]=c[i-x]*y
搞完这些,就可以代码实现了。
剩下的都在代码注释里面了(
上 代 码
#include <iostream>
using namespace std;
int long long c[60],u[60];//c是成虫的数量,u是幼虫的数量
int main()
{
int x,y,z;
cin>>x>>y>>z;
for(int i=1;i<=x;i++)
{
c[i]=1;u[i]=0;//因为过x月才产一次,所以在1~x月都只有1对成虫
}
for(int i=x+1;i<=z+1;i++)
{
u[i]=y*c[i-x];//本月幼虫是x月之前的成虫生的,所以幼虫数量就是i-x月的成虫*y
c[i]=c[i-1]+u[i-2];//因为两个月幼虫长成成虫,所以本月成虫就是上月的成虫数量+上上月的幼虫数量
}
cout<<c[z+1];//过了z月,即输出第z+1月的成虫数量
return 0;
}
本题总结
对于我来说最一开始想那些用的时间很长,但是一点一点分析还是可以出来的
蒟蒻叹气
T 1 3 1 3 位 数 问 题
题目原链接
又是一道例题
思路
在第一遍做的时候,看完题目毫无思路......
因为出现了因为语文差而产生的死亡性阅读偏差:
题目第一句话
在所有的N位数中,有多少个数中有偶数个数字3?
正常的断句
在所有的N位数中,有多少个/数中/有偶数个/数字3?
但是我的断句:
在所有的N位数中,有多少/个数中有/偶数/个数/字3?
导致我光看题看了三分钟......
看完题了还是没思路,看解析也不会,于是去问学长,问明白了。
果然还是我太菜,人家三分钟连代码都敲完了
st(Q A Q) 学长 (Q A Q)rz
经过我理解之后,思路是这样的:
分析每一位奇数个三和偶数个三的个数然后推导这一位的这两个数值和上一位的这连个数值有肾么关系
设f[i]为到当前位,3的个数为偶数的情况总数,g[i]则是3的个数为奇数的情况总数
这里的位数是从小到大,即由个位到百位,千位......
递推公式要先有个已知,也就是要有个头,于是分析个位的情况
| 0个3 | 0,1,2,4,5,6,7,8,9 | 9个 |
|---|---|---|
| 1个3 | 3 | 1个 |
| 也就是f[i]=9,g[i]=1 |
有了这个再去推普遍的情况
假设之前的位都已经推好了,如果要有偶数个3的话
- 当前位的0,1,2,4,5,6,7,8,9都可以和上一位的每一种有偶数个3的情况结合,产生新的有偶数个3的数。
(因为前者都有0个3,后者必有偶数个3,加在一起还是必有偶数个3) - 当前位的3可以和上一位的每一种有奇数个3的情况结合,产生新的有偶数个3的数
(因为前者有奇数个3,后者必有奇数个3,加在一起必有偶数个3)
所以可以推得f[i]=f[i-1]*9+g[i-1]
同样的道理,如果要有奇数个3的话
- 当前位的0,1,2,4,5,6,7,8,9都可以和上一位的每一种有奇数个3的情况结合,产生新的有奇数个3的数。
(因为前者都有0个3,后者必有奇数个3,加在一起必有奇数个3) - 当前位的3可以和上一位的每一种有偶数个3的情况结合,产生新的有奇数个3的数
(因为前者有奇数个3,后者必有偶数个3,加在一起必有奇数个3)
所以可以推得g[i]=g[i-1]*9+f[i-1]
(小学奇偶性的连续运用)
这样就完了......
吗?
起初我和学长都是这样认为的,于是提交.......
10*WA......
于是好像还差了点什么,于是再分析......
原来最后一位(最高位)不能是0,淦......
那么就需要在刚才的分析的基础上,添加一个特判
即当到最后一位的时候,上式(们)变为:
f[i]=f[i-1]* 8 +g[i-1]
f[i]=f[i-1]* 8 +g[i-1]
那么接下来就可以实现10*AC了
上 代 码
#include <iostream>
#include <cstdio>
using namespace std;
int n,f[1001],g[1001];//f是有偶数个3的数的个数,g是有奇数个3的个数
int main()
{
cin>>n;
f[1]=9;//第一位(个位)有9个数中是0个数字3
g[1]=1;//第一位中只有3有奇数(1个)数字3
int x=9;//每位考虑0-9(除3)的情况
for(int i=2;i<=n;i++)
{
if(i==n)
x--;//当i到最后一位(最高位)的时候,因为最高位不能是0,所以这里的x变为8,即考虑1~9(除3)的情况
f[i]=f[i-1]*x+g[i-1];
g[i]=g[i-1]*x+f[i-1];
f[i]%=12345;//按照题目要求模12345
g[i]%=12345;
}
cout<<f[n];
}
下面这个是从网上找到的,大体意思一样,也放出来吧
#include<iostream>
#include<cstdio>
using namespace std;
const int mod = 12345;
int num[1010][2];
int main()
{
int n;
num[1][0] = 9; num[1][1] = 1;
scanf("%d", &n);
int x = 9;
for (int i = 2; i <= n; ++i)
{
if (i == n)
--x;
num[i][0] = (num[i - 1][0] * x + num[i - 1][1]) % mod;
num[i][1] = (num[i - 1][1] * x + num[i - 1][0]) % mod;
}
printf("%d\n", num[n][0]);
}
本题总结
要分类讨论,假设递推
T 1 3 1 4 过河卒 + T 1 1 9 1 流 感 传 染 + T 1 1 9 4 移 动 路 线
为什么把这几道题放一块呢?
很简单,解法类似(或者说我的解法类似),都是图形中的递推
过河卒 思路
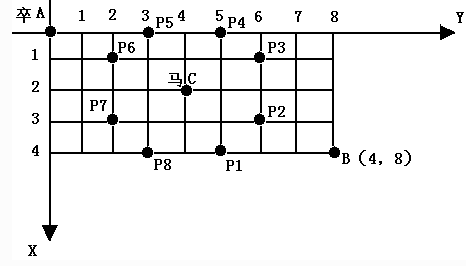
既然这个题给了图,那我就往图的方向去想
我们看它的问题:
从A点能够到达B点的路径的条数
于是我想到到达每个点的方案数,因为是有到达不了的点的,而最后要到达的点也是可以以此分析的。
假设A点的到达路径数为1,由题中说只能向下或向右,我们可以得出这样一个表
1 1 1 0 0 0 0 0 0
1 2 0 0 0 0 0 0 0
1 3 3 3 0 0 0 0 0
1 4 0 3 3 3 0 0 0
1 5 5 0 3 0 0 0 0
(可能比较难看懂,把马能到的点标为C,再把A和B加粗)
A 1 1 C 0 C 0 0 0
1 2 C 0 0 0 C 0 0
1 3 3 3 C 0 0 0 0
1 4 C 3 3 3 C 0 0
1 5 5 C 3 C 0 0 0
可以看出每个点都是它的上和左的和(因为只能向下、向右走卒)
那怎么解决最边上的呢?
这里的话我把A平移到的(1,1)其他的,也相应平移 [比如B变成(n+1,m+1)]
然后把最边上的一排和一列都初始化为0,这样的话对加法运算不会产生影响,也不会超越数组限制
还有一点就是如A,C这样的点,每次操作它们的时候得保证值不变(A始终为1,C始终为0)
主要就是用二维数组模拟坐标系来计算
过河卒 代码
#include <iostream>
using namespace std;
int long long sq[22][22],c1,c2,n,m;
void seth()//将A点,C点以及马能到的点初始化,加if以防出数组
{
sq[1][1]=1;
sq[c1+1][c2+1]=0;
if(c1>=0&&c1<=n+1&&c2+3>=0&&c2+3<=m+1)
sq[c1][c2+3]=0;
if(c1>=0&&c1<=n+1&&c2-1>=0&&c2-1<=m+1)
sq[c1][c2-1]=0;
if(c1+2>=0&&c1+2<=n+1&&c2+3>=0&&c2+3<=m+1)
sq[c1+2][c2+3]=0;
if(c1+2>=0&&c1+2<=n+1&&c2-1>=0&&c2-1<=m+1)
sq[c1+2][c2-1]=0;
if(c1+3>=0&&c1+3<=n+1&&c2+2>=0&&c2+2<=m+1)
sq[c1+3][c2+2]=0;
if(c1+3>=0&&c1+3<=n+1&&c2>=0&&c2<=m+1)
sq[c1+3][c2]=0;
if(c1-1>=0&&c1-1<=n+1&&c2+2>=0&&c2+2<=m+1)
sq[c1-1][c2+2]=0;
if(c1-1>=0&&c1-1<=n+1&&c2>=0&&c2<=m+1)
sq[c1-1][c2]=0;
}
int main()
{
cin>>n>>m>>c1>>c2;
seth();
for(int i=1;i<=n+1;i++)
{
for(int u=1;u<=m+1;u++)
{
sq[i][u]=sq[i-1][u]+sq[i][u-1];
seth();
}
}
cout<<sq[n+1][m+1];
return 0;
}
因为这个题昨天一次过了
所以这个代码没有怎么改,显得比较臃肿。
流感传染 思路
和上个题相似,但这次不同的是这次要判断上下左右四个方向的房间,还要判断是否为空
但是多加几个判断谁不会啊
为了防止超出数组范围,我还是做了判断
这个题我估计解法不少
这里随便放一种解法
流感传染 代码
#include<iostream>
#include<cstring>
using namespace std;
char s[110];
int a[110][110];
struct nxx
{
int r;
int c;
int d;
}q[10100];
int nexe[][2]={{-1,0},{1,0},{0,-1},{0,1}};
int main()
{
int n,m;
int h=1,t=1;
int r,c,d;
int nr,nc,gt=0;
int i,j;
cin>>n;
for(i=0;i<n;i++)
{
cin>>s;
for(j=0;j<n;j++)
if(s[j]=='.')
a[i][j]=0;
else if(s[j]=='@')
{
a[i][j]=1;
q[t].r=i;
q[t].c=j;
q[t].d=1;
t++;
}
else if(s[j]=='#')
a[i][j]=2;
}
cin>>m;
while(h<t)
{
r=q[h].r;
c=q[h].c;
d=q[h].d;
if(d==m)
break;
for(i=0;i<4;i++)
{
nr=r+nexe[i][0];
nc=c+nexe[i][1];
if(a[nr][nc]==0&&0<=nr&&nr<n&&0<=nc&&nc<n)
{
q[t].r=nr;
q[t].c=nc;
q[t].d=d+1;
a[nr][nc]=1;
t++;
}
}
h++;
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(a[i][j]==1)
gt++;
cout<<gt<<endl;
return 0;
}
这个解法是用了数组来判断周围四个房子是否为空/已经被感染
移动路线 思路
啊这题一看就非常的眼熟,这不就是过河卒的简化+反向版吗
过河卒是只能向下和向右,这个题蚂蚁只能向上和向右
我的主题思路还是用二维数组来推导每个方格的可能路径总数
实际上就是把过河卒的每个格由上+左改为下+左
(甚至如果想偷懒的话就改一下数组下标,删掉关于马的定点就行)
就不多说了
移动路线 代码
#include <iostream>
using namespace std;
int sq[21][21],m,n;
int main()
{
cin>>m>>n;
sq[1][1]=1;
for(int i=1;i<=m;i++)
{
for(int u=1;u<=n;u++)
{
sq[i][u]=sq[i-1][u]+sq[i][u-1];sq[1][1]=1;
}
}
cout<<sq[m][n]<<endl;
return 0;
}
本组题总结
要会数形结合,注意不变点
T 1 1 8 8 斐 波 那 契 数 列 (2) + T 1 1 8 9 P e l l 数 列 + T 1 1 9 6 踩 方 格
啊那为什么把这三道题放在一起呢?
因为他们都是找规律数列递推题
斐波那契数列(2) 思路
啊那这为什么是(2)呢?
因为它多加了个取模1000......
思路就很简单了,毕竟斐波那契数列在这里只用到递推公式了
即对于i>=3
j[i]=j[i-1]+j[i-2]
再加上模1000
j[i]=j[i-1]+j[i-2]%1000
当然在这里一个一个模也是可以的
斐波那契数列(2) 代码
#include <iostream>
using namespace std;
int long long f[10000001],num[10000001],a;
int main()
{
int n;
cin>>n;
for(int u=0;u<n;u++)
{
cin>>a;
f[1]=f[2]=1;
for(int i=3;i<=a;i++)
{
f[i]=(f[i-1]+f[i-2])%1000;
}
num[u]=f[a];
}
for(int i=0;i<n;i++)
cout<<num[i]<<endl;
return 0;
}
极 其 简 单
Pell数列 思路
看题之前:看起来好高级的样子
看题之后:真高级,这不就斐波那契数列第一项x2吗
Pell数列 代码
#include <iostream>
using namespace std;
int long long f[10000001],num[10000001],a;
int main()
{
int n;
cin>>n;
for(int u=0;u<n;u++)
{
cin>>a;
f[1]=1;
f[2]=2;
for(int i=3;i<=a;i++)
{
f[i]=(2*f[i-1]+f[i-2])%32767;
}
num[u]=f[a];
}
for(int i=0;i<n;i++)
cout<<num[i]<<endl;
return 0;
}
踩方格 思路
说实话我最一开始以为这也是个图形问题
后来发现这个好像没有界限就不是很好推,于是就一点一点的写,然后发现:
这不也是Pell数列吗......
(真就套娃)
踩方格 代码
#include <iostream>
using namespace std;
int main()
{
int x[21]={0},n;
x[0]=1;
x[1]=3;
cin>>n;
for(int i=2;i<=n;i++)
{
x[i]=2*x[i-1]+x[i-2];
}
cout<<x[n];
return 0;
}
本组题总结
耐心找规律,鬼都能做对
总结
可以发现,到了递推,这些题都有或许难度了,也不再是只是狭窄的考法,算法的思路也逐渐拓宽,那这更需要我去耐心思考,看到题就用笔和纸分析一下,不要纯靠想
也可以去Dfkuaid/ZYTHONC的回顾那看看
Dfkuaid
ZYTHONC
End
2020.2.2
3882词
9404字符


 浙公网安备 33010602011771号
浙公网安备 33010602011771号