入门到入土 | Master Theorem

「0.0」序言

最近做初赛题，发现这些小学数学题真是一个都不会（

发现基本上每年都要考主定理，于是在这里简单记录一下。

「1.0」Master Theorem

主定理主要适用于求解形如下面这个递归式的时间复杂度：

\[T(n)=aT(\frac{n}{b})+f(n) \]

其中参数的含义如下：

• \(n\) 是问题规模大小。

• \(a\) 是原问题子问题的个数。

• \(\dfrac{n}{b}\) 是每个子问题的大小，当然这里的前提是设所有子问题的大小相等。

• \(f(n)\) 是分拆子问题和合并子问题的（时间）复杂度函数。

不过就我做的这几年的提高组初赛题来看，参数的意义实际上不太考，一般都是直接给出柿子让你分析时间复杂度。

「1.1」情况分类

下面的大小比较都是渐进意义上的。

上式的复杂度分析主要如下列三种情况：

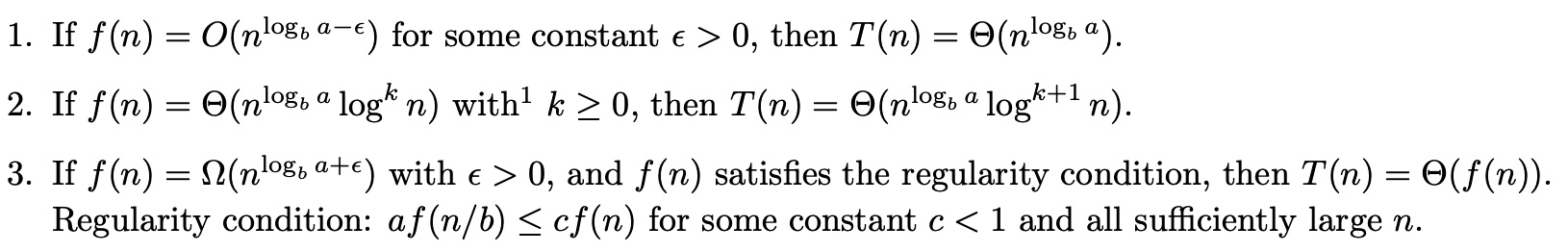
当然也有简化的版本（不与上面的三种一一对应）：

1. 若 \(f(n) > \Theta(n^{\log_ba})\) 且对于足够大的 \(n\) 和常数 \(c<1\) 有 \(af(\frac{n}{b}) \le cf(n)\)，那么 \(T(n) = \Theta(f(n)).\)

2. 若 \(f(n) < \Theta(n^{\log_ba})\)，则 \(T(n) = \Theta(n^{\log_ba}).\)

3. 若 \(f(n) = \Theta(n^{\log_ba}\log^kn)\)，则 \(T(n) = \Theta(n^{\log_ba}\log^{k+1}n)\).

「2.0」例题分析

「2.1」Binay Search

Stop learning useless algorithms, go and solve some problems, learn how to use binary search.

显然我们每次把一个问题分成两个子问题，所以 \(a=1,b=2\)，即：

\[T(n)=T(\frac{n}{2})+\Theta(1) \]

因为 \(\Theta(n^{\log_21}) = \Theta(1)\)，所以复杂度为 \(T(n) = \Theta(n^{\log_21}\log^1n) = \Theta(\log n).\)

「2.2」归并排序

和二分查找类似，不过原问题的子问题个数为两个，故 \(a=2\)，同时合并子问题的时间复杂度为 \(\Theta(n)\)，即：

\[T(n)=2T(\frac{n}{2})+\Theta(n) \]

因为 \(\Theta(n^{\log_22}) = \Theta(n)\)，所以复杂度为 \(T(n) = \Theta(n\log n).\)

「2.3」NOIP 2016TG

假设某算法的计算时间表示为递推关系式：

\[T(n) = 2T(\frac{N}{4})+sqrt(n),T(1) = 1. \]

则算法的时间复杂度为（ ）。

因为 \(\Theta(n^{\log_42}) = \Theta(\sqrt n)\)，所以 \(T(n) = \Theta(\sqrt n \log n).\)

「2.4」NOIP 2017TG

假设某算法的计算时间表示为递推关系式：

\[T(N) = 2T(\frac{N}{2})+N\log N,T(1) = 1. \]

则算法的时间复杂度为（ ）。

因为 \(\Theta(N^{\log_22}) = \Theta(N)\) 且 \(k=1\) 时 \(\Theta(N\log N) = \Theta(N \log^k N)\)，所以 \(T(N) = \Theta(N\log^2N).\)

「2.5」浴谷 SCP21 初赛

为了维护 CCF 的知识产权利益，本次比赛简称 SCP 第一轮。

假设某算法的计算时间表示为递推关系式：

\[T(n) = 3T(\frac{n}{2})+\Theta(n),T(1) = \Theta(1). \]

则算法的时间复杂度为（ ）。

因为 \(\Theta(n^{\log_23}) > \Theta(n)\)，所以 \(T(n) = \Theta(n^{\log_23}).\)

「3.0」尾声

明天就是 CSP-S1 2021 了，希望各位都 RP++，AK 初赛（

希望我能进复赛（