初见 | 数据结构 | 李超线段树

前言

单纯的学了一下而已（

因为尚未深入进行研究所以曰之浅学浅记。

本次浅记就主要根据洛谷 P4097 [HEOI2013]Segment 这道模板题来浅曰之，题目描述略。

思路

从一个相对好切入的点开始，实际上李超线段树某种程度上可以自己发明（？

首先看到这个题，会发现我们需要一个 DS 来维护这样一个线段的“容器”，它需要完成如题的各项操作。

比较显然的是我们在每个区间内维护一个在本区间每个值都取值最大的线段的编号，那么我们就需要线段树来维护这个东西。

那么考虑如何在每次插入线段的时候都能让每个区间保持最优，有两个步骤：

1. 这个区间是线段的定义域的子集，即 \([L,R] \in D.\)

2. 将此线段和当前区间内最优线段进行比较以让该区间保持最优。

第一个步骤很好实现，那么考虑第二个，如何去比较呢？

我们考虑让一个线段加入的影响通过不断二分区间来分化下传，下面来分类讨论之：

假设我们新加入的直线/线段为 \(f\)，原有最大值为 \(g\)，区间中点为 \(mid.\)

1. \(f\) 斜率大于 \(g:\)

   • 如果 \(f(mid)>g(mid)\)，那么 \(f\) 在右子区间一定最优，而 \(g\) 仍有可能在左子区间更优。
     

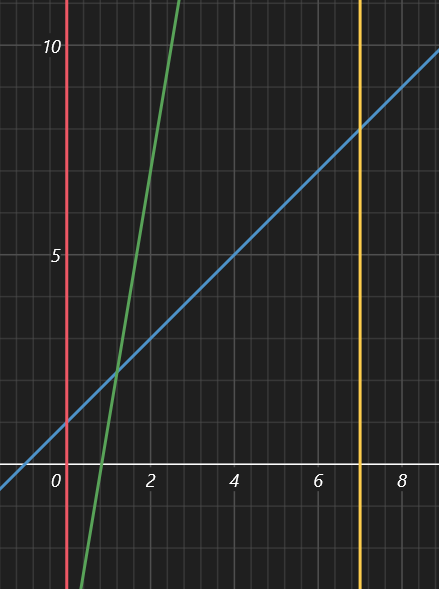
   • 反之，\(g\) 在左子区间一定最优，而 \(f\) 仍有可能在右子区间更优。
     

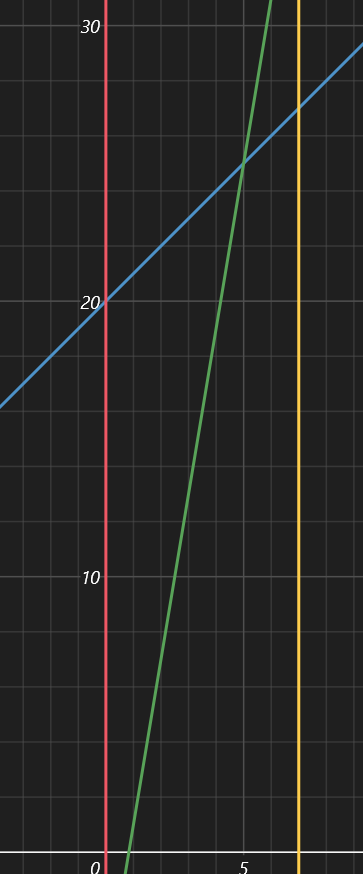
2. \(g\) 斜率大于 \(f:\)

   • 如果 \(f(mid)<g(mid)\)，那么 \(f\) 在左子区间一定最优，而 \(g\) 仍有可能在右子区间更优。
     

   • 反之，\(g\) 在右区间一定最优，而 \(f\) 仍有可能在左子区间更优。
     

还有一些特殊情况，比如说形如 \(f(x) = d\)（\(d\) 为常数）的直线/线段，我们将其缩到每次的比较点来方便对比（

当然，在比较的时候还需要考虑编号的大小，所以我们在比较的时候，将编号小的稍微加一点点（EPS）来保证我们每次得到的是编号更小的最优选择。

然后就可以上代码了，复杂度的话，瓶颈在于 Pushdown 为 \(O(\log n)\)，于是查询和修改的操作都为 \(O(\log ^2n)\)，总体复杂度就是 \(O(n \log ^2n).\)

Code

#include <iostream>
#include <stdio.h>
#include <cmath>
#include <algorithm>
#include <cstring>

#define Heriko return
#define Deltana 0
#define Romanno 1
#define S signed
#define LL long long
#define DB double
#define R register
#define I inline
#define CI const int
#define CL const long long
#define mkp(a,b) make_pair(a,b)
#define mst(a,b) memset(a,b,sizeof(a))
#define ON std::ios::sync_with_stdio(false);cin.tie(0)
#define Files() freopen("RNMTQ.in","r",stdin);freopen("RNMTQ.out","w",stdout)

using namespace std;

template<typename J>
I void fr(J &x) {
    short f(1);
    x=0;
    char c(getchar());

    while(c<'0' or c>'9') {
        if(c=='-')
            f=-1;
        
        c=getchar();
    }

    while(c>='0' and c<='9') {
        x=(x<<3)+(x<<1)+(c^=48);
        c=getchar();
    }
   
    x*=f;
}

template<typename J>
I void fw(J x,bool k) {
    if(x<0)
        x=-x,putchar('-');

    static short stak[35];
    short top(0);

    do {
        stak[top++]=x%10;
        x/=10;
    }
    while(x);

    while(top)
        putchar(stak[--top]+'0');

    k?puts(""):putchar(' ');
}

template<typename J>
I J Hmax(const J &x,const J &y) {
    Heriko x>y?x:y;
}

template<typename J>
I J Hmin(const J &x,const J &y) {
    Heriko x<y?x:y;
}

CI MXX(1e5+1),MOD1(39989),MOD2(1e9);
const DB EPS(1e-12);

I void Hmod(int &x,int y,int mod) {
    x=(x+y-1>=mod)?x+y-mod:x+y;
}

#define lc(x) (x<<1)
#define rc(x) (x<<1|1)

struct Line {
    DB k,b;
    int id;

    Line(const DB &k=0,const int &x=0,const int &y=0,const int &id=0) : k(k),b(y-x*k),id(id){}

    I DB Calc(int x) {
        Heriko k*x+b;
    }

    I bool Empty() {
        Heriko !id;
    }
}

t[MXX<<2];

I void Hswap(Line &x,Line &y) {
    Line z;
    z=x,x=y,y=z;
}

I Line Lmx(Line x,Line y,int v) {
    Heriko x.Calc(v)>(y.Calc(v)+((x.id>y.id)?EPS:-EPS))?x:y;
}

void Pushdown(int x,int l,int r,Line v) {
    int mid((l+r)>>1);

    if(t[x].Empty())
        t[x]=v;
    else {
        if(v.Calc(mid)>t[x].Calc(mid)+(v.id>t[x].id?EPS:-EPS))
            Hswap(v,t[x]);

        if(v.Calc(l)>t[x].Calc(l))
            Pushdown(lc(x),l,mid,v);
        else if(v.Calc(r)>t[x].Calc(r))
            Pushdown(rc(x),mid+1,r,v);
    }
}

void Modify(int x,int lx,int rx,Line v,int l=1,int r=MXX) {
    if(lx<=l and r<=rx)
        Heriko Pushdown(x,l,r,v);

    int mid((l+r)>>1);

    if(lx<=mid)
        Modify(lc(x),lx,rx,v,l,mid);
    
    if(rx>mid)
        Modify(rc(x),lx,rx,v,mid+1,r);
}

Line Query(int x,int pos,int l=1,int r=MXX) {
    if(l==r)
        Heriko t[x];

    int mid((l+r)>>1);

    if(pos<=mid)
        Heriko Lmx(t[x],Query(lc(x),pos,l,mid),pos);
    else
        Heriko Lmx(t[x],Query(rc(x),pos,mid+1,r),pos);
}

int n,lmd,lstans,cnt;

S main() {
    Files();

    fr(n);

    while(n--) {
        int opt;
        fr(opt);

        if(!opt) {
            int x1;
            fr(x1),Hmod(x1,lmd,MOD1);
            fw((lstans=Query(1,x1).id),1);
            lmd=lstans%MOD1;
        }
        else {
            int x1,x2,y1,y2;
            Line v;
            fr(x1),fr(y1),fr(x2),fr(y2);
            Hmod(x1,lmd,MOD1),Hmod(x2,lmd,MOD1);
            Hmod(y1,lstans,MOD2),Hmod(y2,lstans,MOD2);

            if(x1>x2)
                x1^=x2^=x1^=x2,y1^=y2^=y1^=y2;

            if(x1==x2)
                v.b=Hmax(y1,y2),v.id=++cnt;
            else
                v=Line(1.0*(y2-y1)/(x2-x1),x1,y1,++cnt);
            
            Modify(1,x1,x2,v);
        }
    }

    Heriko Deltana;
}