初见 | 图论 | Tarjan

「启」

之前一直没空写，NOIP 考前重新学了一下，虽然考场上完全没用到就是了。

这篇可能晚一点同步到 github，因为 WTG 上没有把 Hexo 配置好。

大概按照 OI-Wiki 来简单写一点。

「Pre」

首先是一些前置知识。

「强连通分量」

在有向图 \(G\) 中强连通是指 \(G\) 中的任意两个节点联通，强连通分量则是极大的强连通子图。

强连通分量的英文是 Strongly Connected Components，简称 SCC.

「DFS 搜索树」

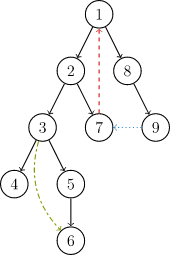
除了普通的树边之外，DFS 搜索树中还有可能出现以下三种类型的边：

1. 回边（红），即指向祖先结点的边。

2. 横叉边（蓝），即边的另一端是一个已经遍历过，但不是当前结点祖先的点。

3. 前向边（绿），搜索时遇到一个子树中的结点生成的。

那么在这颗搜索树中求 SCC，有以下的性质：

设结点 \(x\) 为某个 SCC 在搜索树中遇到的第一个结点，那么这个 SCC 的剩余结点一定是搜索树中以 \(x\) 为根的子树中。

可以反证证明：设有一个结点 \(y\) 在当前 SCC 中但是不在搜索树中以 \(x\) 为根的子树中，那么 \(x\) 到 \(y\) 的路径上一定有一条离开子树的边，即存在一条横叉边或者回边，然而根据定义发现两条边要求指向的结点是被访问过的，这和 \(x\) 的定义矛盾，得证。

「Tarjan」

Tarjan 主要是为每个结点 \(x\) 维护了两个变量：dfn[x] 和 low[x].

前者表示在 DFS 时 \(x\) 被遍历到的次序，后者表示 \(x\) 能回溯到的 dfn 最小的栈中的结点。显然的是后者可以用未访问过的子树中的结点 \(y\) 的 low[y] 来更新，否则用 dfn[y] 更新。

「Code」

之前的模板库里放了个栈用 vector 的，这里再放一个手写栈的，缺省源使用 「V5.2」.

template <typename J>
I J Hmin(const J &x,const J &y)
{
    Heriko x<y?x:y;
}

CI MXX(5e4+1),NXX(1e4+1);

int n,m;

struct Node
{
    int nex,to;
}

r[MXX];

int rcnt,head[NXX];

I void Add(int x,int y)
{
    r[++rcnt]=(Node){head[x],y};
    head[x]=rcnt;
}

int dfn[NXX],low[NXX],dfsid,stak[NXX],top,sz[NXX],scc[NXX],scctot;

bitset<NXX> instak;

void Tarjan(int x)
{
    low[x]=dfn[x]=++dfsid;
    stak[++top]=x,instak[x]=1;

    for(int i(head[x]);i;i=r[i].nex)
    {
        int y(r[i].to);

        if(!dfn[y])
        {
            Tarjan(y);
            low[x]=Hmin(low[x],low[y]);
        }
        else if(instak[y])
            low[x]=Hmin(low[x],dfn[y]);
    }

    if(dfn[x]==low[x])
    {
        ++scctot;

        while(stak[top]!=x)
        {
            scc[stak[top]]=scctot;
            ++sz[scctot];
            instak[stak[top]]=0;
            --top;
        }

        scc[stak[top]]=scctot;
        ++sz[scctot];
        instak[stak[top]]=0;
        --top;
    }
}

「终」

不知道啥时候写游记（