总之就是 | ZROI CSP联测 Day6
「启」
虽然最终的结果是涨一点点了 rating,但实际上是前几次保灵垫出来的(
实际上这是最惨淡的一次 ZROI-CSP 测试。
除了正解,有时候会把我考场想到的一些东西扔到这里面。
缺省源使用「V5」.
「A」聚会
可以说是手速题,但是因为自己过于自信忘了看自己写的复杂度是多少痛失 60 pts.
「A」题目简述
给定一个长度为 \(n \ (n \le 5 \times 10^5)\) 的 \(01\) 序列,求所有位置到其最近的 \(1\) 的距离之和。
「A」思路简述
首先是我场上完全没有意识到自己写的是 \(O(n^2)\) 的惨淡思路……
「A」40 pts
我一开题,本着手速题不能多吃罚时的理念,随便敲了一个就交上去没再管,而且后来拍了拍也是对的,就没管。(然而对拍的数据远不及 \(5 \times 10^5\))
大体的思路就是对于每一个 \(0\) 分别去左右找离它最近的 \(1\),复杂度是 \(O(n^2).\)
「A」100 pts
正解显然不是 \(O(n^2)\) 这种连 60 pts 都没有的垃圾算法。
实际上最一开始做的时候也想到这个了,但是阴差阳错就没写这个(
思路很简单,就算分别从左往右和从右往左求出 \(l_i\) 和 \(r_i\),分别代表左右离 \(i\) 最近的 \(1\) 的距离。
「A」Code
依次是 \(40\) 和正解。
「A」40 Code
template<typename J>
I J Hmin(const J &x,const J &y) {Heriko x<y?x:y;}
CI MXX(5e5+1);
int T,n;
char s[MXX];
S main()
{
fr(T);
for(int t(1);t<=T;++t)
{
fr(n);scanf("%s",s+1);LL ans(0);
for(int i(1);i<=n;++i)
if(s[i]=='0')
{
int step(0),temp(0x3f3f3f3f);
while(i-step>=1)
{
++step;
if(s[i-step]=='1')
{
temp=step;break;
}
}
step=0;
while(i+step<=n)
{
++step;
if(s[i+step]=='1')
{
temp=Hmin(step,temp);break;
}
}
ans+=temp;
}
printf("Case #%d: %lld\n",t,ans);
}
Heriko Deltana;
}
「A」AC Code
template<typename J>
I J Hmin(const J &x,const J &y) {Heriko x<y?x:y;}
CI MXX(5e5+1),INF(0x3f3f3f3f);
int T,n,l[MXX],r[MXX];
char s[MXX];
S main()
{
Files();
fr(T);
for(int t(1);t<=T;++t)
{
fr(n);scanf("%s",s+1);
LL ans(0);mst(l,0x3f);mst(r,0x3f);
int lstone(-1);
for(int i(1);i<=n;++i)
if(s[i]=='1') lstone=i;
else
{
if(lstone==-1) l[i]=INF;
else l[i]=i-lstone;
}
lstone=-1;
for(int i(n);i;--i)
if(s[i]=='1') lstone=i;
else
{
if(lstone==-1) r[i]=INF;
else r[i]=lstone-i;
}
for(int i(1);i<=n;++i)
if(s[i]=='0')
ans+=Hmin(l[i],r[i]);
printf("Case #%d: %lld\n",t,ans);
}
Heriko Deltana;
}
「B」跳房子
构造题,为什么最近总是考构造题(
想了半天找不到构造规律,最后交了个随机化跑路了……
「B」题目简述
现有 \(n \ (n \le 1000)\) 个格子和 \(3\) 个人,每个格子 \(i\) 有其权值 \(x_i \ (x_i \le 10^{18})\),保证序列 \(x\) 是严格递增的。
每一对格子 \((a,b)\) 必须三个人里的一个人。
现在每个人开始跳房子,一个人可以从 \(i\) 跳到 \(j\),当且仅当:
-
\(i < j;\)
-
\((i,j)\) 属于这个人;
-
\(x_i | x_j.\)
现在要对每一对格子 \((a,b)\) 进行分配,使得:不管从哪个位置出发,都不会有一个人连续跳三次以上。
「B」思路简述
说实话看了题解之后才发现这个构造如此巧妙(
我们设 \(f(x)\) 表示 \(x\) 在二进制表示下为 \(1\) 的最高位。
然后把除以 \(4\) 相同的一对位置分给第一个人,除以 \(16\) 相同的一对位置分给第二个人,剩下的给第三个人。
因为对于每一对 \((a,b)\),有 \(a|b , a < b \Rightarrow a \le 2b\),所以对于每个分配,组内都不会超过四个。
对于求 \(f(x)\),我们只需要不断地将 \(x\) 右移一位直到 \(x\) 只剩下一位即可。
「B」Code
CI MXX(1001);
int n;
LL a[MXX],f[MXX];
I LL FstOne(LL x)
{
LL res(0);
while(1)
{
x>>=1;++res;
if(x==1) break;
else if(!x) {--res;break;}
}
Heriko res;
}
S main()
{
fr(n);
for(int i(1);i<=n;++i) fr(a[i]);
for(int i(1);i<=n;++i) f[i]=FstOne(a[i]);
for(int i(2);i<=n;puts(""),++i)
for(int j(1);j<i;++j)
if((f[i]/4)==(f[j]/4)) fw(1,0);
else if((f[i]/16)==(f[j]/16)) fw(2,0);
else fw(3,0);
Heriko Deltana;
}
「C」人结
谢谢已经结在一起了。
「C」题目简述
圆上有 \(n\) 个点,按照顺时针标号,每个点与两个点相连,要求通过移动点在圆上的位置,使得最终的边没有交叉的一个环。
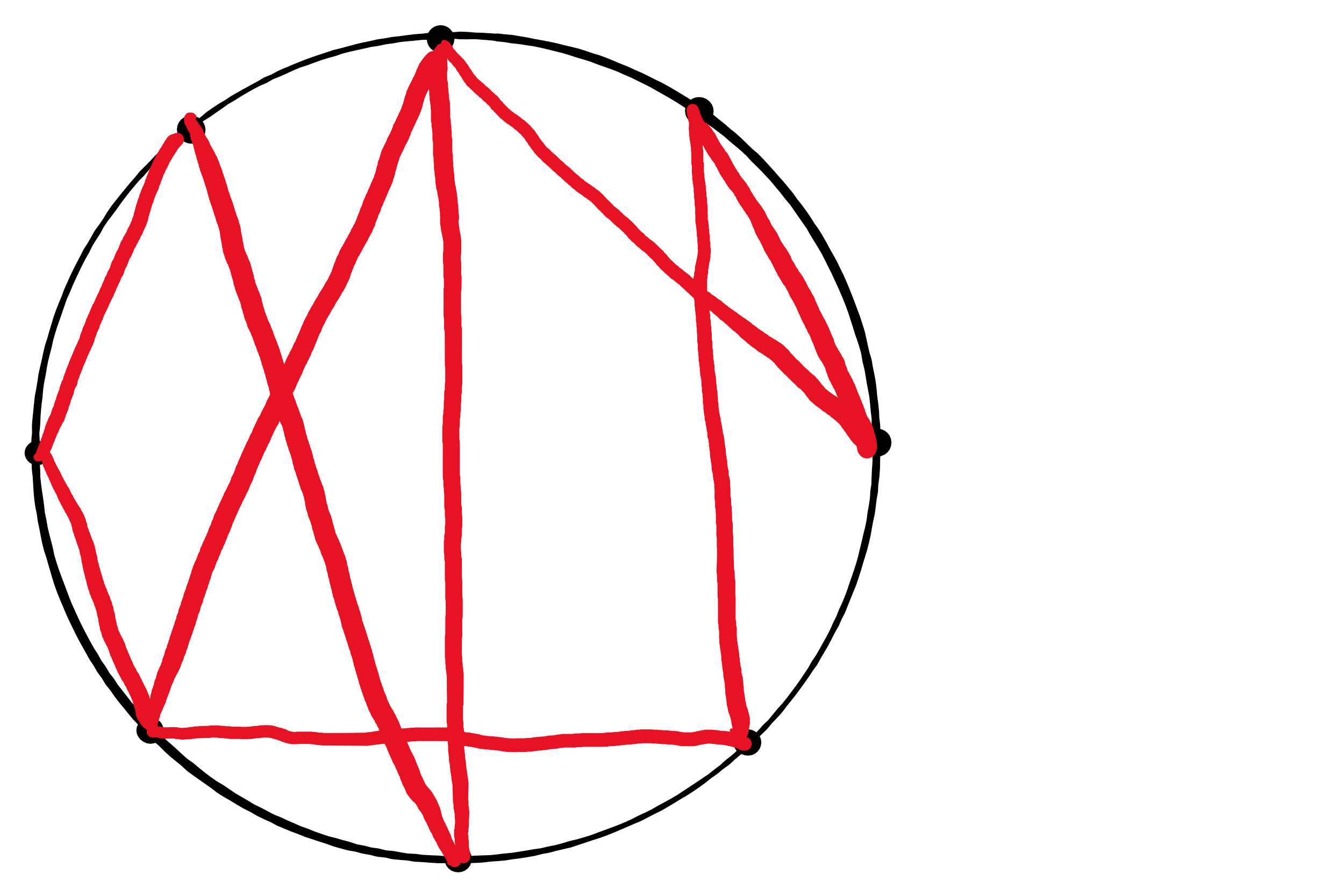
「C」思路简述
当且仅当整张图不连通的时候无解,所以我们先找个环,找不到乆无解。
然后断环为链之后做一遍 LIS,做一遍 LCS,这里是翻转了数组做了两遍 LIS.
「C」Code
template<typename J>
I J Hmax(const J &x,const J &y) {Heriko x>y?x:y;}
CI MXX(501);
int n,a[MXX];
struct Node
{
int nex,to;
}
r[MXX<<1];int cnt,head[MXX];
I void Add(int x,int y) {r[++cnt]=(Node){head[x],y};head[x]=cnt;}
bool vis[MXX];
int tot,ans;
void GetRing(int x)
{
vis[x]=1;a[++tot]=x;
for(int i(head[x]);i;i=r[i].nex)
if(!vis[r[i].to])
GetRing(r[i].to);
}
int f[MXX],q[MXX],tl;
I void LIS()
{
for(int i(1);i<=n;++i) a[i+n]=a[i];
for(int i(1);i<=n;++i)
{
mst(f,0),mst(q,0);tl=0;
for(int j(i);j<=i+n-1;++j)
{
if(a[j]>q[tl]) q[++tl]=a[j];
else q[lower_bound(q+1,q+tl+1,a[j])-q]=a[j];
f[j-i+1]=tl;
}
ans=Hmax(ans,f[n]);
}
}
S main()
{
Files();
while(1)
{
fr(n);
if(!n) break;
mst(vis,0),mst(head,0),mst(a,0);
cnt=tot=ans=0;
for(int i(1);i<=n;++i) {int x,y;fr(x),fr(y),Add(i,x),Add(i,y);}
GetRing(1);
if(tot!=n) {puts("Not solvable.");continue;}
else puts("Knot solvable.");
LIS();reverse(a+2,a+1+n);
LIS();fw(n-ans,1);
}
Heriko Deltana;
}
「D」辣椒
我剪不开辣椒,我是垃圾。
「D」题目简述
有 \(n\) 个辣椒,用 \(n−1\) 根绳子连接,所以每两个辣椒都可以通过一些绳子连接在一起。也就是说,它们形成一棵树。
现在要准备今天的三顿饭。为此,他将剪断两根绳子以得到三个较小的辣椒串,每餐一个。
当然,每一餐饭太辣是不好的,所以要选择尽量减少最大辣度辣椒串和最小辣椒串之间的大小差异,注意辣椒串的辣度就是辣椒串包含辣椒的个数。你需要寻求这个最小差异是多少。
「D」思路简述
\(O(n^2)\) 做法即为枚举两个点 \(x,y\),然后把这两个点连向父亲的边断掉,设 \(sz(x)\) 为以 \(x\) 为根的子树大小,则剩下的三部分大小有以下的情况:
-
\(y\) 是 \(x\) 的祖先,则三部分大小分别为:\(sz(x),sz(y)-sz(x),n-sz(y);\)
-
\(y\) 是 \(x\) 没有祖孙关系,那么为:\(sz(x),sz(y),n-sz(x)-sz(y).\)
然后维护从根到 \(x\) 上的路径的点的点集,从中找到一个点 \(z\) 使得 \(|sz(y) - \dfrac{n+sz(z)}{2}|\),用 set 维护,用 lower_bound() 查找,在深度变大的时候加入新点。同时维护一个已经处理过但是非 \(x\) 祖先的点集,在其中找到一点使得 \(|sz(y)-\dfrac{n-sz(z)}{2}|\),维护方式相同,当一个点被删除的时候,将其从直系集中取出,加入旁系集,总的时间复杂度为 \(O(n \log n).\)
「D」Code
template<typename J>
I J Hmax(const J &x,const J &y) {Heriko x>y?x:y;}
template<typename J>
I J Hmin(const J &x,const J &y) {Heriko x<y?x:y;}
CI MXX(5e5+1),INF(0x3f3f3f3f);
int n,ans(INF);
struct Node
{
int nex,to;
}
r[MXX];int cnt,head[MXX];
I void Add(CI &x,CI &y)
{
r[++cnt]=(Node){head[x],y};head[x]=cnt;
r[++cnt]=(Node){head[y],x};head[y]=cnt;
}
I int Dlt(CI &x,CI &y,CI &z) {Heriko Hmax(Hmax(x,y),z)-Hmin(Hmin(x,y),z);}
int sz[MXX];
void DFS1(int x,int fa)
{
sz[x]=1;
for(int i(head[x]);i;i=r[i].nex)
{
int y(r[i].to);
if(y==fa) continue;
DFS1(y,x);sz[x]+=sz[y];
}
}
set<int> s1,s2,cs1,cs2;
void DFS2(int x,int fa)
{
if(s1.size())
{
int pos(*s1.lower_bound((n+sz[x])>>1));
ans=Hmin(ans,Dlt(n-pos,sz[x],pos-sz[x]));
}
if(s2.size())
{
int pos(*s2.lower_bound((n-sz[x])>>1));
ans=Hmin(ans,Dlt(sz[x],pos,n-pos-sz[x]));
}
if(cs1.size())
{
int pos(*cs1.lower_bound(-((n+sz[x])>>1)));pos=-pos;
ans=Hmin(ans,Dlt(n-pos,sz[x],pos-sz[x]));
}
if(cs2.size())
{
int pos(*cs2.lower_bound(-((n-sz[x])>>1)));pos=-pos;
ans=Hmin(ans,Dlt(sz[x],pos,n-pos-sz[x]));
}
s1.insert(sz[x]),cs1.insert(-sz[x]);
for(int i(head[x]);i;i=r[i].nex)
if(r[i].to!=fa)
DFS2(r[i].to,x);
s1.erase(sz[x]),cs1.erase(-sz[x]);
s2.insert(sz[x]),cs2.insert(-sz[x]);
}
S main()
{
Files();
fr(n);
for(int i(1),x,y;i<n;++i) fr(x),fr(y),Add(x,y);
DFS1(1,0);DFS2(1,0);fw(ans,1);
Heriko Deltana;
}
「末」
6 Days Left.

 6 Days Left.
6 Days Left.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号