QBXT游记 | Day1 Afternoon

矩阵相关

基础知识的补充

上来先是讲了讲矩阵的基本知识，这些我在之前写的高斯消元里面的基本都有了，这里再补充一些我之前没记过的

• 0矩阵，就是指所有元素都为0的矩阵
• 单位矩阵，记作\(I\)，实际上就是一个特殊的对角矩阵，对角线上的元素都为1，实际上在矩阵当中的地位就如数字中的1一样，对了还有一点就是单位矩阵是\(n*n\)的

关于矩阵加速递推

我发现老师可能对这个班的认识有点偏差？上午问我们是不是不常用scanf，下午就觉得矩阵快速幂我们都会，还是我学的太不均衡了？

斐波那契相关

我们都知道斐波那契数列的递推公式是\(f_n=f_{n-1}+f_{n-2}\)，即使这是\(O(n)\)的柿子，但是很明显过于大的数据也是i处理不出来的，那么我们可以考虑使用矩阵来加速递推

设用如下的矩阵柿子来推导：

\[\begin{bmatrix}F_n&F_{n-1}\end{bmatrix}*\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}F_{n+1}&F_{n}\end{bmatrix} \]

那么根据矩阵乘法的定义，我们可以列出如下方程：

\[\begin{cases}F_{n+1}=F_{n}*a+F_{n-1}*c \\ F_{n}=F_{n}*b+F_{n-1}*d\end{cases} \]

很明显能看出对于第二个方程，\(b=1，d=0\)，因为左右都有\(F_n\)，保证系数统一即可

但是第一个方程没有这样的特点，怎么办呢？

我们可以根据斐波那契的递推公式来做一些拆解：

\[F_{n+1}=F_{n}*a+F_{n-1}*c =F_{n}+F_{n-1} \]

由此我们可以煺得\(a=c=1\)

但是单纯这样的做是不行的，这样的做法是\(0(n)\)还多带一个矩阵乘法的常数的

所以我们考虑拆开：(设上面那个加速递推的矩阵为B)

\[F_{0}+F_{1}*B*B*B*B*B*B\cdots*B=F_{n}+F_{n-1} \]

可以发现共用n-1个B，可以用矩阵快速幂，总的时间复杂度是\(O(\log n)\)的

下面是一个Q&A，有关斐波那契求和：

请问老师，今天在上课的时候求斐波那契的前n项的和时

您有说到把矩阵从\(\begin{bmatrix}F_n&F_{n-1}\end{bmatrix}\)扩展至\(\begin{bmatrix}F_n&F_{n-1}&S_{n}\end{bmatrix}\)，其中

\(S_{n}=\sum\limits_{i=0}^{n}F_i\)然后您写到一个柿子是\(S_{n+2}=S_{n+2}+S_{n}\)，请问这个柿子是如何推得的？

（也可能不是这个柿子？）

然后有位热心的大佬回复了我：

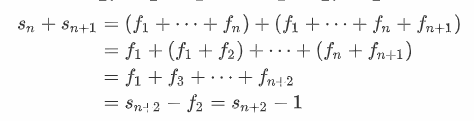
也就是说，S_{n+2}=S_{n+1}+S_{n}+1

今天的也就这些了，明天继续加油