基础算法 | 高精度 Simple
这一篇是我复习的时候用的,相比 初学时的那篇 更为精简
高精度算法
实际上快两个月过去了,这个也没用上几回。
主要就是针对大于C++能够处理的数据范围进行运算,主要思想是模拟
高精度加法
算法分析
上来一看,这个数据被拆分成了一个个位,按照模拟的思想,我们很容易就想到了早在小学就学习过的最基础的加法计算方法:列 竖 式

这个的基础就是两个数对应的每个数位相加,但是这样就涉及一个问题:进 位
不过这个还是挺简单的,两个一位数相加最多也就进1,于是我们马上就可以愉快地开始用代码实现了。
代码实现
首先是理一下思路
- 录入数据:用字符串/字符数组接收,再逆序存到int/float/double数组,以便于计算
这个地方倒序的原因是如果牵扯到进位,正序的话进位,下标要-1,要是第一个进位的话......
那数组会非常的开心,我也是。
于是用倒序,进位的时候下标+1,只要数组开的够长就好了,最后逆序输出就好了
需要注意的是,如果没有必要,我尽量不用vector
因为它倒序搞比较麻烦
-
进行加法运算:根据刚才算法分析中的用while循环完成就可以了(
虽然我个人比较喜欢用for,但是那样有麻烦了亿点) -
输出数据:因为是逆序输入,所以逆序输出。
以下是注释版代码
//高精度加法
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int a[201],b[201],c[201];//三个int数组来储存数据进行运算
int main()
{
char na[201],nb[201];
//两个用来接收数据的字符串(字符数组)
gets(na);
gets(nb);
//接收数据
int la=strlen(na);
int lb=strlen(nb);
//计算长度
for(int i=0;i<la;i++){
a[la-i]=na[i]-'0';
}
for(int i=0;i<lb;i++){
b[lb-i]=nb[i]-'0';
}
//将数据倒序存入
int lc=1,x=0;
//这里的x是进位的数 ,初始为0
while(lc<=la||lc<=lb){//这里算到不包括最后一次进位的最高位
c[lc]=a[lc]+b[lc]+x;//这里是a+b+进位数
x=c[lc]/10;//让进位数等于结果的十位
c[lc]%=10;//让此位结果变为初步结果的个位
lc++;//要计算的位数+1
}
//加法计算的核心,这里算到不包括最后一次进位的最高位
c[lc]=x;
//如果最后一次计算有进位数,让进位数等于新高位
if(c[lc]==0)
lc--;
//如果没有进位,那么把lc--以便输出
for(int i=lc;i>0;i--)
cout<<c[i];
cout<<endl;
//输出,收尾(
return 0;
}
精简版
//高精度加法
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int a[201],b[201],c[201];
int main()
{
char na[201],nb[201];
gets(na);
gets(nb);
int la=strlen(na);
int lb=strlen(nb);
for(int i=0;i<la;i++)a[la-i]=na[i]-'0';
for(int i=0;i<lb;i++)b[lb-i]=nb[i]-'0';
int lc=1,x=0;
while(lc<=la||lc<=lb)
{
c[lc]=a[lc]+b[lc]+x;
x=c[lc]/10;
c[lc]%=10;
lc++;
}
c[lc]=x;
if(c[lc]==0)
lc--;
for(int i=lc;i>0;i--)
cout<<c[i];
cout<<endl;
return 0;
}
高精度减法
算法分析
和加法一样,用列 竖 式的方法,这里只需要考虑不 够 减 要 借 位的问题。

那么具体的解决方法就是不够减的时候本位+10,上一位-1,非常简单
代码实现
理一下思路
-
录入数据:用字符串/字符数组接收,再逆序存到int/float/double数组,以便于计算
-
进行减法运算:
- 判断被减数是否小于减数,如果是的话交换顺序并先输出一个负号
- while+判断完成算法分析中分析到的借位问题
-
输出数据:因为是逆序输入,所以逆序输出。
(应该没有人发现我是复制的)
注释极其多版代码
//高精度减法
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int a1[256]={0},a2[256]={0},a[256]={0};
//声明来存数的数组
int main()
{
char n1[256],n2[256],m[256];//用于接收数据的字符串(字符数组),以及m这个后面用来交换用的中间量
gets(n1);
gets(n2);
//接收数据,这里默认是n1-n2
if((strlen(n1)<strlen(n2))||(strlen(n1)==strlen(n2)&&strcmp(n1,n2)<0))
//判断被减数是否小于减数
//第一个判断条件很好懂,是被减数的位数少于减数
//第二个是当两者位数相同时,使用strcmp进行比较
/*strcmp:
strcmp(n1,n2)就是从n1[0]和n2[0]开始比较(以ASCⅡ里的顺序来比较)
若前者大,则返回大于0的数
反之,返回小于0的数
若相同,则返回0
(这样理解,可能不准确,于是去问了下度娘:)
strcmp函数是string compare(字符串比较)的缩写,
用于比较两个字符串并根据比较结果返回整数。
基本形式为strcmp(str1,str2),若str1=str2,则返回零;
str1<str2,则返回负数;若str1>str2,则返回正数。
(嘛,还是差不多的)
*/
{
strcpy(m,n1);
strcpy(n1,n2);
strcpy(n2,m);
/*
strcpy就是用后者赋值给前者,复制贴贴
怕自己这个蒟蒻看不懂于是又去了一趟度娘(蒟蒻的日常)
strcpy,即string copy(字符串复制)的缩写。
strcpy是C++语言的一个标准函数 ,
strcpy把含有'\0'结束符的字符串复制到另一个地址空间,
返回值的类型为char*。
*/
cout<<"-";//先输出一个负号,这样后面就可以安心的运算了(蒟蒻发言)
}
int l1=strlen(n1),l2=strlen(n2);
for(int i=0;i<l1;i++)
a1[l1-i]=int(n1[i]-'0');
for(int i=0;i<l2;i++)
a2[l2-i]=int(n2[i]-'0');
//将数据存入int类型数组,不用多说
int x=1;
//x代表要计算的是第几位数
while(x<=l1||x<=l2)
{
if(a1[x]<a2[x])
{
a1[x]+=10;
a1[x+1]--;
}//这里的意思就是如果不够减就向高位借10,高一位-1,此位+10
a[x]=a1[x]-a2[x];
x++;
}
//减法核心程序
int l=x;
while(a[l]==0&&l>1)
l--;
//如果最高位是0,那么x--以免最高位是0
for(int i=l;i>=1;i--)
cout<<a[i];
cout<<endl;
//收尾(来自蒟蒻的喜悦,前几次没成功竟然是因为最后输出的时候打成i++了,果然是Dai)
return 0;
}
也就我能把这么基础的东西打75行了,自卑
精简版代码
//高精度减法
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int a1[256]={0},a2[256]={0},a[256]={0};
int main()
{
char n1[256],n2[256],m[256];
gets(n1);
gets(n2);
if((strlen(n1)<strlen(n2))||(strlen(n1)==strlen(n2)&&strcmp(n1,n2)<0))
{
strcpy(m,n1);
strcpy(n1,n2);
strcpy(n2,m);
cout<<"-";
}
int l1=strlen(n1),l2=strlen(n2);
for(int i=0;i<l1;i++)
a1[l1-i]=int(n1[i]-'0');
for(int i=0;i<l2;i++)
a2[l2-i]=int(n2[i]-'0');
int x=1;
while(x<=l1||x<=l2)
{
if(a1[x]<a2[x])
{
a1[x]+=10;
a1[x+1]--;
}
a[x]=a1[x]-a2[x];
x++;
}
int l=x;
while(a[l]==0&&l>1)
l--;
for(int i=l;i>=1;i--)
cout<<a[i];
cout<<endl;
return 0;
}
高精度乘法
算法分析
这个理解起来也比较简单。
和前面的思路差不多,我还是从列 竖 式入手
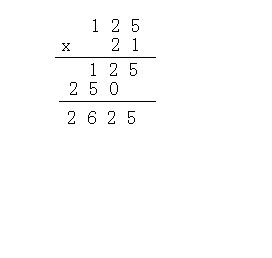
相信各位现在或许还时常能见到这个东西
我们根据竖式来算的话,就是用a[i]去乘b[1],b[2],b[3]...,然后每次i在变化的时候需要错位,这个还是比较好想的,
让接收答案的数组c的下标是c[内层循环变量+外层循环变量-1]即可。
还有一点就是,在进位的问题,这个也比较好解决。参照刚才加法的方法,可以声明一个变量x来代表每次进位的数,只不过这里不只是进位1了,而是最多进位9,
我们还是可以用当前结果/10的方法来完成计算进位的多少
代码实现
-
输入数据,和之前一样。
-
进行乘法运算
- 得到当前的数据,即本次乘积+上次计算结果(最初默认为0)+进位(默认为0)
- 用本次数据求出本次产生进位和本次数据最终结果(即%10)
-
逆序输出,和之前一样
这次分析的多了点,上代码
多理解还是很有用的(至少对我来说),理解了加和减,乘法也能触类旁通
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int a[256],b[256],c[256000],x=0;
int main()
{
char s1[256],s2[256];
scanf("%s",s1);
scanf("%s",s2);
int l1=strlen(s1),l2=strlen(s2);
for(int i=0;i<=l1-1;i++)
a[l1-i]=s1[i]-'0';
//没想到啊,查了15分钟错误,原来是这一行的s1[i]-0 打成了s1[i]=0
for(int i=0;i<=l2-1;i++)
b[l2-i]=s2[i]-'0';
//前边的就和高精度加减法一样
for(int i=1;i<=l1;i++)
{
x=0;
for(int p=1;p<=l2;p++)
{
c[i+p-1]=c[i+p-1]+x+(a[i]*b[p]);
//上次处理的数+进位+当前乘积
x=c[i+p-1]/10;
//x是进位数
c[p+i-1]%=10;
//当前结果取余10
}
c[l2+i]=x;
//当内循环结束后,当前进位是下一位
}
//这里是乘法核心程序,注解都在上面了,实际上结合高精度的加减法来说理解起来并不难
int l3=l1+l2;
while(c[l3]==0&&l3>1)
l3--;
for(int i=l3;i>=1;i--)
cout<<c[i];
cout<<endl;
//收尾>o<
return 0;
}
End
2021.3.19
实际上就是炒冷饭版,精简一下好查阅而已
不过回锅肉还是可以的嘛()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号