初见 | 图论 | 并查集 + Kruskal
经典咏流传~~
假设有 l 到 r,这是 l,这是 r。
这些边我不加。
这些边我不加!
暴力怎么做?暴力是不是!
加边,加边,加边,然后,并查集查询!
本文头文件
因为本人比较懒所以就一次性全写在这里了,没有很多
#include <bits/stdc++.h>
#define Heriko return
#define Deltana 0
#define LL long long
#define R register
#define I inline
#define S signed
using namespace std;
并查集
并查集,这个名字就让人感到很亲切啊,啊,啊,啊,啊那为什么呢
因为它字很少
因为根据字面意思就可以理解什么是并查集
甚至你可以用并查集的操作来理解并查集
并查集,拆开来看就是三个字,并.查.集,那么根据最后一个字我们很明显的能看出来这是一个类集合的数据结构
- 并,是指集合可以进行合并
- 查,是指可以查询元素所在的集合
那么并查集就是支持这两种操作的集合啦~
并查集的主要结构就是先将每一个元素作为单独的集合,再根据题意进行合并操作,最后查找目标元素在哪一个集合
一般来说我们用数组\(or\)链表的形式来实现并查集,由于数组形式比较常见,我在这里就只说一下数组的实现形式吧~
疯狂掩盖自己因为对链表不熟悉而不学链表的实现形式的Lazy实质
并查集实现
清单
-
初始化,将每一个元素作为一个单独的集合
-
实现查
-
实现并
初始化
一般来说,题目会给我们元素的个数\(n\),那么这里的每一个元素按照并查集的要求,需要先分割成一个个独立的集合
考虑到我们这里用数组实现,那么就用\(f[i]\)来表示\(i\)元素所在的集合,若用图/树的语言来说的话,就是用来表示\(i\)的父结点
由于最一开始每一个元素都是独立的一个集合,那么\(i\)的父亲\(f[i]\)就是\(i\)本身,因为当前这个集合只有它一个元素
于是乎我们在思路上完成了清单的第一个内容,下面是\(Code\)
for(R LL i=1;i<=n;i++) f[i]=i;//对于R LL 看不懂的可以看本篇博客头部放的头文件
为了有助于理解,我在这里再用图来解释一下:
假设这个\(n=6\),然后这个六个元素分别是:\(H , e , r , i , k , o\)
那么通过这一次初始化,我们就获得了如下的6个独立的集合

然后我们就可以开始下一步了
并
实际上并很简单,若让\(x∪y\),那么我们只需要让\(f[x]∪y\)即可,因为我们是数组实现的,所以我们只需要让\(f[x]=y\)即可,下面是\(Code\)
I void uni(R LL x,R LL y)
{
f[x]=y;
}
及其简单的小函数~
还是用图来形象理解一下,这里的并就相当于是让\(x\)和\(y\)的父节点相同:
还是上面那6个元素,我们进行uni(H,e)后变成这样:
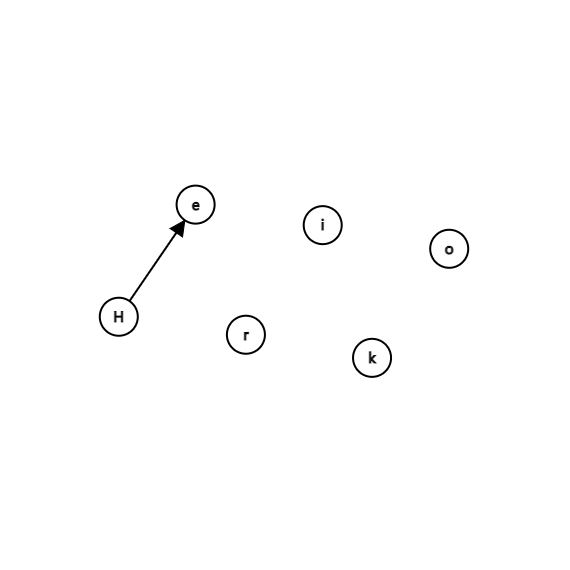
再uni(i,r)就变成了:
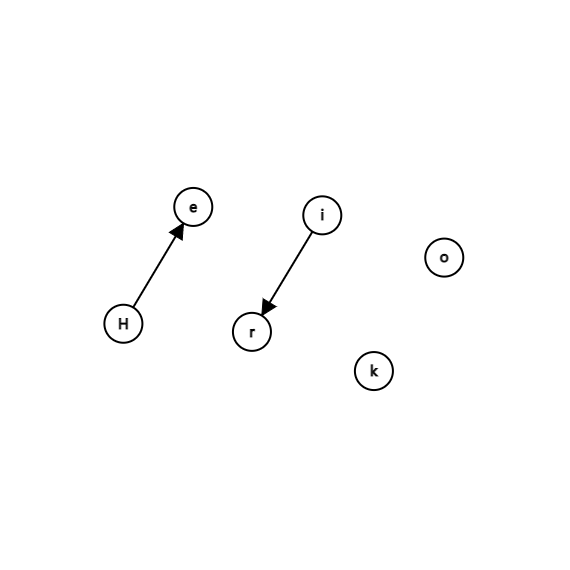
然后我们再进行uni(r,e) 和 uni(o,e):
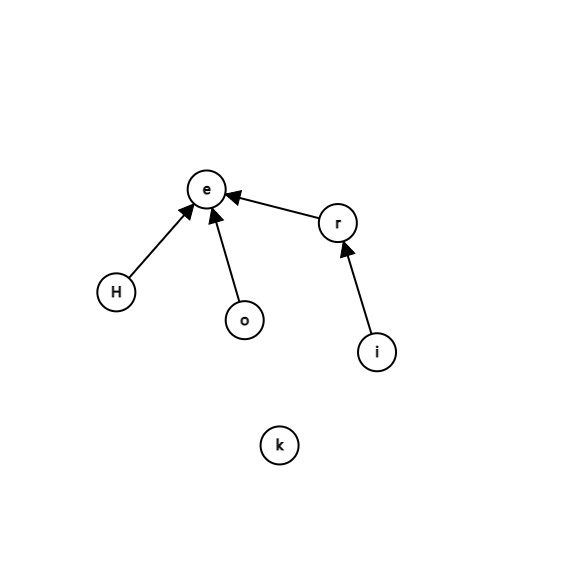
可怜的k没有人要,接下来,就要进行下一步力
查
类似于查家谱,这里查的是这个元素最头上的父节点,毕竟在并查集的世界里,你父亲的父亲,还是你父亲
那这里就要用到一个递归的函数,查\(x\)的父节点\(f[x]\),再查\(f[x]\)的父节点\(f[f[x]]\)......
一直到\(f[f[f[...f[x]...]]]=f[f[...f[x]...]]\)也就是它的父节点是他自己(我父亲竟是我自己),这个时候,就查到了\(x\)的最源头的父节点
那为什么是查到父节点等于自己就停下来呢?因为我们在初始化的时候让每个元素成为自己的父节点,所以当一个元素是最源头的时候,父节点就是他自己
I LL find(R LL x)
{
if(f[x]!=x) f[x]=find(f[x]);
Heriko f[x];
}
比如说如果我们要查这个\(H\),也就是要找\(f[H]\),那么我们就从find(H)
具体怎么找到的我就不画图了,可以直接参考上图
这样我们就完成了清单的全部内容,于是乎可以去做一些模板题,洛谷一搜就一堆
但是,你会发现,许多并查集的题目的标签旁边,还有着一个标签:最小生成树
至于原因,下面很快就会说到
最小生成树
实际上这里主要讲的是\(Kruskal\)算法,但是它毕竟是实现最小生成树的一种算法,所以这里就简单说一下最小生成树
而在说最小生成树之前,需要提一句与其相关的定理:
\(N\)个点用\(N-1\)条边链接成一个连通块,所形成的图形只可能是树,没有其他可能。
而最小生成树就是在一个图里面选\(N-1\)条权值最小的边连接\(N\)个结点所构成的树
那么它解决的问题类别就是:
解决如何用最小代价来实现用\(n-1\)条边连接\(n\)个点的问题
那么这里比较常用的算法有二:Prim和Kruskal
Prim
Prim主要还是经典的蓝白点思想,这里简单一提
清单
- 初始化,初始化所有当前白点到\(v\)点的距离\(min[v]\)
- 用当前的白点重新计算到各个蓝点的\(min\)
- 根据题意求\(ans\)
初始化
这里的\(MST\)是权值之和
\(min[v]\)=当前白点到v点的距离,初始为无限 / \(0x7fffffff\) / \(0x3f\)
\(min[1]=0\)
\(MST=0\)
判断是否为蓝点的bool数组\(is[1...n]=ture\)
Prim核心
for(R LL i=1;i<=n;i++)
{
k=0;
for(R LL j=1;j<=n;j++)
{
if(is[j] && min[j]<min[k])
{
k=j;
is[k]=false;
}
}
for(R LL j=1;j<=n;j++)
if(is[j] && min[j]>w[k][j]) min[j]=w[k][j];
}
计算MST
for(R LL i=1;i<=n;i++) MST+=min[i];
这个算法的时间复杂度呢,是\(O(N^2)\)
那么下面就是\(Kruskal\)力
Kruskal
这个算法就是贪心策略+并查集,时间复杂度\(O(E log E)\),E是边数
大体思路就是先按照升序排序边的权值,然后......
加边加边加边,并查集查询
清单
- 存下来边的权值以及端点
- 排序
- 初始化。因为要用到并查集,所以显然所有的结点的父亲是自己
父亲竟是我自己++ - 因为要用到并查集,所以并查集的函数我们也要声明
- 主干,加边
加边加边直到树已经生成
存边
由于大部分的题的范围不允许我们开多维数组,于是乎我们开结构体
struct node
{LL x,y,z;}a[114514];
排序
由于我们用了结构体,所有我们如果要用sort的话,要么重载一下\(<或>\)要不然就写一个cmp函数
由于我太菜了导致重载用不习惯,所以下面就用声明函数的方法
I LL cmp(R LL a,R LL b)
{
Heriko a.z<b.z;
}
//在主函数里:sort(a+1,a+1+m,cmp); 即可
初始化
这里和并查集一样
for(R LL i=1;i<=n;i++) f[i]=i;
并查集的函数们
I LL find(R LL x)
{
if(f[x]!=x) f[x]=find(f[x]);
Heriko f[x];
}
I void uni(R LL x,R LL y)
{
R LL fx=find(x);
R LL fy=find(y);
f[fx]=fy;
}
猪肝 主干部分
for(R LL i=1;i<=n;i++)
{
if(find(a[i].x)!=find(a[i].y))
{
uni(a[i].x,a[i].y);//如果当前边i连接的两点还未连接,那么将两者并起来
k++;MST++;//k是已经加上的边数
}
if(k==n-1) break;//若已经加上了n-1条边,说明最小生成树已经生成
}
printf("%lld",MST);
这里为什么两者为连接就认定当前边是最小边呢?
这里和我们的贪心策略有关,由于我们在前面已经排序,所以若这两点还未有直接或间接的连接路径(也就是说这两者不在同一个连通块里)那么当前的这条边一定是将两点相连的最短边
那么这里再提供一份完整版的\(Kruskal\)求最小生成树,是实现洛谷P3366 最小生成树模板的\(Code\)
CODE
#include <bits/stdc++.h>
#define Heriko return
#define Deltana 0
#define LL long long
#define R register
#define I inline
using namespace std;
struct wood
{
int x,y,z;
}g[1000015];
int n,m,f[1000015],ln,ans;
I int find(R int a)
{
if(f[a]!=a) f[a]=find(f[a]);
Heriko f[a];
}
I void uni(R int a,R int b)
{
R int la=find(a);
R int lb=find(b);
f[la]=lb;
}
I int cmp(wood a,wood b)
{
Heriko a.z<b.z;
}
signed main()
{
scanf("%d%d",&n,&m);
for(R int i=1;i<=n;i++) f[i]=i;
for(R int i=1;i<=m;i++) scanf("%d%d%d",&g[i].x,&g[i].y,&g[i].z);
sort(g+1,g+1+m,cmp);
for(R int i=1;i<=m;i++)
{
if(find(g[i].x)!=find(g[i].y))
{
uni(g[i].x,g[i].y);
ln++;
ans+=g[i].z;
}
if(ln==m-1) break;
}
printf("%d",ans);
Heriko Deltana;
}
于是乎,我好像写完了!
End
话说为什么我觉得洛谷上好多黄的最小生成树题比绿的还难


 浙公网安备 33010602011771号
浙公网安备 33010602011771号