总之就是 | NOIOL PJ 题解
NOI Online 入门组
正如我预估的一样,我NOIO 入门炸了,才125pts,但是题解还是要稍微写一写的,毕竟也是一次比赛的经验
但是题(尤其是T3)我可能说不太明白,所以文字叙述呈递减态且少的可怜
T1 Cake
作为入门组的第一题,CCF还是很良心的
思路
这道题上来一看就知道绝对不是什么高级算法/数据结构等
而是一道纯特判分类讨论的题目
设\(ans\)为答案,再由于 \(a,b,c\) 等价,我们不妨设 \(a≤b≤c\)
-
首先观察可得:\(a=b=0\)时:一次都不用切,因为在\(a\)和\(b\)两人都不要的情况下,\(c\)要多少都可以
也就是说\(ans=0\)
-
接下来就是\(a=0\)时,有两种情况:
- \(b=c\),任意切一刀即可,即\(ans=1\)
- \(b≠c\),因为是任意选取角度,所以实际上两刀是可以切除全部的比例的,即\(ans=2\)
-
然后就是最一般的情况,\(a,b,c≠0\),有如下情况:
- \(a=b/b=c/a=c\),因为我们可以任意切角度,所以我们可以先切两部分相同的,然后剩下的那一份给那个不同的
- \(a+b=c\),切两刀,把两份不同的给\(b和a\),然后把剩下的两块给\(c\),保证\(a+b=c\)即可
- \(a\ne b\ne c\),切三刀,三刀可以切出任意比例的三份(证明我不是太会,于是推荐洛谷的第一篇题解)
代码
(由于是考场代码所以可能比较凌乱)
#include <bits/stdc++.h>
#define Heriko return
#define Deltana 0
#define LL long long
#define R register
#define I inline
using namespace std;
LL a,b,c,n,sum;
I LL gcd(LL a,LL b)
{
if(b==0) Heriko a;
else Heriko gcd(b,a%b);
}
signed main()
{
freopen("cake.in","r",stdin);
freopen("cake.out","w",stdout);
scanf("%lld",&n);
for(R LL i=1;i<=n;i++)
{
scanf("%lld%lld%lld",&a,&b,&c);
if((a==0 && b==0) || (b==0 && c==0) || (c==0 && a==0))
{
printf("0\n");
continue;
}
else if((a==0 && b==c) || (b==0 && a==c) || (c==0 && a==b))
{
printf("1\n");
continue;
}
else if((a==0 && b!=c) || (b==0 && a!=c) || (c==0 && a!=b))
{
printf("2\n");
continue;
}
LL k1=gcd(a,b);
LL k2=gcd(b,c);
LL k=gcd(k1,k2);
a/=k;b/=k;c/=k;
sum=a+b+c;
if(a+b==c || b+c==a || c+a==b || a==b || b==c || c==a)
{
printf("2\n");
continue;
}
printf("3\n");
}
fclose(stdin);
fclose(stdout);
Heriko Deltana;
}
T2 Pacman
这道题我直接嘤嘤嘤,小模拟题,加上一点数学(颅内)计算,正解早就想出来了,可惜写不完,我嘤嘤嘤嘤嘤嘤
果然还是我太菜了
思路
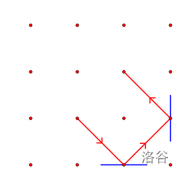
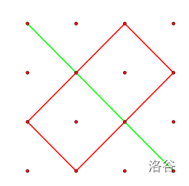
我就直接拿原题的图来说了,很明显我们能看出来:
因为\(Pacman\)在遇到墙(边界)时会镜面反射
所以,实际上对于 \(n*n\) 的矩阵点来说,一共只有\(n\)种路线
这\(n\)条路线实际上就是从第一行的第\(1-n\)个点放置\(Pacman\)的路线
(当然从最底边放也是一样的,总之只需要考虑\(n\)种情况)
于是乎我们就可以预处理这\(n\)条路线的得分
然后枚举任意两条路线进行计算即可,当然,要把重合的点去掉
于是乎就可以得出本题的核心思路:
- 预处理路线
- 枚举路线求最大值
啊,对,就这么好想,但是预处理的时候的镜面反弹和枚举路线时的求重合点对我来说有点毒
本来我脑子转的就慢,所以我只写完了预处理,最后只能提交一个有部分分的程序
那么下面就直接放上\(Code\),对于镜面反射和求重合点的部分推荐画图辅助理解
代码
- PS:回家打完之后到洛谷上面提交只有85pts,经过手模比较大的点矩阵发现是求重合点错了,于是乎看了看题解,这里的
repeat函数正是借鉴了一篇题解,而下面注释掉的是我的写法
#include <bits/stdc++.h>
#define Heriko return
#define Deltana 0
#define LL long long
#define R register
#define I inline
using namespace std;
LL n,a[1015][1015],num[1015],ans;
bool vis[1015][1015];
I int repeat(int x,int b)
{
if((b-x)%2) Heriko Deltana;
if(x==1 && b==n) Heriko a[(n+1)/2][(n+1)/2];
if(x==1) Heriko a[(b+1)/2][(b+1)/2]+a[(2*n-b+1)/2][(2*n-b+1)/2];
if(b==n) Heriko a[(n-x)/2+1][(n+x)/2]+a[(n+x)/2][(n-x)/2+1];
Heriko a[(x+b)/2][(b-x)/2+1]+a[(b-x)/2+1][(x+b)/2]+a[n-(b-x)/2][n-(x+b)/2+1]+a[n-(x+b)/2+1][n-(b-x)/2];
}
signed main()
{
memset(vis,false,sizeof(vis));
scanf("%lld",&n);
for(R LL i=1;i<=n;i++)
for(R LL j=1;j<=n;j++)
scanf("%lld",&a[i][j]);
for(R LL i=1;i<=n;i++)
{
if(i==1)
{
for(R LL j=1;j<=n;j++) num[i]+=a[j][j];
continue;
}
else if(i==n)
{
for(R LL j=n;j>=1;j--) num[i]+=a[n-j+1][j];
continue;
}
LL z=i-1;
for(R LL j=i;j<=n;j++) num[i]=num[i]+a[j-z][j]+a[j][j-z];
LL x=n+n-z;
for(R LL j=n-1;j>x-n;j--) num[i]=num[i]+a[x-j][j]+a[n-(x-j)+1][n-j+1];
}
for(R LL i=1;i<=n;i++)
{
for(R LL j=i;j<=n;j++)
{
if(i!=j && !vis[i][j])
{
vis[i][j]=vis[j][i]=true;
LL temp=num[i]+num[j];
if(n<=2)
{
ans=max(temp,ans);
continue;
}
if(n==3 && i==1 && j==n)
{
ans=max(temp-a[2][2],ans);
continue;
}
// if((i-j)%2==0)
// {
// LL x1=1+(abs(i-j))/2,y1=(i+j)/2;
// LL x2=n+1-x1,y2=n+1-y1;
// // printf("(%lld,%lld) (%lld,%lld) (%lld,%lld) (%lld,%lld)\n",x1,y1,y1,x1,x2,y2,y2,x2);
// temp=temp-a[x1][y1]-a[x2][y2];
// if(x1!=y1) temp=temp-a[y1][x1];
// if(x2!=y2) temp=temp-a[y2][x2];
// }
ans=max(temp-repeat(i,j),ans);
}
}
}
printf("%lld",ans);
Heriko Deltana;
}
T3 Ball
思路
说实话这道题想起来比较好想,但是在考场上我实现出来的可能性比较小
主要思路就是DFS爆搜大法师,因为每次进行操作之后,两个球都只会到边缘或者障碍的周围四个点,所以只有障碍的周围四个点和边缘-1的点是有意义的,所以最后状态只有2000左右,两层循环的话\(10^6\)的数据是能接受的
然后就让能互相到达的点之间建立边,最后顺着边推
这里推荐一个我赛后参考的博客:Watertomato的T3题解
下面就直接放代码了
代码
#include <bits/stdc++.h>
#define Heriko return
#define Deltana 0
#define S signed
#define LL long long
#define R register
#define I inline
using namespace std;
I void fr(LL &x)
{
LL f=1;char c=getchar();
x=0;
while(c<'0'||c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=(x<<3)+(x<<1)+c-'0';
c=getchar();
}
x*=f;
}
const int MXN=305,MXM=2005,MXX=1e5+5;
struct line
{
LL to,nex;
};
line e[MXX];//边
LL f[MXN][MXN],dis[MXM][MXM],name[MXN][MXN],t[MXM][MXM][5];
LL n,m,q,cnt,head[MXM][5],tot,x,y,X1,X2,Y1,Y2;
queue<pair<LL,LL> > que;
I void ADD(R LL x,R LL y,R LL z)
{
e[++cnt].to=y;
e[cnt].nex=head[x][z];
head[x][z]=cnt;
}
I bool CHECK(R LL x,R LL y)
{
if(f[x-1][y] || f[x+1][y] || f[x][y+1] || f[x][y-1]) Heriko true;
Heriko false;
}
I LL DIST(R LL X1,R LL Y1,R LL X2,R LL Y2)
{
Heriko min(dis[t[X1][Y1][0]][t[X2][Y2][0]],min(dis[t[X1][Y1][1]][t[X2][Y2][1]],min(dis[t[X1][Y1][2]][t[X2][Y2][2]],dis[t[X1][Y1][3]][t[X2][Y2][3]])));
}
S main()
{
fr(n),fr(m),fr(q);
for(R LL i=1;i<=m;i++)
{
fr(x),fr(y);
f[x][y]=1;
}
for(R LL i=1;i<=n;i++) f[0][i]=f[i][0]=f[n+1][i]=f[i][n+1]=1;
for(R LL i=1;i<=n;i++) for(R LL j=1;j<=n;j++) if(!f[i][j] && CHECK(i,j)) name[i][j]=++tot;
for(R LL i=1;i<=n;i++)
{
for(R LL j=1;j<=n;j++)
{
if(f[i][j-1]) t[i][j][0]=name[i][j];
else t[i][j][0]=t[i][j-1][0];
if(f[i-1][j]) t[i][j][1]=name[i][j];
else t[i][j][1]=t[i-1][j][1];
}
}
for(R LL i=n;i;i--)
{
for(R LL j=n;j;j--)
{
if(f[i][j+1]) t[i][j][2]=name[i][j];
else t[i][j][2]=t[i][j+1][2];
if(f[i+1][j]) t[i][j][3]=name[i][j];
else t[i][j][3]=t[i+1][j][3];
}
}
for(R LL i=1;i<=n;i++) for(R LL j=1;j<=n;j++) if(name[i][j]) for(R LL u=0;u<=3;u++) ADD(t[i][j][u],name[i][j],u);
for(R LL i=1;i<=tot;i++) for(R LL j=1;j<=tot;j++) dis[i][j]=1e9+7;
for(R LL i=1;i<=tot;i++) que.push(make_pair(i,i)),dis[i][i]=1;
while(!que.empty())
{
pair<LL,LL> temp=que.front();
que.pop();
for(R LL u=0;u<=3;u++)
{
for(R LL i=head[temp.first][u];i;i=e[i].nex)
{
for(R LL j=head[temp.second][u];j;j=e[j].nex)
{
LL qwq=e[i].to,qaq=e[j].to;
if(dis[qwq][qaq]==1e9+7)
{
dis[qwq][qaq]=dis[temp.first][temp.second]+1;
que.push(make_pair(qwq,qaq));
}
}
}
}
}
for(R LL i=1;i<=q;i++)
{
fr(X1),fr(Y1),fr(X2),fr(Y2);
if(X1==X2 && Y1==Y2) printf("0\n");
else
{
LL ans=DIST(X1,Y1,X2,Y2);
if(ans>=1e9) printf("-1\n");
else printf("%lld\n",ans);
}
}
Heriko Deltana;
}
End
总的来说,这次没爆0,差强人意吧
反映出来一个问题,就是头脑不灵活不敏捷,导致一个早就想出解法的题因为脑子转得慢直接85pts->25pts,确实不应该
只能祝自己\(CSP\) \(2021\) \(RP++\)了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号