初见 | 图论 | 入门概念

图论初步

图

简单的来说,用点和边连起来就叫做图,是一种数据结构.

图的分类

• 有向图:图的边有方向,两个节点之间只有一条有方向的边
• 无向图:图的边没有方向,也就是两个节点之间的路径是双向的

图的一些基本概念

• 结点的度:无向图中所有与当前结点相邻的边的数目

• 结点的入度:有向图中以当前结点为终点(即边所指的方向)的有向边的数目

• 结点的出度:有向图中以当前结点为起点的有向边的数目

• 权值:即边的费用,一般为长度

• 连通:如果图中结点U,V之间有能使U通向V的路径(可以是多条边的组合),那么就说U,V是连通的

  (注意:有向图中,这里的U和V是有方向的,如:1→2,那么说1和2连通,但2和1不连通)

• 回路:起点和终点相同的路径,或者叫做:环

图的储存结构

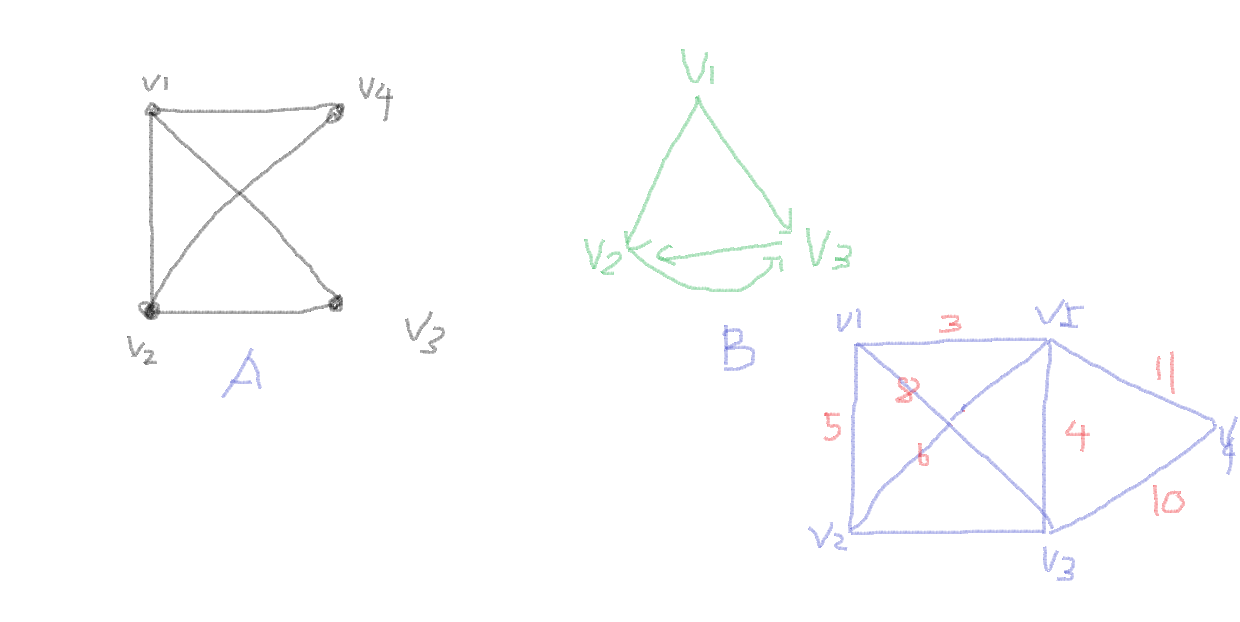
鼠标画画属实难受,漫画九级直接归宗了

二维数组邻接矩阵

int G[i][i]

这里的i是结点个数,将上图分别来表示

0 1 1 1

1 0 1 1

1 1 0 0

1 1 0 0

(第一个)

0 1 1

0 0 1

0 1 0

(第二个)

0 5 8 0 3

5 0 2 0 6

8 2 0 10 4

0 0 10 0 11

3 6 4 11 0

(第三个)

在二维表中有向图和无向图的边与表的关系

有向图中边数==非0数字数

无向图中边数==非0数字数/2

图的遍历

分为DFS和BFS

代码:

(这里包括一种结构体的声明图的方法)

#include <bits/stdc++.h>
using namespace std;
struct Node
{
	int Value;
	Node *Left;
	Node *Right;
	Node(int value=0,Node *left=NULL,Node *right=NULL):Value(value),Left(left),Right(right) {};//创建新的结点 
};Node *node[11];
inline void creat()
{
	node[1]=new Node(1);
	node[2]=new Node(2);
	node[3]=new Node(3);
	node[4]=new Node(4);
	node[5]=new Node(5,node[1],node[2]);
	node[6]=new Node(6,node[3],node[4]);
	node[7]=new Node(7);
	node[8]=new Node(8,node[5],node[6]);
	node[9]=new Node(9,node[7]);
	node[10]=new Node(10,node[8],node[9]);
}
inline void DFS(Node *Root)
{
	cout<<Root->Value<<' '; 
	if(Root->Left!=NULL)
		DFS(Root->Left);
	if(Root->Right!=NULL)
		DFS(Root->Right);
	return;
}
inline void BFS(Node *Root)
{
	queue<Node*> q;
	Node *temp;
	q.push(Root);
	while(!q.empty())
	{
		temp=q.front();
		cout<<temp->Value<<' '; 
		if(temp->Left!=NULL)
			q.push(temp->Left);
		if(temp->Right!=NULL)
			q.push(temp->Right);
		q.pop();
	}
	printf("\n");
}
int main()
{
	creat();
	Node *Root=node[10];
	printf("DFS:");
	DFS(Root);
	printf("\n");
	printf("BFS:");
	BFS(Root);
	printf("\n");
	return 0;
 } 

实际上这个就是一个二叉树

大约就是长这个样子

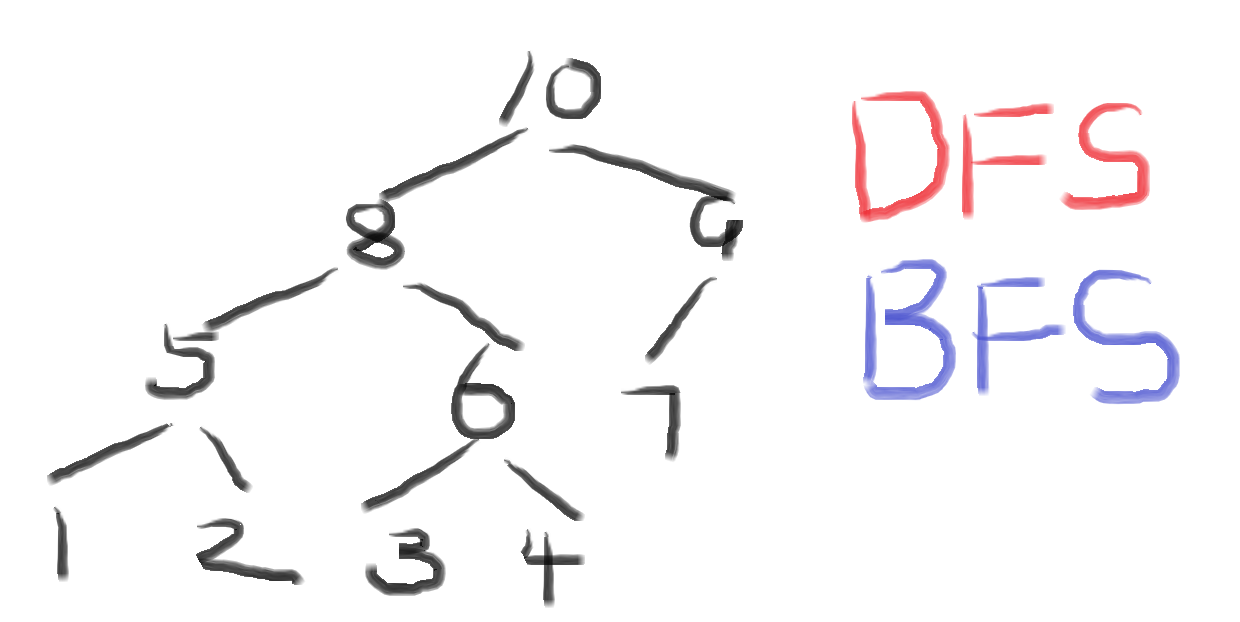
DFS相当于二叉树的先序遍历

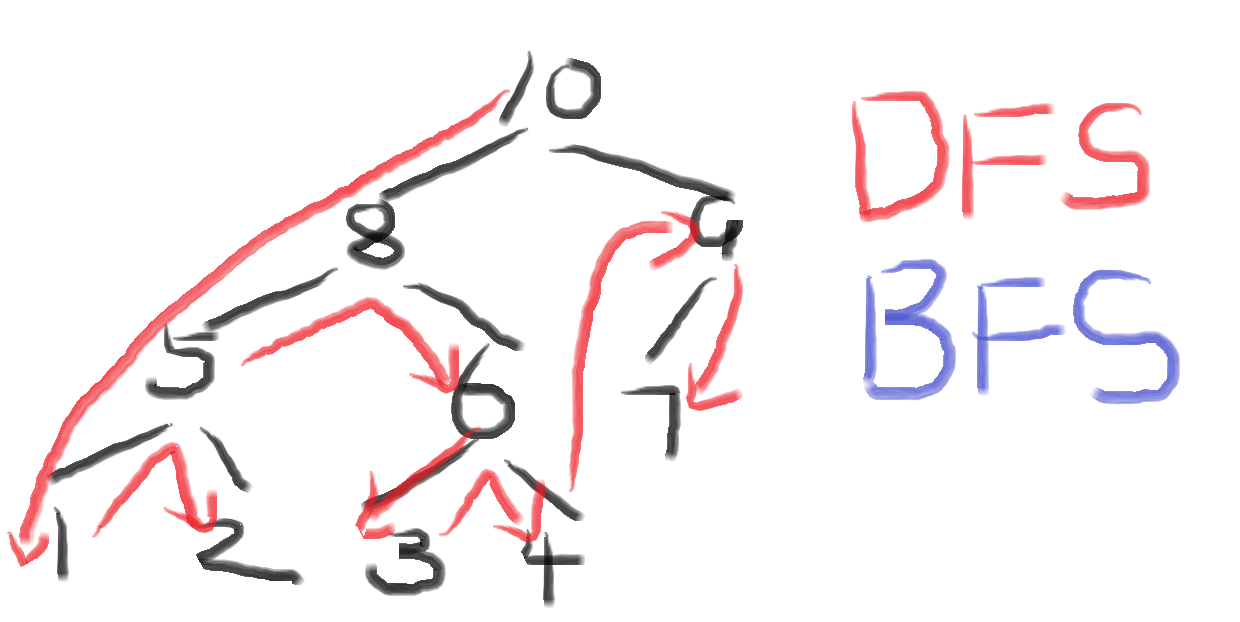
而BFS......就是普通的博法师

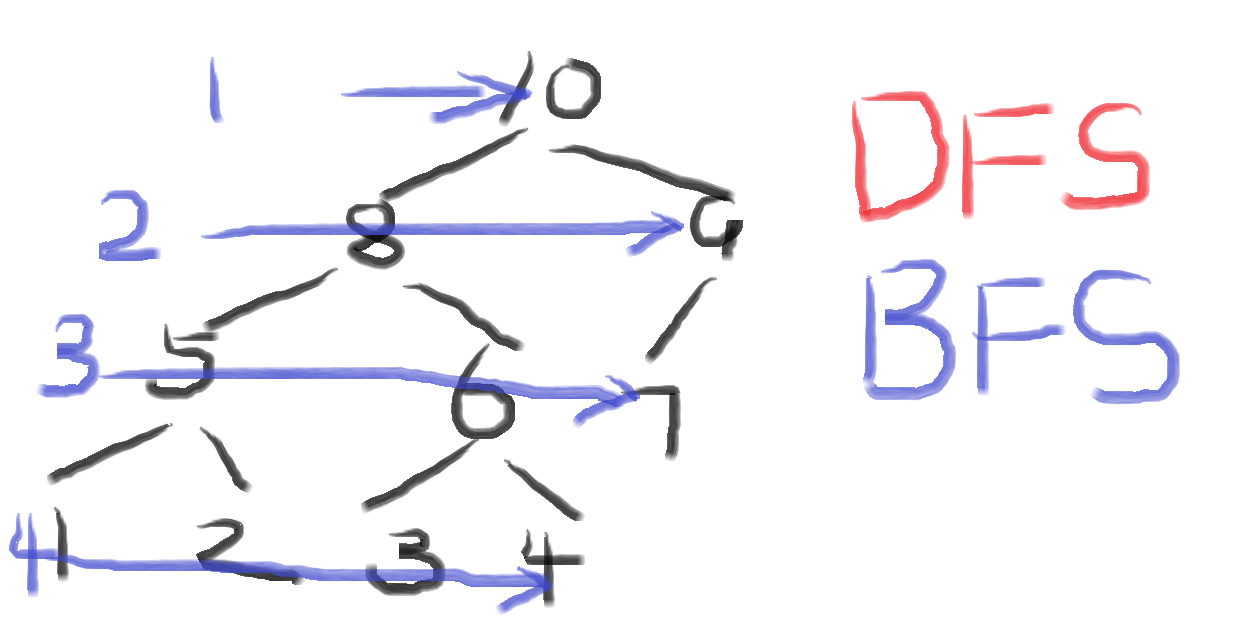
鼠标画图,敬请谅解

End Blog & 14

这里只是图论的初步

纪念14岁最后一天专属:
Also End 14