学习笔记（12）wqs 二分
（终于在马不停蹄的联考间喘息了一天，于是可以写一点总结）
在 \(max0810\) 的帮助下总算是解决了机房的老大难问题，想着为了防止遗忘，不如就地写一篇博客了事
（内容大量参考网络以尽量确保理解，如有冒犯望告知删改）
（主要参考的是这篇博客）
引入
\(wqs\) 二分最早由王钦石在2012年的集训队论文里系统地提出，又叫做“带权二分”，一般用于针对 \(Dp\) 凸完全单调性的优化
一般来说，\(wqs\) 二分通常被用来解决类似于以下形式的问题：
给定 \(n\) 个物品，要求从中选恰好 \(m\) 次，最大/最小化权值和
正常人应该可能大概会试着用 \(Dp\) 去搞搞，例如设 \(f[i][j]\) 表示考虑到第 \(i\) 个物品，已经选了 \(j\) 次的最大权值（以求最大值为例），那么容易得出转移方程有：
显然这会是一个 \(O(nm)\) 及以上的转移，而发现在把第二维 \(m\) 的限制去掉之后可以利用单调队列或者其他高科技轻松地做到 \(O(n)\) 处理。随后打个表发现 \((i, f[n][i])\) 的点对的拟合函数图像构成一个上凸包，很难不令人怀疑会有特殊的优化方法（当然确实也有除 \(wqs\) 以外的各种方法），这时便可以考虑使用 \(wqs\) 二分降维优化
原理
\(wqs\) 二分要求最优答案一定要与被限制的一维信息构成凸包（上凸还是下凸无所谓），这与其优化原理及做法息息相关
记 \(g[i]\) 表示 \(f[n][i]\)，观察 \((i, g[i])\) 构成的凸包的样子，有 \(x\) 轴表示选物品的次数， \(y\) 轴表示该次数下的最优答案（仍然以最大为例）：
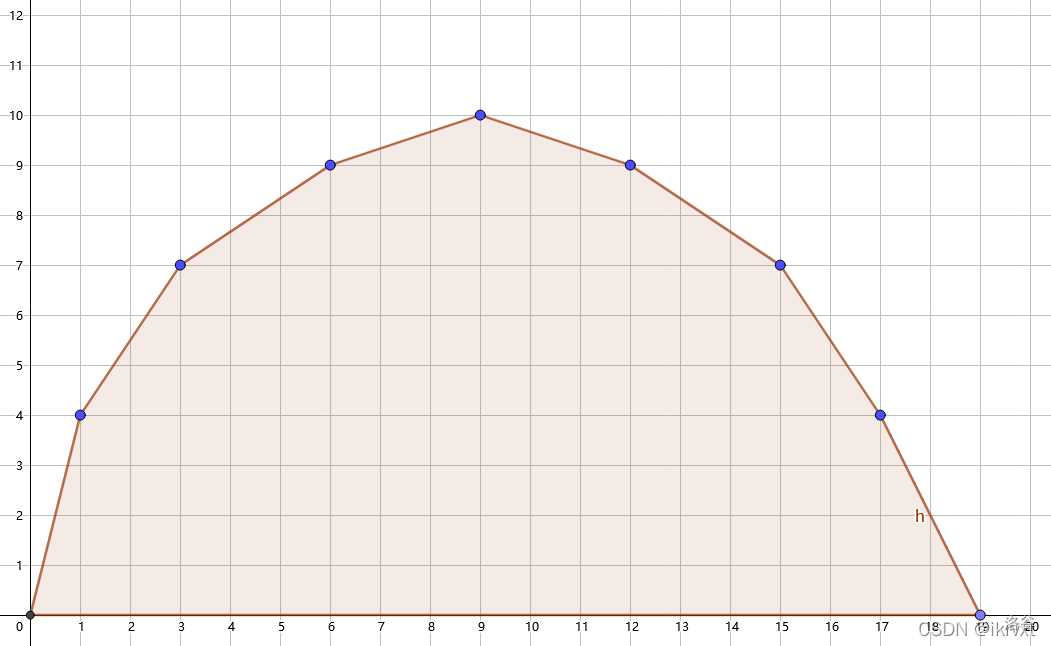
显然答案即 \(g[m]\)，但现在问题在于不能快速的计算 \(g[i]\)，不过我们能够知道这个凸包长什么样
考虑用一条直线 \(y = kx + b\) 去截取这个凸包，得到的切点表示该最优答案下选物品的次数以及最优答案：
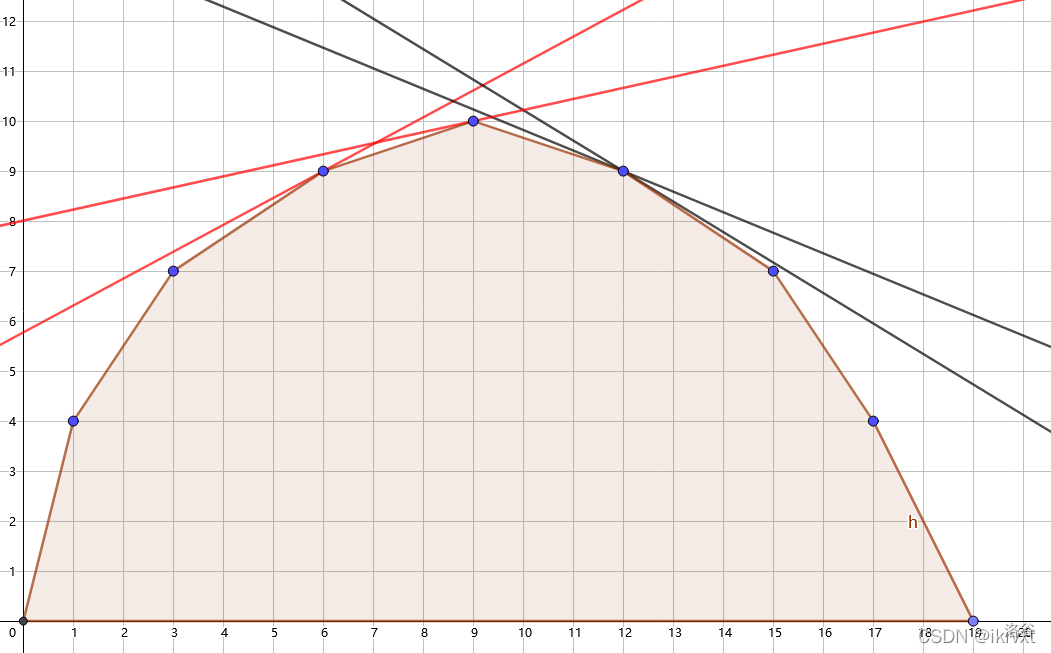
由于每个切点对应着一个选取次数下的最优答案，于是我们通过调整斜率 \(k\)，可以得到选取次数不同时的“最优答案”，而由于 \(g[x]\) 的斜率单调，因此直线斜率 \(k\) 可以二分，同时切点的纵坐标 \(y = g[x]\)，截距 \(b = y - kx\)，于是我们可以得到截距与最优答案的关系 \(b[x] = g[x] - k * x\)
而这个式子等价于把每一个选择获得的权值和 \(-=k\)，然后选任意次物品的最大权值和
这种去掉限制的问题一般就更加方便求解了
于是我们二分的直线斜率 \(k\) 就表示了我们二分的额外选择代价，而二分中的检查函数所计算的不考虑限制的 \(Dp\) 值表示直线的截距，根据检查函数计算出的实际选取次数（有二分的斜率 \(k\) 和直接 \(dp\) 算出来的 \(x,b\) ，原来的 \(g[x]\) 可以直接 \(b += k * x\) 算出来）来决定指针的移动
历史遗留问题
于是当时的机房同学照着模板去写了[国家集训队] Tree I这道题，然后成功遇到了一系列的蜜汁细节问题：
- 例如二分返回判断时是该用 \(\leq m\) 还是 \(\geq m\) 来移动指针？
- 二分额外代价时该加还是该减（当然这是定义问题了，\(wqs\) 二分默认处理的是上凸包的情况，根据定义就该是减了，可证这样处理下凸包也是正确的）？
- 二分到相同斜率的点该怎么选？
按照当时从题解区学来的方法发现是相同贡献的情况下“要优先选黑边”，于是某两个人分别在代码里加上了这样一个处理，并分别获得了 \(100pts\) 与 \(35pts\) 的好成绩
怎么会是呢？
考虑 \(wqs\) 二分的过程，我们在凸包上二分直线来计算切点，然后据此移动指针
然而我们会发现可能遇到“三点共线”的相同斜率的情况，或是附加值必须定成小数才能恰好取到 \(x = m\) 的点但同时也会 \(TLE\)
研究博客 + \(max0810\) 不厌其烦的讲解后终于发现我们需要确保用来 \(Dp\) 的每个物品的每个属性都要确定一个偏序关系，而根据这个钦定的偏序关系考虑这会对二分造成选择次数增多还是减少的影响，再来确定移动指针的判断依据是 \(\geq\) 还是 \(\leq\)，这样就可以允许 \(wqs\) 二分有了容错的空间，保证能够取到与 \(x = m\) 情况下最优答案等价的情况
形象化一点说就是在面临“三（切）点共线”的情况时（斜率一样于是计算出的 \(g[x]\) 值也一样，因此不一定要恰好取到 \(x = m\) 也可以计算出 \(x=m\) 时的最优答案），是钦定选取最右侧的点还是最左侧的点，如果钦定顺序与判断条件不一致的话便很有可能取不到最优答案
于是这个困扰机房长达 \(3M\) 的细节终于被解决掉（然后就可以开始改题了）
应用
自己做的第一道有模有样的例题：[IOI2000] 邮局 加强版 加强版
联考遇到的神秘题：Gym 104492I
（还停留在构思阶段，悲）
