2024多校联训游记

Day -1

刚考完月考，还没来得及沉浸在独属于 $OI$ 的文化课悲哀中，下午就赶到机房紧急 $Updating$ 给 $C$ 层同学比赛的题目，在洛谷和 $LemonLime$ 上验 $std$ 验了好几次确定了没锅。结果集训最后一天 $C$ 层同学考我们的题时 $T3$（本人及 $Mortal$_ $Fate$ 负责）所有同学的程序兼 $std$ 全部 $RE$。后来发现是数据的答案文件用了 $.ans$ 而不是 $accoders$ 只支持的 $.out$，还好集训结束后没被拷打表演跳舞、、

Day 0

上午正常上文化课，下午到机房极限调完P2470 [SCOI2007] 压缩跑路去集训学校（成华区好荒凉、、）

第一次尝其他学校的伙食感觉还挺好

第一次为了避免被当地原住民当猴观赏借了原住民的外套尝试混入

第一次住别人拥有电梯和独立浴室的宿舍感慨 CDQZ你是什么#@$

Day 1

第一天早上就打模拟赛（emmm稍微有点不习惯于是状态貌似不是很好）、

$T1$ 显然是一段连续区间的数的乘积，本来想通过质因数分解看看能不能直接找出所有因数（然而显然那时还不知道有 $Pollard -Rho$ 于是果断放弃开始暴力），然后又发现左右端点差距不可能太大，于是想能不能直接找出这个可能的区间。最后看完题解才发现正解其实就根据这种性质对 $n$ 开 $k$ 次根然后判断该数为起点的连续 $k$ 个数相乘能否得到 $n$ 即可。

$T2$ 存在偶数列的情况比较好做，先写了，然后开始考虑对于奇数列的情况，把前 $3$ 列单独提出来处理而后面情况同偶数列，但是考场上并没有推出相应可行的构造方案，最后还在纠结是不是会有 $Dp$ 做法，$TLE$

$T3$ 看过后直接开始暴力模拟，然而时间不够写线段树的暴力分了，寄

$T4$ 知道是 $NOIP2024 T4$ 改编但是有状压在的前提下感觉会调的比较久，没写，寄

最后一共 $48pts$，$Rank:35$

下午是学长 $fsfdgdg$ 的讲课，估计只有李超树和吉司机线段树的部分没练过，其他感觉还好（主要集训开始后下午一般都改题去了，讲课都是偶尔调出腾讯会议界面看一下）抽空写了扫描线的板子

Day 2

~~似乎有点进入状态了（？）~~

$T1$ 以为是折半搜索于是开写，然后发现根本过不去（然而我考虑过在对角线合并贡献）、事实上赛后证明是我傻逼没有考虑同样从两边向中间合并的 $Dp$ 后合并贡献……

$T2$ 只根据题意写了模拟和特殊性质，知道是根据 $nan$ 分析交换的性质（其实只有在开头的特殊情况，后面正常排序就行了），但是没有静心仔细思考拿到分就开始跑路了（可能会想的出来但是就拿不到后面的暴力分了，而且根据我对当时的状态的估计要写出来有点悬、）

$T3$ 本来直接交完全的爆搜有 $44$ 分的，然而我硬是写了个迭代加深要跑满每一层最后混了一个 $15pts$（悲）。当然隔壁大佬 $int08$ 使用含有一定正确性的乱搞做法拿到了 $93pts$ 并在赛后调整待选序列顺序及数据分治操了过去、蚌不住。然后网上还找到纯靠优化拿到 $96pts$ 的爆搜，更蚌不住。

$T4$ 知道是线段树后想都没想直接开始暴力，中途发现锅了开始纠正然后奇迹般的在最后 $10min$ 内调了出来（写数据结构暴力最顺畅的一次）

最后一共 $115pts$，$Rank:26$

下午听大神 $Nityacke$ 讲树分治和 $LCT$ ，然而由于上午的比赛意犹未尽于是果断选择调题（所以讲课内容只能后面去消化了）

林荫的同学终于来了，晚上刚好找到一个排球，于是产生了全体 $CDQZ$ 后续集训期间几乎每日 $1/1$ 的团建项目（事实证明上午和下午有了课间之后去打球是挺放松的）

Day 3

林荫同学 $H$_ $W$_ $Y$ 讲根号数据结构，前半段尽量跟上了思路，后面写题去了于是开始打晃、

虽然下午兼晚自习专注刷题但是也只做了 $4$ 道题（主要是第一天讲课的题目），总感觉平时打题的时候思维频率没有赛时的正常水平高导致效率太低了

Day 4

刷题+字符串专题，大部分学过，主要是题目做法比较新。把模板题打完就听了下大体的思路完事。不敢保证完全理解（主要连续打比赛让人有点倦了），后面的题没怎么练（好像那天在调第二次考试的 $T1$，在几次卡常兼排查后终于过了，原因竟然是 $add, mul$ 等函数调用太多、）

Day 5

图论兼网络流专题，顺便把之前快忘干净的算法捡了起来。学长主要讲的是最大流的建模及最小割的转换，后面补充了一个“模拟网络流”的知识块，这部分应该比较新奇。本来说做点题后学下预流推进式网络流的（虽然对于 $OI$ 可能没什么用），但是直到现在都还没开动、

具体原因是当时正好遇到了一道 $YnOI$此时此刻的光辉，思路确实不怎么难想（~~连我都想出来了~~），但是代码实现稍微有点不好评价（写了 $4k$，然后调了我几乎一整天），提前接触了基于随机数思想的 $Miller-Rabin$ 和 $Pollard-Rho$，后者在讲数学部分的时候由学长（广东黄队）正式介绍

Day 6

放假！！

各回各家暂做休整，外地各校同学被教练带着去城里到处玩（有点羡慕）

Day 7

返回集训后第一场赛，勉强没挂（此时此刻其他同学刚开始放清明假）

$T1$ 在草稿本上写写画画，然后发现把序列里每两项相邻合并后统计 $gcd$ 即可得到所有子段的情况，然后通过跑大数据发现随机数据下这样的合并下只需要大约 $O(\sqrt{n})$ 甚至是 $O(\log{n})$ 次以内便会使整个序列变为 $1$，于是记录两个 $flag$ 判断一下新合并出的 $gcd$ 是否均相同或被统计过，直接 $break$ 即可，于是得到了一个假 $O(n^{2})$ 的算法（有一说一考场上还是觉得挺悬的没想到出题人没有卡这种做法）

$T2$ 一眼组合+ $Dp$，但是最后用 $Dp$ 没有考虑出来，原本思路是保证全 $R$ 能走到后在前面插 $LR$ 随即调换顺序即可，但是后面意识到中间如果有连续极长 $R$ 段可能导致提前到达，于是无力回天……题解通过巧妙构建方格图转换了题意使得题目更容易处理，具体如下：

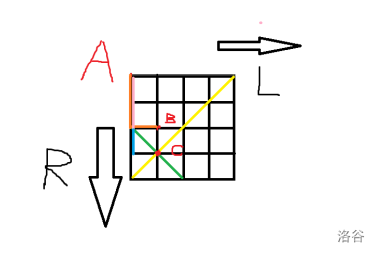
$T3$ $O(n^{4})$ 暴力走人

$T4$ 线段树直接单纯 $pushup$ 维护 $gcd$ 的做法显然假了

然而最后$120pts$，$Rank:17$，还不错

下午调题+写题恢复下手感（好吧本人承认有摆烂嫌疑）

Day 8

开启省选模拟被初中牲完虐的模式、、

$T1$ （不完全型煞笔题）首先显然选球只能够在两端选并且可以先特判总数是否整除每轮选择数，同时红蓝球是否比例相同，不过正解居然只需要用栈直接模拟插入然后判断最末尾的球是否符合条件即可（wssb）

$T2$ （完全型煞笔题）赛场上瞎猜序列全为 $1$ 的特殊性质居然蒙对了，然后考虑选哪种集合满足条件。嗯对然后搜索都写出来了没反应过来就是离 $m$ 刚好差小于一人贡献的人的集合，然后就挂了（wssb * 2）

$T3$ 赛场上只写了暴力跳父亲的暴力，赛后林荫同学表示就是树上分块后的一种典型处理（显然本人当时似乎没有认真听到这段）

总计 $50pts$，$Rank: 25$，考场上几乎一直在写搜索，搜索成功拿下本场 $MVP$

然后讲 $Dp$ 的整个下午都在为自己的煞笔状态买单，晚自习正常写题

Day 9

当天没有考试，于是先把前面网络流建模这种码量小的题写了

$Dp$ 的优化基本上前面讲过（反正我听到的部分是这样的），貌似大家一致认为后面的题会稍微耗时多一点于是果断选择先刷前面遗留的题

或者是一边调前面出现神奇问题的比塞题，并一边奢望着被不知情的讲课学长给占掉的课间休息

或者~~幸灾乐祸地~~了解到其他同学的假期结束了

Day 10

~~省选爆炸记~~，虽然都被队爷 $fsfdgdg$ 称为简单题

$T1$ 学过线性基的人肯定一眼有思路，但是显然我们并没有学过线性基，于是开始写 $Dp$。由于中途觉得 $T2$ 似乎更可写跑去调了接近 $3h$ 的 $T2$ 导致最后 $T1$ 的 $Dp$ 没有调完

$T2$ 在错误理解题意的情况下写了大概 $1.5h$，随后当即更新思路重构代码。然后又一次地没有考虑出 $Dp+$ 容斥的组合，$1.5h$ 后宣布该题报废。不过这只是正解的其一做法，另一种做法充分利用正难则反的思想，直接枚举插入的等差序列的长度并加上前缀和优化到 $O(n^{3})$

$T3$ 最无脑的 $O(n\log^{2}{n})$ 模拟居然也写锅了，感觉一夜回到解放前，寄

最后显然 $0pts$，$Rank:34$。之前 $NOIP$ 模拟的时候最多还有 $50$ 名左右，看来还有直接弃赛的同学啊……

晚上寝室里聊天聊地忘乎所以导致 $00:00$ 后才睡下，幸好第二天没有考试

Day 11

上午正常写题（尤其先把上一天考试遇到的线性基的模板给过了），正准备再写的时候突然想起今天好像要讲多项式，于是先掏出古老的多项式模板继续调当年没过的多项式幂函数（加强版）

然后才发现当年怎么改都死活不过是因为没有发现题目里没有限定 $a_{0}=1$ 这一条，于是多项式 $ln$ 及多项式 $exp$ 的前提不再，需要先强制转化一下同时处理一下新出现的 $0$

下午的课由集训队现役同学倾情呈现，但是只有代数学的部分，没有多项式，理由是多项式属于十级知识点不怎么考、、所以就只能勉强地盯着屏幕上看不懂的数学公式发呆（毕竟这玩意只要开头晃一下后面就不用听了，除非刚好遇到另一个新知识点开讲的情况），谁让没有预习呢……

Day 12

（咕咕咕）

最后一天晚上了，大家在寝室里陪广东老哥聊天聊地痛快，又是一个 $00:00$

Day Last

最后一场比赛~~助我卷铺盖走人~~（字面义）