学习笔记（7）SA（后缀数组）

一、引入

后缀数组中存储字符串 \(S\) 的所有后缀按字典序排序后的结果，主要需要 \(sa, rk\) 两个数组进行求解，具体而言：

\(sa[i]\) 存储字典序第 \(i\) 小的后缀编号（即起始下标）//后缀数组

\(rk[i]\) 存储后缀 \(i\) 的排名 //排名数组

示意图：

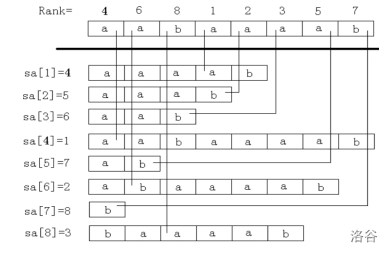
二、倍增法求解

首先应用倍增思想化简规模，这一步是 \(O(logn)\) 的

对于每个后缀，分治地考虑前 \(2^i\) 位参与比较，计算最终排名时通过合并前后长 \(2^{i-1}\) 的子段排名得到。容易发现，这样参与比较的后缀的前缀存在重复的情况，也就是 \(rk[i]\) 会有重复值，这时不妨将 \(rk\) 数组视为衡量字典序相对大小的工具。而由于 \(sa[i]\) 不可重，在合并求解新排名时不妨强制钦定一个顺序（对相对排名的计算不影响）

下面考虑合并前后两段计算新排名的问题

显然这是一个针对 \(<rk1,rk2>\) 的二元组的排序问题，直接调用 \(sort\) 函数是 \(O(nlogn)\) 的，复杂度不够优秀。发现需要排序的 \(rk\) 序列值域在 \([1,n]\)，于是可以考虑用计数排序在 \(O(n)\) 的时间内处理出新的 \(rk\) 序列（同时桶 \(tot\) 的规模可以随枚举的子段长度 \(k\) 及当前的 \(rk_{max}\) (不妨记为 \(sz\)) 逐步递增，可以大大优化常数）

由计数排序的原理可知，桶 \(tot[i]\) 内记录的值相当于表示了序列中该种值的排位范围，为了保证第一，二关键字均有序，可以对第一关键字计数，并按第二关键字倒序枚举赋予排名

然后是如何保证按第二关键字（按大小）倒序的问题。记录 \(sec[i]\) 表示第二关键字排名为 \(i\) 的后缀对应的第一关键字的位置下标，为了补齐 \(2^i\) 长度添加的 \(0\) 字典序是最小的，先存入 \(sec\) 中。然后按上一次合并得到的 \(sa\) 两两配位，合并得到大一倍规模的子串（由于是按先后顺序依次 \(+k\) 顺序地合并，所以一定是原串的子串），实现如下：

int cnt = 0;
for(int i = n - k + 1; i <= n; i++) sec[++cnt] = i;
for(int i = 1; i <= n; i++) if(sa[i] > k) sec[++cnt] = sa[i] - k;

合并过程示意图：

重复上述步骤（处理新的 \(sec\) ->排序，更新 \(sa\) ->更新 \(rk\)）直到 \(sz==n\) 即可，总复杂度 \(O(nlogn)\)

三、应用

目前只学了求解同一字符串两两任意后缀的 \(LCP\)

新定义：\(height[i]\) 表示 \(suf(sa[i])\) 与 \(suf(sa[i-1])\) 的 \(LCP\)，可借此求解任意两个后缀的 \(LCP(x,y)\) (具体证明太菜了就不写了，翻下 \(OIwiki\) 也不是什么麻烦事、)，另通过 \(h[i] (=height[rk[i]])\) 辅助求解：

void get_h(){
	int h = 0;
	for(int i = 1; i <= n; i++){
		if(rk[i] == 1) continue;
		if(h) --h; //重要性质：h[i]>=h[i-1]-1
		int j = sa[rk[i] - 1];
		while(j + h <= n && i + h <= n && s[i + h] == s[j + h]) ++h;
		height[rk[i]] = h;
	}
}

查询时即取 \((x,y]\) 的 \(height[rk[i]]_{min}\) 即可：

int LCP(int x, int y){
	int ans = n;
    if(rk[x] > rk[y]) swap(x, y);
	for(int i = rk[x] + 1; i <= rk[y]; i++) ans = min(ans, height[i]);
	return ans;
}

模板：# P3809 【模板】后缀排序

点击查看代码

#include <bits/stdc++.h>
#define N 1000005
#define S 256
using namespace std;
int n, sz;
char s[N];
int sa[N], rk[N], tot[N], sec[N], rk2[N], height[N];
void get_SA(){
	for(int i = 1; i <= n; i++) ++tot[rk[i] = s[i]];
	for(int i = 1; i <= sz; i++) tot[i] += tot[i - 1];
	for(int i = n; i; i--) sa[tot[rk[i]]--] = i;
	for(int k = 1; k <= n; k <<= 1){
		int cnt = 0;
		for(int i = n - k + 1; i <= n; i++) sec[++cnt] = i;
		for(int i = 1; i <= n; i++) if(sa[i] > k) sec[++cnt] = sa[i] - k;
		memset(tot + 1, 0, sz << 2);
		for(int i = 1; i <= n; i++) ++tot[rk[i]];
		for(int i = 1; i <= sz; i++) tot[i] += tot[i - 1];
		for(int i = n; i; i--) sa[tot[rk[sec[i]]]--] = sec[i];
		sz = 1;
		memcpy(rk2 + 1, rk + 1, n << 2);
		rk[sa[1]] = sz;
		for(int i = 2; i <= n; i++){
			rk[sa[i]] = (rk2[sa[i]] == rk2[sa[i - 1]] && rk2[sa[i] + k] == rk2[sa[i - 1] + k])? sz : ++sz; 
		}
		if(sz == n) break;
	}
}
void get_h(){
	int h = 0;
	for(int i = 1; i <= n; i++) rk[sa[i]] = i;
	for(int i = 1; i <= n; i++){
		if(rk[i] == 1) continue;
		if(h) --h;
		int j = sa[rk[i] - 1];
		while(j + h <= n && i + h <= n && s[i + h] == s[j + h]) ++h;
		height[rk[i]] = h;
	}
}
int LCP(int x, int y){
	int ans = n;
	for(int i = x + 1; i <= y; i++) ans = min(ans, height[i]);
	return ans;
}
int main(){
	scanf("%s", s + 1);
	n = strlen(s + 1);
	sz = S;
	get_SA();
	for(int i = 1; i <= n; i++) printf("%d ", sa[i]);
	return 0;
}