学习笔记(6)分块与莫队
注:两种算法严格来说均属于“优雅的暴力”,故——
该怎么暴力维护时就怎么维护
分块
考虑如下形式的问题:
给定长度为 \(n\) 的序列,\(m\) 次操作,可以是单点修改+区间查询 / 区间修改+单点查,不过数据规模 \(1e5\)
直接暴力做显然是 \(O(1)\) 与 \(O(n^2)\) 的,于是我们考虑稍微平衡一下修改与查询之间的复杂度(其实算是根号分治的思想),将原序列适当划分为多个“块”,对每一个块可以进行预处理,便于查询,块外的朴素暴力,统计答案时分整块部分及散块部分后合统计,这就是分块的基本思想
一般来说,块长需要根据题目需要与代码实现计算最优的块长(依赖基本不等式),不过一般取 \(\sqrt{n}\) 即可,有时候直接钦定块长也是比较可取的
关于复杂度——
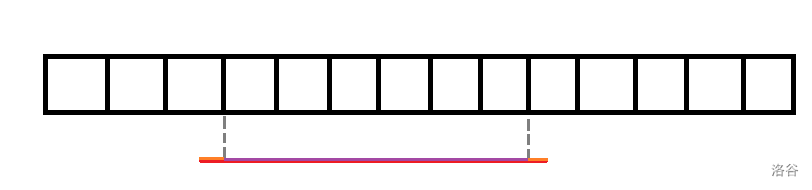
由于块数是 \(O(\sqrt{n})\) 的 ,每块长度也是 \(O(\sqrt{n})\) 的,故若处理单块/单点答案的复杂度为 \(O(k)\),则有 \(O(kn \sqrt{n})\) 的优秀复杂度
模板(?
某人做法:分别对整块区间及块内区间统计答案(整块区间前缀和预处理后 \(O(1)\) 计算,两侧暴力),并存储在桶内,循环时判最大值即可(不满上界的 \(O(n^2)\),\(\approx O(n \sqrt{n})\)),稍微优化了一下处理块间答案的前缀和数组
题解做法:预处理 \(p[l][r]\) 表示块 \(l\) 到块 \(r\) 的众数,根据分析,答案不是整块区间的众数即是两侧块内区间的数,剩下处理相同
某人古早时期代码
#include <bits/stdc++.h>
#define N 50005
using namespace std;
int n,m,x,len,cnt;
int a[N],b[N],id[N],sum[int(sqrt(N))][N];
void init(){
sort(b+1,b+n+1);
cnt=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++){
int now=lower_bound(b+1,b+cnt+1,a[i])-b;
a[i]=now;
}
for(int i=1;i<=id[n];i++){
for(int j=1;j<=cnt;j++) sum[i][j]=sum[i-1][j];
for(int j=(i-1)*len+1;j<=i*len && j<=n;j++) ++sum[i][a[j]];
}
}
int solve(int l,int r){
if(l==r) return a[l];
int res=cnt,now=0;
int lt=id[l];
int rt=id[r];
if(l>(lt-1)*len+1) ++lt;
if(r<rt*len) --rt;
int use[cnt+1];
for(int i=0;i<=cnt;i++) use[i]=0;
for(int i=l;i<min(n,(lt-1)*len+1);i++) ++use[a[i]];
for(int i=rt*len+1;i<=r;i++) ++use[a[i]];
for(int i=1;i<=cnt;i++){
use[i]+=sum[rt][i]-sum[lt-1][i];
if(use[i]>=now){
if(use[i]==now) res=min(res,i);
else res=i;
now=use[i];
}
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
len=sqrt(n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
b[i]=a[i];
id[i]=(i-1)/len+1;
}
init();
for(int i=1;i<=m;i++){
int l,r;
scanf("%d%d",&l,&r);
l=((l+x-1)%n)+1;
r=((r+x-1)%n)+1;
if(l>r) swap(l,r);
x=b[solve(l,r)];
printf("%d\n",x);
}
return 0;
}
应用
有点针对 \(lxl\) 的套题、、
考虑到分块的复杂度是带 \(\sqrt{n}\) 的,于是类似于二分的 \(\log{n}\) 并不能较好的与之适配(指基本上会让复杂度多带上一个 \(\log\),很明显 \(lxl\) 并不会让你就此过掉他的duliu题),所以如果做题时需要强制在线+根号做法的,可以考虑一下分块(貌似目前也只有这个通用的根号算法)
\((Updating \dots)\)
莫队
常规莫队
同样身为解决多次区间操作的算法,却只能离线处理(虽然好像有什么离谱操作可以尝试在某些情况下修改成某种意义上的在线)
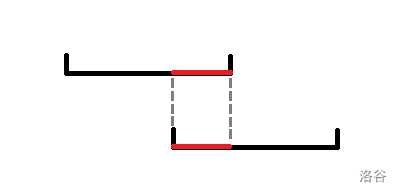
考虑两次查询区间有交集时,中间红色部分的答案会被重复计算(前提是答案满足可加/减性),因此可以设双指针 \(l, r\) 分别表示当前所处的左端点与右端点,将全部查询区间离线,左端点分块后按所在块的编号排序,右端点正常排序(也可以按块编号的奇偶分别升序,降序排序),两个指针移动匹配查询区间,移动时修改贡献,以此“充分利用”重复区间的信息(咋有点“一维”扫描线的感觉)
难点在于处理出答案的可加减性
每个块内跳左端点只有 \(O(\sqrt{n})\) 个,对应的右端点最多跳 \(O(n)\) 次,而一共有 \(O(n)\) 个块,故复杂度为 \(O(n\sqrt{n})\)
\(Tips\):
1、左端点同块的区间,奇数编号其右端点按升序排序,偶数编号其右端点按降序排序
2、部分情况下可以压缩掉 \(if\),省略函数 \((add,del)\) 调用
3、快写快读(一般用莫队的题 \(I/O\) 数据量较大)
4、一般建议先往右跳 \(r\) 再往右跳 \(l\),往左时相反,否则很可能遇到被卡成 \(RE\) 的情况
奇偶排序优化:
bool cmp(Ques x, Ques y){
return (id[x.l] ^ id[y.l])? id[x.l] < id[y.l] : (id[x.l] & 1)? x.r < y.r : x.r > y.r;
}
例题
\(DQUERY - D-query\)
纯模板题
点击查看代码
#include <bits/stdc++.h>
#define N 30000
#define M 1000005
using namespace std;
int n,m,len,tot;
int a[N],id[M],cnt[N],ans[N];
struct query{
int l,r,num;
}q[M];
bool cmp(query x,query y){
return (id[x.l]^id[y.l])? id[x.l]<id[y.l] : (id[x.l]&1)? x.r<y.r : x.r>y.r;
}
int main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%d",&n);
len=sqrt(n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
id[i]=(i-1)/len+1;
}
scanf("%d",&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&q[i].l,&q[i].r);
q[i].num=i;
}
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){
int ql=q[i].l,qr=q[i].r;
while(l<ql) tot-=!--cnt[a[l++]];
while(l>ql) tot+=!cnt[a[--l]]++;
while(r<qr) tot+=!cnt[a[++r]]++;
while(r>qr) tot-=!--cnt[a[r--]]; //减少函数调用以优化常数
ans[q[i].num]=tot;
}
for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
\(XOR - and - Favorite - Number\)
另开一个桶记录能得到相应异或值答案的区间个数
点击查看代码
#include <bits/stdc++.h>
#define N 1000005
#define ll long long
using namespace std;
int n,m,k,len;
ll int sum;
int a[N],id[N];
ll int cnt[N<<1],xo[N<<1],ans[N];
struct query{
int l,r,num;
}q[N];
bool cmp(query x,query y){
return (id[x.l]^id[y.l])? id[x.l]<id[y.l] : (id[x.l]&1)? x.r<y.r : x.r>y.r;
}
void add(int x){
sum+=cnt[xo[x]^k];
++cnt[xo[x]];
}
void del(int x){
--cnt[xo[x]];
sum-=cnt[xo[x]^k];
}
int main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%d%d%d",&n,&m,&k);
len=sqrt(n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
id[i]=(i-1)/len+1;
xo[i]=xo[i-1]^a[i];
}
for(int i=1;i<=m;i++){
scanf("%d%d",&q[i].l,&q[i].r);
q[i].l--;
q[i].num=i;
}
sort(q+1,q+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){
int ql=q[i].l,qr=q[i].r;
while(l<ql) del(l++);
while(l>ql) add(--l);
while(r<qr) add(++r);
while(r>qr) del(r--);
ans[q[i].num]=sum;
}
for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
return 0;
}
带修莫队
虽然莫队本身在被莫队提出时仅限于普通用法(而且据说在提出前曾只在 \(Codeforces\) 的高手圈内小范围流传),不过经过众多 \(OIer\) 与 \(ACMer\) 的努力,莫队被开发出了许多新的进阶形态
由于莫队本身离线且不支持修改,于是在原本的 \(l,r\) 两维基础上加上一维时间 \(t\),将修改与查询操作分开记录,对于查询操作正常做莫队,不过在跳指针过程中,需要再判断当前时间是否在查询区间的“时间”(即修改的个数戳)内,如果相应修改在该范围内则需 \(upd\)
注意带修莫队的块长一般取 \(n^{2/3}\)
例题:
应该是带修莫队的模板题
对于单点修改有一个比较惊艳的实现——\(swap\),时间上的操作甚至可以统一成一个函数
void upd(int x, int t){
if(q1[x].x <= q2[t].x && q2[t].x <= q1[x].y){
del(a[q2[t].x]);
add(q2[t].y);
}
swap(a[q2[t].x], q2[t].y);
}
完整代码
#include <bits/stdc++.h>
#define N 200005
#define M 1000005
using namespace std;
inline int read(){
char ch = getchar(); int x = 0, f = 1;
while(!isdigit(ch)){if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)){x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n, m, len, tot1, tot2, sum;
int a[N], id[N], L[N], R[N], cnt[M], ans[N];
char s[N];
struct Ques{
int num, x, y, ti;
}q1[N], q2[N];
bool cmp(Ques a, Ques b){return (id[a.x] == id[b.x])? (id[a.y] == id[b.y])? a.ti < b.ti : id[a.y] < id[b.y] : id[a.x] < id[b.x];}
void add(int x){sum += !cnt[x]++;}
void del(int x){sum -= !--cnt[x];}
void upd(int x, int t){
if(q1[x].x <= q2[t].x && q2[t].x <= q1[x].y){
del(a[q2[t].x]);
add(q2[t].y);
}
swap(a[q2[t].x], q2[t].y);
}
int main(){
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
n = read(), m = read();
len = 5055;
memset(L, 0x7f, sizeof L);
for(int i = 1; i <= n; i++){
a[i] = read(), id[i] = (i - 1) / len + 1;
L[id[i]] = min(L[id[i]], i), R[id[i]] = max(R[id[i]], i);
}
// for(int i = 1; i <= n; i++) cerr<<id[i]<<": "; cerr<<endl;
for(int i = 1; i <= m; i++){
scanf(" %s", s + 1);
if(s[1] == 'Q') ++tot1, q1[tot1].num = tot1, q1[tot1].x = read(), q1[tot1].y = read(), q1[tot1].ti = tot2;
else ++tot2, q2[tot2].x = read(), q2[tot2].y = read();
}
sort(q1 + 1, q1 + tot1 + 1, cmp);
int l = 1, r = 0, t = 0;
for(int i = 1; i <= tot1; i++){
int ql = q1[i].x, qr = q1[i].y, qt = q1[i].ti;
while(r < qr) add(a[++r]);
while(l < ql) del(a[l++]);
while(l > ql) add(a[--l]);
while(r > qr) del(a[r--]);
while(t < qt) upd(i, ++t);
while(t > qt) upd(i, t--);
ans[q1[i].num] = sum;
}
for(int i = 1; i <= tot1; i++) printf("%d\n", ans[i]);
return 0;
}
回滚莫队
然而总有一些题目不能完全支持莫队的“加减”修改,例如 \(mex\) 与位置相关的权值维护
不过好在这类题目至少满足“只能加不能减”或是“只能减不能加”的要求
我们舍弃奇偶排序的优化,将右端点严格单调排序(具体是单增还是单减根据只能加还是减确定,加的话就是单增,后文以实现加法为例),询问区间的左端点仍然按照块的编号单增排序
这时我们发现,由于右端点单增,于是对任意块内的区间跳右端点时只会有“加”的操作,于是我们只需要考虑左端点如何“还原”
每次对于一个新块内的左端点,我们将左指针 \(l\) 置为 \(R[i] + 1\),即该块的最右端,于是无论如何跳指针都是向左跳,对每个区间来说便只会有“加”操作了
为了能够继续跳指针,每次跳完右指针后记录当前的答案,便于将该区间“还原”。答案里的贡献于是被直接还原,剩下用以维护的数组等正常执行“减”操作消掉贡献即可。于是所有的操作都在扩充区间,避免了收缩区间的麻烦(回跳只是还原初始状态)
另外实现上,对于左右端点同在一块内的情况我们直接暴力统计
由于每块内,右端点单增,跳右指针最坏是 \(O(n)\) 的,一共 \(O(\sqrt{n})\) 个块;块内所有左端点移动时间复杂度是 \(O(\sqrt{n})\) 的,而一共有 \(O(n)\) 个左端点;同时,暴力统计是 \(O(\sqrt{n})\) 的,所以复杂度是 \(O(n\sqrt{n})\) 的
例题
点击查看代码
#include <bits/stdc++.h>
#define N 100005
#define ll long long
using namespace std;
inline int read(){
char ch = getchar(); int x = 0, f = 1;
while(!isdigit(ch)){if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)){x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n, m, len, tot;
ll mx;
int a[N], b[N], id[N], L[N], R[N], cnt[N], cnt2[N];
ll ans[N];
struct Ques{
int num, l, r;
}q[N];
bool cmp(Ques a, Ques b){return (id[a.l] == id[b.l])? a.r < b.r : id[a.l] < id[b.l];}
void add(int x){
++cnt[x];
mx = max(mx, 1ll * b[x] * cnt[x]);
}
void del(int x){--cnt[x];}
ll force(int l, int r){
ll res = 0;
for(int i = l; i <= r; i++) ++cnt2[a[i]];
for(int i = l; i <= r; i++) res = max(res, 1ll * b[a[i]] * cnt2[a[i]]);
for(int i = l; i <= r; i++) --cnt2[a[i]];
return res;
}
int main(){
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
n = read(), m = read();
len = sqrt(n);
memset(L, 0x7f, sizeof L);
for(int i = 1; i <= n; i++){
a[i] = read(), b[i] = a[i], id[i] = (i - 1) / len + 1;
L[id[i]] = min(L[id[i]], i), R[id[i]] = max(R[id[i]], i);
}
sort(b + 1, b + n + 1);
tot = unique(b + 1, b + n + 1) - b - 1;
for(int i = 1; i <= n; i++) a[i] = lower_bound(b + 1, b + tot + 1, a[i]) - b;
for(int i = 1; i <= m; i++) q[i].l = read(), q[i].r = read(), q[i].num = i;
sort(q + 1, q + m + 1, cmp);
int l = 1, r = 0, p = 1;
for(int i = 1; i <= id[n]; i++){
memset(cnt, 0, sizeof cnt);
l = R[i] + 1, r = R[i];
mx = 0;
for(; id[q[p].l] == i; p++){
if(id[q[p].l] == id[q[p].r]){ans[q[p].num] = force(q[p].l, q[p].r); continue;}
while(r < q[p].r) add(a[++r]);
ll cur = mx;
while(l > q[p].l) add(a[--l]);
ans[q[p].num] = mx;
while(l < R[i] + 1) del(a[l++]);
mx = cur;
}
}
for(int i = 1; i <= m; i++) printf("%lld\n", ans[i]);
return 0;
}
维护 \(mex\),只能减,\(l\) 设为 \(L[i]\),\(r\) 设为 \(n\),剩下的合理依题意修改
点击查看代码
#include <bits/stdc++.h>
#define N 200005
using namespace std;
inline int read(){
char ch = getchar(); int x = 0, f = 1;
while(!isdigit(ch)){if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)){x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
int n, m, len, mx, mex, rx0;
int a[N], id[N], L[N], R[N], cnt[N], cnt2[N], ans[N];
struct Ques{
int num, l, r;
}q[N];
bool cmp(Ques a, Ques b){return (id[a.l] == id[b.l])? a.r > b.r : id[a.l] < id[b.l];}
void add(int x){++cnt[x];}
void del(int x){
--cnt[x];
if(!cnt[x]) mex = min(mex, x);
}
int force(int l, int r){
int res = mx + 1;
for(int i = 0; i <= mx + 1; i++) cnt2[i] = 0;
for(int i = l; i <= r; i++) ++cnt2[a[i]];
for(int i = 0; i <= mx + 1; i++) if(!cnt2[i]){res = i; break;}
return res;
}
int main(){
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
n = read(), m = read();
len = sqrt(n);
memset(L, 0x7f, sizeof L);
for(int i = 1; i <= n; i++){
a[i] = read(), id[i] = (i - 1) / len + 1;
++cnt[a[i]];
mx = max(mx, a[i]);
L[id[i]] = min(L[id[i]], i), R[id[i]] = max(R[id[i]], i);
}
L[id[n] + 1] = 0;
for(int i = 0; i <= mx + 1; i++) if(!cnt[i]){rx0 = i; break;}
for(int i = 1; i <= m; i++) q[i].l = read(), q[i].r = read(), q[i].num = i;
sort(q + 1, q + m + 1, cmp);
int l = 1, r = 0, p = 1;
for(int i = 1; i <= id[n]; i++){
l = L[i], r = n;
mex = rx0;
for(; id[q[p].l] == i; p++){
if(id[q[p].l] == id[q[p].r]){ans[q[p].num] = force(q[p].l, q[p].r); continue;}
while(r > q[p].r) del(a[r--]);
int cur = mex;
while(l < q[p].l) del(a[l++]);
ans[q[p].num] = mex;
while(l > L[i]) add(a[--l]);
mex = cur;
}
while(r < n) add(a[++r]);
while(l < L[i + 1]){
--cnt[a[l]];
if(!cnt[a[l]]) rx0 = min(rx0, a[l]);
++l;
}
}
for(int i = 1; i <= m; i++) printf("%d\n", ans[i]);
return 0;
}


