OI队测题解：

Test 17

 

T1：

 

题目大意：

喵星系有n个星球，标号为1到n，星球以及星球间的航线形成一棵树。

所有星球间的双向航线的长度都为1。小昕要在若干个星球建矿石仓库，设立每个仓库的费用为K。对于未设立矿石仓库的星球，设其到一个仓库的距离为i，则将矿石运回的费用为Di。

请你帮它决策最小化费用。n<=200

 

题解：开始的时候第一眼DP，可是不知道设状态，后来感觉是网络流，但是发现对于仓库哪里无法限流，于是在纠结很久的情况下

　　　想到正解：Tree DP

　　　设一个状态F(x,y)代表第x个点，在y处有个未建仓库，于是对于一个点U和它的子节点V我们可以这样转移：

　　　枚举1--n中的F[V][I]+k的最小值存为Mn，在一次枚举1--n如果F[V][i]>=Mn 那么F(U,i)+=Mn else F(U,i)+=F(V,i)

　　　因为如果F(V,i)>=Mn的话我们完完全全可以新建一个节点，可是这样为什么能保证一个节点新建的费用只算了一次？

　　　那是因为对于建一个仓库它会更优，那么到达它的将是一段连续的点对，那么因为F(U,i)+=F(V,i)，这些点对先会被统计于一个节点

　　　再由这个节点被转移+K，于是保证答案正确性！

 

---

 

T2

 

题目大意：

小奕和小晟正准备下个周末的Party。为这个Party,他们刚刚买了一个非常大的圆桌。他们想邀请每个人，但他们现在不知道如何分配座次。小奕说当有超过K个女孩座位相邻（即这些女孩的座位是连续的，中间没有男孩）的话，她们就会说一整晚的话而不和其他人聊天。 小晟没有其他选择，只有同意她。然而，作为一名数学家，他很快地痴迷于所有可能方案。 题目说明： N个人围绕着圆桌坐着，其中一些是男孩，另一些是女孩。你的任务是找出所有合法的方案数，使得不超过K个女孩座位是连续的。 循环同构会被认为是同一种方案。

 

题解：https://files.cnblogs.com/files/HQHQ/%E8%A7%A3%E9%A2%98%E6%8A%A5%E5%91%8A_ipsc2008_largeparty.pdf

 

神犇题解：http://www.cnblogs.com/DUXT/p/5958205.html

---

 

 

T3

题目大意：

下水道的主干路由n个节点和n-l条边组成，每条边有一个通过它所需的时间Ti。换言之，这是一棵n个节点的带权

树。现在，要用最快的速度赶往目标节点k。下水道有一些塌陷，这导致主干路的某一段路径可以通过该塌陷到另

一条路径。对于一个塌陷，我们用(L1，ri，L2，R2，c)来描述，即对于主干路上L1到R1路径上的任意节点x，L2到

r2路径上的任意节点y，都可以在c的时间内从x走到y。因为不知道自己所在的到底是哪个节点，所以要求出每个节

点到目标节点K的最短距离。注意边是单向的

 

 

题解：

　　1.对于前20分，m、n<=1000 

　　　我们如果暴力建图+spfa是可以（慢慢水过）的，于是我们我们考虑一下建一个中转点K，对于两段要联接S1，S2我们

　　　可以先将S1中的点向K连边权为0的边，在由K向S2连边权为C的边，这样点数与边数就被缩小为O（n）级别。

　　2.考虑另外20分，一条链我们怎么作？

　　　一条链+区间操作显然可以想到线段树这类区间维护结构，于是我们可以利用线段树上的log个点进行区间连边操作

　　　于是问题得到解决！

　　3.一颗树怎么办？树和链是没有区别的，因为我们有树链剖分，直接剖分即可，我们可以建两颗线段树，一个由底层向上

　　　依次连边，一个由上到下依次连边，于是我们只要在两颗线段树中进行区间连边（如操作1）操作！

Test 18

t1:

赛艇游戏 (exciting.cpp/c/pas)
【问题描述】 陶陶参加了学校举行的遥控赛艇比赛。 出于公平的原则，所有比赛用的遥控赛艇统一由举办方提供。 一共有n名选手参加，每名选手共参加m场比赛。

比赛开始前，每名选手都 会由抽签得到m艘遥控赛艇，每艘赛艇都有一个速度值v，每艘赛艇只能参加一
次比赛，参赛顺序由选手自行选择。一场比赛胜出，当且仅当该名选手控制的赛
艇的速度值大于其他所有选手参加该场比赛赛艇的速度值。（其他情况不产生胜 者）
现在陶陶知道了所有选手赛艇的情况，他想知道，每一个人最多可能的获胜 场次和最少可能的获胜场次。

 

题解：

　　官方sol：田忌赛马扩展版（贪心）

　　个人sol:实际上这是我以前写的一道题的二维扩展版我们考虑将所有的从小到大排序，每一个人设一个指针b[j]，

　　　　　　while(a[x][i]>a[j][b[j]]) b[j]++,sum[j]++;

　　　　　　然后扫一遍看是否sum[j]都>0，是的话Ans++，sum[j]--; 最小的同理稍微改一下即可

t2:

【问题描述】 

今天是陶陶的生日，陶陶收到了许多的生日礼物。 在所有礼物中，最与众不同的是一个造型独特的电子钟。

通过阅读说明书后，陶陶发现，这个钟分别有两块显示屏，每个显示屏分别 有一些数位。

特别之处是每个数位只能显示0到6的整数。（即显示7进制意义 下的整数）

善于思考的陶陶想到了一个有趣的问题：如果让两个显示屏分别表示十进制 下 0～n-1 和 0～m-1 的整数（假设第一个屏幕此时表示 i，第二个屏幕此时表示 j），

有多少个整数对(i,j)对应的电子钟的显示状态没有一个数位是重复的呢？

由于电子钟的数位数量是可控的，陶陶在一开始会分别在两个屏幕上一次性 启用最少能够表示n-1及m-1的数位。

在启用一定数位后，若该数字的7进制位 数小于启用的数位位数，则多余位置会显示数位 0。（显示数字 0 至少需要一个 数位） 

 

题解：以为抽屉原理n+m<=7才有解于是暴力dfs模拟即可

 

t3

 

题解：考虑m为质数，直接上inv（乘法逆元）+快速幂即可

　　　考虑m非质数我们则先将m质因子拆分，考虑1--n中每一个数Ai都将m的质因子删去后为ai

　　　于是将ai作为子序列作情况一即可，然而质因子则可以暴力计算即可

 

测试总结：考试过程中时间分配不均，不够自信不相信自己算法，样例没过就放弃（例如t1只是少了一个初始化）

　　　　　写题之前一定要想好代码框架争取一遍A！写代码要细心！

 

Test 19

 

1、一道防 AK 好题
【题目描述】 给定正整数 n 和正整数数组 (1<=i<=n)，现有 n 堆石子排成一列，第 i 堆石子有 个，

其中 对于任一正整数 i(i<n)，第 i 堆石子与第 i+1 堆石子相邻。每次将两堆石子合并成一堆，

新堆 的石子数是原来两堆石子数之和，代价是原来两堆石子数之积，

求合并 n-1 次将 n 堆石子合 并成一堆的代价和最小是多少。 

 

题解：可以证明无论怎么合并代价一定，long long 开不下要用 ull!

 

2、A + B Problem
【题目描述】 给定正整数 n,p 和非负整数 a,b，求

 

，例如当 n=1 时，该结果等于 a+b。由于答案可能很大，请对 p 取模。 

 题解：算法一:p为质数直接求出通项公式（这是一个等比数列）然后快速幂+乘法逆元

　　　 算法二：p为非质数，我们可以用中国剩余定理解决

　　　　　　　但是有更优的写法：我们发现一个问题可以拆成子问题

　　　　　　　例如：n=5的时候可以化为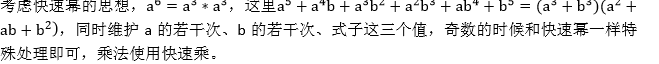

　　　　　　　于是问题解决

3、

题解：我们考虑对于一个变量A，设它的下界为B，上界为C，所以B<=A<=C

　　　所以我们可以知道一些变量之间的关系，于是我们考虑假定知道每个循环变量的值，

　　　对于一个固定的大小关系，我们将大小相同的分为一组，共K组，

　　　于是我们可以知道答案即为C（n，k）

　　　我只要求出某种大小关系有多少种况，于是我们状压DP即可

 

Test 20

1.

题解：我们发现如果第i项为x，那么前i-1项势必出现了1-x-1所以我们考虑设一个这样的状态方程f[i][j]代表

　　　前i个最大的为j的方案数，我们统计答案则为：ans=ans+（a[i]-1)*f[i][max(prea,a[i]]

　　　为了方便我们将求f倒过来即可

2.

 

 

 

题解：我们考虑这些区间如果不重叠方案数即为2^集合个数，如果重叠答案就会变吗？不一定

　　　只有一个区间可以由几个小区间合并而成才可以删除，因为这个区间所能于其他区间形成

　　　的不同的区间，都可以由这几个小区间代替完成，于是可以删除，可以利用并查集来完成这个过程！

3.

题解：还没写完 待更！