Bzoj1479: [Nerrc1997]Puncher打孔机

1479: [Nerrc1997]Puncher打孔机

Time Limit: 5 Sec  Memory Limit: 64 MB
Submit: 22  Solved: 14
[Submit][Status][Discuss]

Description

打孔机是一种在票上打孔的装置， 假设票是一个M*N的矩阵，矩阵行列间距相等，你可以选择在M*N个位置上打穿或不打穿，这样就有 2^(M*N)-1（至少要打一个孔）不同的方案数。 但是我们的问题并不是这么简单的，如果两种方案经过如下的若干操作后，打穿的孔刚好重合，那么认为这两个方案是相同的： •翻转 •旋转0，90，180，270 •平行移动 显然如果两种方案上孔的数目不同，那么必然是不同的方案。现在你的问题就是给定M，N，算出所有不同的方案数。

Input

文件包含两个数M(≤6), N (≤10) ,用空格分开。

Output

只有一行，为所求的方案数。

Sample Input

3 3

Sample Output

85

HINT

---

题解：

　　看到这道题，没有一点思路，看了题解才知道什么叫做恶心数学题【此处D膜拜出题人】

　　我们考虑忽略平移对这道题目的影响，毕竟我们对于旋转翻转之类的比较了解，于是我们思考设立一个状态状态来包含所有置换

　　•于是我们设：

　　　　F_u-v表示u行v列的矩阵中，在其每条边上都至少有一个格子被染色，其本质不同的染色方案数。

　　　　因为每条边上都有染色的格子，所以无论向哪个方向平移，都会有染色的格子移出矩阵，所以无法进行平移操作的，那么只需要考虑翻转和旋转了。

　　•

　　　　G0_uv　   表示每条边上都至少有一个格子被染色的u行v列的矩阵，总的染色方案数。

　　　　G¹_uv　　表示每条边上都至少有一个格子被染色的u行v列的矩阵，其通过旋转180度保持不变的染色方案数。

　　　　G2_uv　　表示每条边上都至少有一个格子被染色的u行u列的矩阵，其通过旋转90度或270度保持不变的染色方案数。

　　　　G3_uv　　表示每条边上都至少有一个格子被染色的u行v列的矩阵，其通过上下翻转保持不变的染色方案数。

　　　　G4_uv　　表示每条边上都至少有一个格子被染色的u行v列的矩阵，其通过左右翻转保持不变的染色方案数。

　　　　G5_uv　　表示每条边上都至少有一个格子被染色的u行u列的矩阵，其通过沿某条对角线翻转保持不变的染色方案数。

　　　　求得所有的G值，F值就只需套用引理即可。而的求法也都大同小异。

　　•　求法：容斥原理！！！

　　　　就是应用容斥原理，将所有格子任意染色，减去第一行或者第u行或者第一列或者第v列没染色，再加上第1行和第u行均未染色……即：

　　　　

　　　　

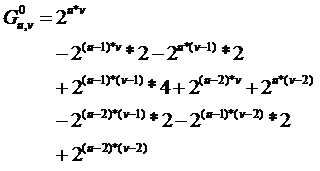
　　　　旋转180度不变，实际上就是前个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

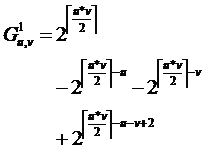
　　　　旋转90度或者270度，则是由左上角的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

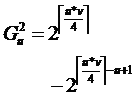
　　　　上下翻转，则是由上半部分的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

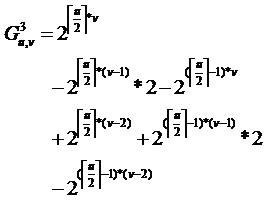
　　　　左右翻转，则是由半边部分的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

　　　　

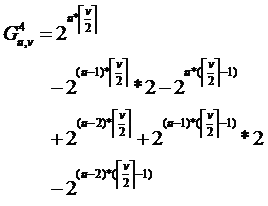
　　　　沿对角线翻转，则是由对角线上面部分的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

 　　　　

　　　　

 

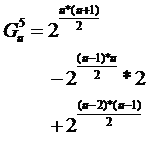
　　　　完美解决！！！

　　　　参考文献： 《Puncher》解题报告

---

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#define ll long long 
using namespace std;
ll ans;
int n,m;
int read()
{
    int x=0,f=1; char ch;
    while (ch=getchar(),ch<'0'||ch>'9') if (ch=='-') f=-1;
    while (x=x*10+ch-'0',ch=getchar(),ch>='0'&&ch<='9');
    return x*f;
}
ll ksm(ll x,int k)
{
    ll res=1;
    for (int i=k; i; i>>=1,x*=x) if (i&1) res*=x;
    return res;
}
ll get0(int u,int v)
{
    ll res=0;
    res=ksm(2,u*v)
        -ksm(2,(u-1)*v)*2-ksm(2,u*(v-1))*2
        +ksm(2,(u-1)*(v-1))*4+ksm(2,(u-2)*v)+ksm(2,u*(v-2))
        -ksm(2,(u-2)*(v-1))*2-ksm(2,(u-1)*(v-2))*2
        +ksm(2,(u-2)*(v-2));
    return res;
}
ll get1(int u,int v)
{
    ll res=0;
    res=ksm(2,ceil(u*v/2.0))
        -ksm(2,ceil(u*v/2.0)-u)-ksm(2,ceil(u*v/2.0)-v)
        +ksm(2,ceil(u*v/2.0)-u-v+2);
    return res;
}
ll get2(int u,int v)
{
    ll res=0;
    res=ksm(2,ceil(u*v/4.0))-ksm(2,(ceil(u*v/4.0)-u+1));
    return res;
}
ll get3(int u,int v)
{
    ll res=0;
    res=ksm(2,ceil(u/2.0)*v)
        -ksm(2,ceil(u/2.0)*(v-1))*2-ksm(2,(ceil(u/2.0)-1)*v)
        +ksm(2,ceil(u/2.0)*(v-2))+ksm(2,(ceil(u/2.0)-1)*(v-1))*2
        -ksm(2,(ceil(u/2.0)-1)*(v-2));
    return res;
}
ll get4(int u,int v)
{
    ll res=0;
    res=ksm(2,u*ceil(v/2.0))
        -ksm(2,(u-1)*ceil(v/2.0))*2-ksm(2,u*(ceil(v/2.0)-1))
        +ksm(2,(u-2)*ceil(v/2.0))+ksm(2,(u-1)*(ceil(v/2.0)-1))*2
        -ksm(2,(u-2)*(ceil(v/2.0)-1));
    return res;
}
ll get5(int u,int v)
{
    ll res=0;
    res=ksm(2,u*(u+1)/2.0)-ksm(2,(u-1)*u/2.0)*2+ksm(2,(u-2)*(u-1)/2.0);
    return res;
}
ll get(int u,int v)
{
    ll res=0;
    if (v==1)
    {
        if (u==1) return 1;
        return (ksm(2,u-2)+ksm(2,(u+1)/2.0-1))/2.0;
    }
    else
    {
        if (u==v)
        {
            res=(get0(u,v)+get1(u,v)+2*get2(u,v)+get3(u,v)+get4(u,v)+2*get5(u,v));
            return res/8;
        }
        else if (u>v)
        {
            res=(get0(u,v)+get1(u,v)+get3(u,v)+get4(u,v));
            return res/4;
        }
    }
}
int main()
{
    n=read(); m=read();
    for (int u=1; u<=max(n,m); u++)
        for (int v=1; v<=min(u,min(n,m)); v++)
        ans+=get(u,v);
    printf("%lld\n",ans);
    return 0; 
}