【1906】算法设计与分析学习笔记——复杂度分析

一、典型插入排序复杂度

template<class Type>
void insertion_sort(Type *a, intn)
{
  Type key; // cost times 
  for (inti= 1; i< n; i++){                  // c1   n
          key=a[i];                          // c2   n-1
          intj=i-1;                          // c3   n-1
          while( j>=0 && a[j]>key ){         // c4   sum of ti
          a[j+1]=a[j];                       // c5   sum of (ti-1)
          j--;                               // c6   sum of (ti-1)
      }
     a[j+1]=key;                             // c7    n-1
     }
}

 

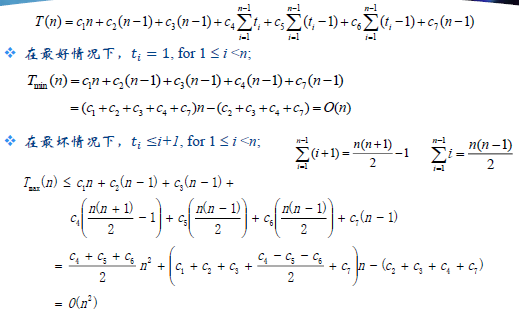
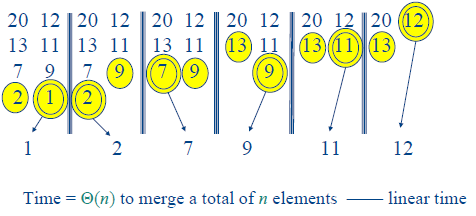
 归并排序：

二、复杂度分析方法

计算递推式通常有三种方法：代入法、迭代方法（iterating）和主方法（master method）。

 1、代入法

 

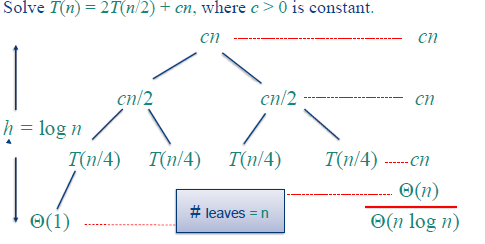
2、递归树

 

 

 

 

3、主定理方法

主方法 主定理：设a≥1a≥1a≥1和b>1b>1b>1为常数，f(n)f(n)f(n)是一个函数，T(n)T(n)T(n)由下面的递推式定义： 

                                       T(n)=aT(n/b)+f(n)

 

 

 

 

三、摊还分析

摊还分析(Amortized analysis)

• 求取数据结构的一个操作序列中所执行的所有操作的平均时间，来评价操作的代价
• 不同于平均情况分析，它并不涉及概率，可以保证最坏情况下每个操作的平均性能
• 即使操作序列中某个单一操作的代价很高，但其平均代价可能是很低的

基本方法

• 聚合分析(aggregate analysis)
• 核算法(accounting method)
• 势能法(potential method)

动态给数据分配空间，提高空间利用率！