【1904】数据结构学习笔记——基础知识

一、问题解决思路

编写程序解决问题的思路：

        1、将问题抽象成数学模型（用数据进行问题的描述）；

        2、分写问题的数据量的大小和数据之间的关系；

        3、数据的存储和表现的实现方式（用什么变量描述，数组，指针，vector）和定义方式（double、int 、float）

        4、考虑数据处理时需要完成的运算（如何将函数抽象成一个函数进行实现！）

        5、编写对应的程序；

        6、Debug—>优化；

二、引言说明

• 一般常见的数据结构：线性关系、树形结构、网状结构。（实例：图书检索，档案资料自动化、交通灯管理etc）
• 基本定义：数据，数据元素，数据项（最基本的数据单位）、数据对象（有限/无限）
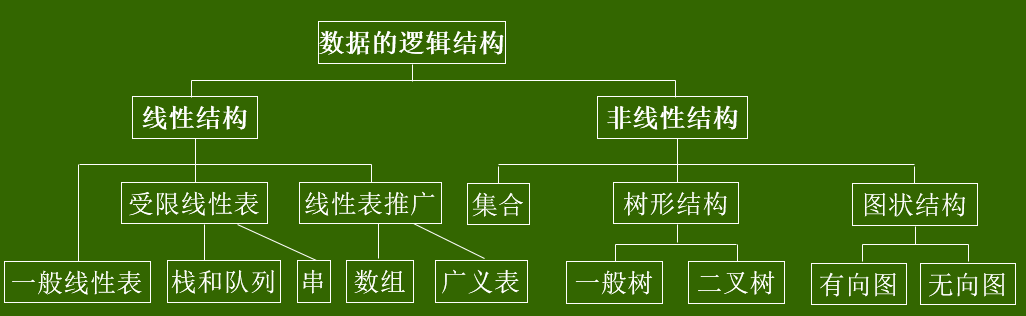
• 数据结构：数据元素之间的关系；逻辑结构：元素之间的关系；典型：集合、线性、树形、图状；
• Data-Structure=(D,S)
• 典型的两种存储结构：顺序存储（存放地址连续）和链式存储（存在指针，指针表示元素之间的逻辑关系）；
• 存储结构的分类：
• 线性结构：结构中的数据元素之间是存在一对一的关系的；
• 

   

• 抽象数据类型（ADT）：ADT=(D,S,P)——D是数据对象，S是D上的关系集，P是对D的基本操作集。

• 算法和程序是两个不同的概念。一个计算机程序是对一个算法使用某种程序设计语言的具体实现。算法必须可终止意味着不是所有的计算机程序都是算法。

• 算法中基本操作重复执行的次数是问题规模n的某个函数，其时间量度记作 T(n)=O(f(n))，称作算法的渐近时间复杂度(Asymptotic Time complexity)，简称时间复杂度。

• 六种计算算法时间的多项式是最常用的。其关系为：

  O(1)<O(㏒n)<O(n)<O(n㏒n)<O(n2)<O(n3)
  指数时间的关系为：
  O(2^n)<O(n!)<O(n^n)

• 空间复杂度(Space complexity) ：是指算法编写成程序后，在计算机中运行时所需存储空间大小的度量。记作： S(n)=O(n)) 其中： n为问题的规模(或大小)。——一维数组a[n]： 空间复杂度 O(n)；二维数组a[n][m]： 空间复杂度 O(n*m)