PyTorch 中的乘法:mul()、multiply()、matmul()、mm()、mv()、dot()
torch.mul()
函数功能:逐个对 input 和 other 中对应的元素相乘。
本操作支持广播,因此 input 和 other 均可以是张量或者数字。
举例如下:
>>> import torch
>>> a = torch.randn(3)
>>> a
tensor([-1.7095, 1.7837, 1.1865])
>>> b = 2
>>> torch.mul(a, b)
tensor([-3.4190, 3.5675, 2.3730]) # 这里将 other 扩展成了 input 的形状
>>> a = 3
>>> b = torch.randn(3, 1)
>>> b
tensor([[-0.7705],
[ 1.1177],
[ 1.2447]])
>>> torch.mul(a, b)
tensor([[-2.3116],
[ 3.3530],
[ 3.7341]]) # 这里将 input 扩展成了 other 的形状
>>> a = torch.tensor([[2], [3]])
>>> a
tensor([[2],
[3]]) # a 是 2×1 的张量
>>> b = torch.tensor([-1, 2, 1])
>>> b
tensor([-1, 2, 1]) # b 是 1×3 的张量
>>> torch.mul(a, b)
tensor([[-2, 4, 2],
[-3, 6, 3]])
这个例子中,input 和 output 的形状都不是公共形状,因此两个都需要广播,都变成 2×3 的形状,然后再逐个元素相乘。
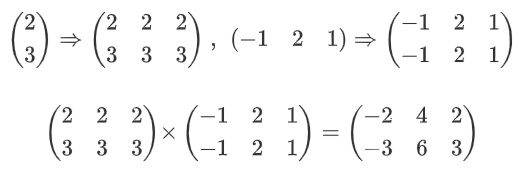
由上述例子可以看出,这种乘法是逐个对应元素相乘,因此 input 和 output 的前后顺序并不影响结果,即 torch.mul(a, b) =torch.mul(b, a) 。
torch.multiply()
torch.mul() 的别称。
torch.dot()
函数功能:计算 input 和 output 的点乘,此函数要求 input 和 output 都必须是一维的张量(其 shape 属性中只有一个值)!并且要求两者元素个数相同!
举例如下:
>>> torch.dot(torch.tensor([2, 3]), torch.tensor([2, 1]))
tensor(7)
>>> torch.dot(torch.tensor([2, 3]), torch.tensor([2, 1, 1])) # 要求两者元素个数相同
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
RuntimeError: inconsistent tensor size, expected tensor [2] and src [3] to have the same number of elements, but got 2 and 3 elements respectively
torch.mm()
函数功能:实现线性代数中的矩阵乘法(matrix multiplication):(n×m) × (m×p) = (n×p) 。
本函数不允许广播!
举例如下:
>>> mat1 = torch.randn(2, 3)
>>> mat2 = torch.randn(3, 2)
>>> torch.mm(mat1, mat2)
tensor([[-1.1846, -1.8327],
[ 0.8820, 0.0312]])
torch.mv()
函数功能:实现矩阵和向量(matrix × vector)的乘法,要求 input 的形状为 n×m,output 为 torch.Size([m])的一维 tensor。
举例如下:
>>> mat = torch.tensor([[1, 2, 3], [4, 5, 6]])
>>> mat
tensor([[1, 2, 3],
[4, 5, 6]])
>>> vec = torch.tensor([-1, 1, 2])
>>> vec
tensor([-1, 1, 2])
>>> mat.shape
torch.Size([2, 3])
>>> vec.shape
torch.Size([3])
>>> torch.mv(mat, vec)
tensor([ 7, 13])
注意,此函数要求第二个参数是一维 tensor,也即其 ndim 属性值为 1。这里我们要区分清楚张量的 shape 属性和 ndim 属性,前者表示张量的形状,后者表示张量的维度。(线性代数中二维矩阵的维度 m×n 通常理解为这里的形状)
对于 shape 值为 torch.Size([n]) 和 torch.Size(1, n) 的张量,前者的 ndim=1 ,后者的 ndim=2 ,因此前者是可视为线代中的向量,后者可视为线代中的矩阵。
对于 shape 值为 torch.Size([1, n]) 和 torch.Size([n, 1]) 的张量,它们同样在 Pytorch 中被视为矩阵。例如:
>>> column = torch.tensor([[1], [2]])
>>> row = torch.tensor([3, 4])
>>> column.shape
torch.Size([2, 1]) # 矩阵
>>> row.shape
torch.Size([2]) # 一维张量
>>> matrix = torch.randn(1, 3)
>>> matrix.shape
torch.Size([1, 3]) # 矩阵
对于张量(以及线代中的向量和矩阵)的理解可看这篇博文。
torch.bmm()
函数功能:实现批量的矩阵乘法。
本函数要求 input 和 output 的 ndim 均为 3,且前者形状为 b×n×m,后者形状为 b×m×p 。可以理解为 input 中包含 b 个形状为 n×m 的矩阵, output 中包含 b 个形状为 m×p 的矩阵,然后第一个 n×m 的矩阵 × 第一个 m×p 的矩阵得到第一个 n×p 的矩阵,第二个……,第 b 个……因此最终得到 b 个形状为 n×p 的矩阵,即最终结果是一个三维张量,形状为 b×n×p 。
举例如下:
>>> batch_matrix_1 = torch.tensor([ [[1, 2], [3, 4], [5, 6]] , [[-1, -2], [-3, -4], [-5, -6]] ])
>>> batch_matrix_1
tensor([[[ 1, 2],
[ 3, 4],
[ 5, 6]],
[[-1, -2],
[-3, -4],
[-5, -6]]])
>>> batch_matrix_1.shape
torch.Size([2, 3, 2])
>>> batch_matrix_2 = torch.tensor([ [[1, 2], [3, 4]], [[1, 2], [3, 4]] ])
>>> bat
batch_matrix_1 batch_matrix_2
>>> batch_matrix_2
tensor([[[1, 2],
[3, 4]],
[[1, 2],
[3, 4]]])
>>> batch_matrix_2.shape
torch.Size([2, 2, 2])
>>> torch.bmm(batch_matrix_1, batch_matrix_2)
tensor([[[ 7, 10],
[ 15, 22],
[ 23, 34]],
[[ -7, -10],
[-15, -22],
[-23, -34]]])
torch.matmul()
torch.matmul() 可以用于 PyTorch 中绝大多数的乘法,在不同的情形下,它与上述各个乘法函数起着相同的作用,具体请看这篇博文



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人