康拓展开及逆康拓展开
概念:
康托展开是一个全排列到一个自然数的双射,常用于构建哈希表时的空间压缩。 康托展开的实质是计算当前排列在所有由小到大全排列中的顺序,因此是可逆的。
康拓展开:
给定一个全排列序列,求该序列是所有全排列序列中字典序第几的序列
公式如下:
其中, a[i] 为整数,并且 0<=a[i]<i,1<=i<=n。
- a[i]表示位于位置i后面的数小于a[i]值的个数。
- X为小于该排列的个数,所以该排列的次序应该是X+1。
康拓展开代码:
cin>>n; fac[0]=1; for(int i=1;i<=n;i++)//预处理阶乘 fac[i]=fac[i-1]*i; int ans=0; for(int i=1;i<=n;i++) cin>>a[i]; for(int i=1;i<=n;i++){ int k=0; for(int j=i+1;j<=n;j++) if(a[j]<a[i])k++; ///统计位于a[i]后且比a[i]小的数的个数 ans+=k*fac[n-i]; } cout<<ans+1<<endl; ///注意,记得+1
逆康拓展开:
给定全排列大小n,字典序k,求字典序为k的排列。
逆康拓展开代码:
vector<int>y; void ni_Cantor(int len,int num) { num=num-1; ///注意 vector<int>a; for(int i=1;i<=len;i++) a.push_back(i); for(int i=1;i<=len;i++){ int t=num/ans[len-i]; num=num%ans[len-i]; y.push_back(a[t]); ///剩余数里第t+1个数为当前位 a.erase(a.begin()+t); ///删除选做当前位的数 } }
应用:
- 康托展开是一个数组到一个数的映射,可以应用于hash中进行空间压缩。例如,在八数码问题中,我们可以把一种排列状态压缩成一个整数存放在数组中。(获取排列的id,构建hash表)
- 计算关于排列序列的问题
康拓展开及逆康拓展开:
#include<iostream> #define _ ios::sync_with_stdio(false); using namespace std; int ans[12]; ///存储阶乘 void factorial(int q) ///预处理出0!~q! { ans[0]=1; for(int i=1;i<=q;i++) ans[i]=ans[i-1]*i; } /*康拓展开*/ int Cantor(int n,int x[]) ///n表示n个数的排列,x[]为传递过来的排列数组 { int cnt=0,sum; for(int i=1;i<=n;i++){ sum=0; for(int j=i+1;j<=n;j++){ if(x[j]<x[i]) sum++; } cnt+=sum*ans[n-i]; } return cnt+1; } /*逆康拓展开*/ int* ni_Cantor(int len,int num,int y[]) ///len表示len个数的排列,num表示次序,y[]存储生成的排列数组 { bool book[len+2]={0}; int sum2,k=0,t; num=num-1; for(int i=1;i<=len;i++){ sum2=0; t=num/ans[len-i]; num=num%ans[len-i]; for(int j=1;j<=len;j++) ///对比上面的逆康拓展开做法,利用vector的特性,而不需要去for嵌套,降低了复杂度 if(!book[j]){ sum2++; if(sum2==t+1){ y[k++]=j; book[j]=1; break; } } } return y; } int main(){_ factorial(10); ///预处理出0!~10! int T,a; cin>>T; ///T个测试用例 while(T--) { int x[15]={},y[15],n,a,m; cin>>a; ///a为0时,输出该排列的次序编号; ///a为1时,输出n个正整数,表示这个次序对应的一个全排列(每个数字后面跟一个空格)。 if(a==0){ cin>>n; ///0<n<10 for(int i=1;i<=n;i++) cin>>x[i]; cout<<Cantor(n,x)<<endl; } else if(a==1){ cin>>n>>m; ///n表示n个数的全排列,m表示次序编号为m的全排列 ni_Cantor(n,m,y); for(int i=0;i<n;i++) cout<<y[i]<<' '; cout<<endl; } } return 0; }
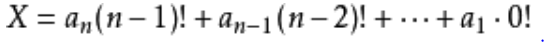



 浙公网安备 33010602011771号
浙公网安备 33010602011771号