常见曲线图

ROC（Receiver Operating Characteristics）

ROC曲线是一种用于评估分类模型性能的工具，特别是在不同的决策阈值下。ROC曲线显示了当阈值变化时，真正例率 (True Positive Rate, TPR) 和假正例率 (False Positive Rate, FPR) 之间的关系。在身份验证领域也可用来表示FAR（False acceptance rate）和FRR（False rejection rate）的关系。

在多数情况下，以FPR为横坐标，以TPR为纵坐标，在这样的设置下，曲线上的值越靠近左上角越好（表示被正确分类的值很高，被认为是正确但其实是错误的很少），同理，以FAR为横坐标，以FRR为纵坐标亦是可以的。

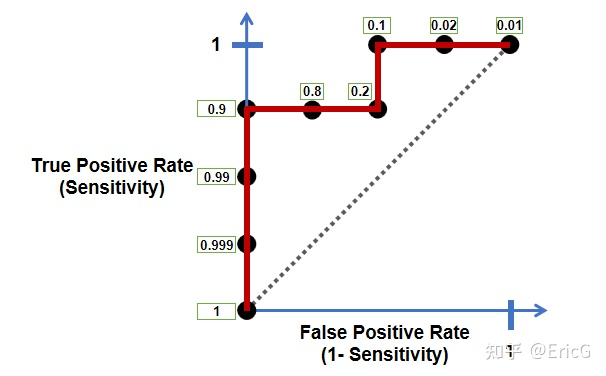
 （此时图上的任一值都表示某“模型”的一个阈值/配置）

AUC (Area Under the ROC Curve)

AUC是ROC曲线下的面积，它提供了一个单一的值来评估分类模型的性能。AUC的值介于0和1之间：

• AUC = 0.5：模型的预测能力等同于随机猜测。
• AUC = 1.0：模型在所有阈值下都有完美的预测性能

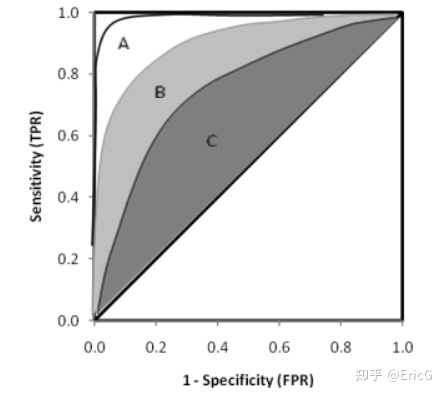
以该图为例，性能上或者说预测精度上：配置A>配置B>配置C

以上配置来说，是以FPR为x轴，TPR为y轴为设置的，若是以其他情况可能另有说法，比如在

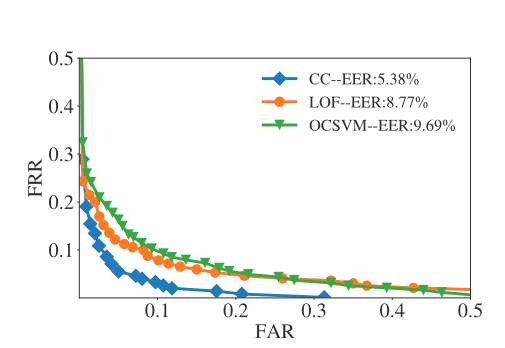
 很明显左下角方向更具有优势，在此时，AUC面积越小越好，即CC模型更有优势

 PDF(Probability Density Function)

概率密度函数，是一个描述连续随机变量在某一特定值的概率的函数。它用于连续概率分布。在机器学习和深度学习中，连续随机变量的概率密度函数可以用于似然估计、生成模型等。

假设是某一概率密度函数

• 始终非负
• 对整个定义域积分时，总和为1（积分面积为1）

常见的PDFs：正态分布、指数分布、Beta分布

 与之对应的是PMF (Probability Mass Function) 描述的是离散随机变量的概率分布，这里按下不表。

CDF (Cumulative Distribution Function)

累积分布函数，描述了一个随机变量小于或等于某一特定值的概率。它适用于离散和连续的随机变量。在机器学习和模拟中: CDF常用于生成服从特定分布的随机样本，或为某些算法（如决策树）确定数据分割点。

• 有界性：对于所有的x，CDF的值始终在0和1之间。
• 单调性:CDF是非递减的，即如果 a≤b，那么 CDF(a)≤CDF(b)。
• 右连续性

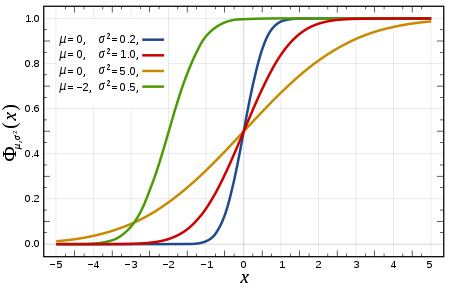
 文字描述略微歧义，其实是在定义域从左到右概率的累计和，队长上一项PDF观察图像理解更简单。

 

 

 

参考：https://zhuanlan.zhihu.com/p/573964757