KL散度
KL散度的用途
用来衡量真实分布和近似分布之间的差距（两个数据分布之间的距离）
KL散度的定义
连续变量：
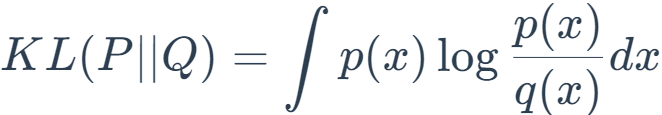
离散变量：
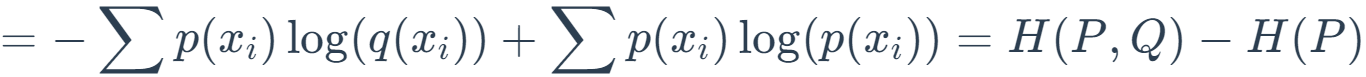
其中 q(x) 是近似分布，p(x) 是真实分布。直观地说，这衡量的是给定任意分布偏离真实分布的程度。如果两个分布完全匹配，DKL=0，否则它的取值应该是在 0 到无穷大（inf）之间。KL 散度越小，真实分布与近似分布之间的匹配就越好。
公式解释
* 公式中H(P,Q)项称作P和Q的交叉熵（cross entropy），而H(P)就是熵。在信息论中，熵代表着信息量，H(P)代表着基于P分布自身的编码长度，也就是最优的编码长度（最小字节数）。而H(P,Q)则代表着用Q的分布去近似P分布的信息。两个分布差异越大，则需要的编码长度也就越长。所以两个值的差就代表冗余的编码长度，也就是两个分布的差异程度。所以KL散度在信息论中还可以称为相对熵（relative entropy）。
* KL散度并不是直接的距离度量，因为即P对于Q的KL散度不等于Q对于P的KL散度，亦可说KL散度不是对称的
* 关于KL散度的非负性证明
关于凸函数
关于JENSON不等式：Jensen不等式是关于凸函数和期望值的一个基本不等式。如果你有一个凸函数f（或凹函数），Jensen不等式提供了一个方法来界定函数的期望值与函数的值的期望之间的关系。
证明过程：
参考：https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247505205&idx=7&sn=5993af5de9fd2e7294ca9a27da26f31f&chksm=ebb7ede1dcc064f76e1fecd3e617f1fffc2bc4590bf9e07276cfebf2c6264a28185b458d66f4&scene=27
参考：https://aistudio.baidu.com/projectdetail/5225071
参考：https://www.bilibili.com/read/cv21701321/
