什么是范数：L0、L1、L2、....、Lp
在机器学习和数据科学中，范数常常被用来作为正则化项，防止模型过拟合，或者用来衡量模型复杂度。
具体来说，范数（Norm）是一种测量向量“长度”或“大小”的函数。范数需要满足一些性质，包括：
- 非负性：对任意向量v，范数都是非负的，即||v|| >= 0，且当且仅当v=0时，||v|| = 0
- 一致性：对任意标量a和任意向量v，有||av|| = |a|*||v||
- 三角不等式：对任意向量u和v，有||u + v|| <= ||u|| + ||v||
L0范数
L0范数定义为向量中非零元素的个数。
例如，向量[0, 1, 2, 0, 3]的L0范数就是3，因为它有3个非零元素。
L0范数常常用来表示模型的复杂性或者模型的稀疏性。例如，如果你想要构建一个稀疏的模型（即模型中的大部分参数都是0），你可能会试图最小化模型参数的L0范数。然而，L0范数的问题在于它是非凸的，这使得相关的优化问题变得非常困难。因此，在实际应用中，人们常常使用L1范数来代替L0范数，因为L1范数在保持稀疏性的同时，其优化问题是凸的，更容易求解。
L1范数
L1范数，也被称为曼哈顿距离或者绝对值和，是向量中所有元素的绝对值之和。
对于一个n维向量x = [x1, x2, ..., xn]，其L1范数可以表示为： ||x||1 = |x1| + |x2| + ... + |xn| 例如，向量[1, -2, 3, -4]的L1范数就是1+2+3+4=10
L1范数在机器学习和数据科学中有很多应用。例如，在线性回归模型中，L1范数可以用来进行特征选择和生成稀疏模型。当我们将L1范数作为正则化项加入到模型的损失函数中，这种方法被称为Lasso回归。L1范数因为其产生稀疏解的特性，是一种常用的特征选择方法，可以用来剔除不重要的特征。
L2范数
L2范数是一种衡量向量大小的方法，也被称为欧几里得范数或者欧几里得长度。L2范数就是向量元素平方和的平方根。
对于一个n维向量x = [x1, x2, ..., xn]，其L2范数可以表示为： ||x||2 = sqrt(x1² + x2² + ... + xn²) 向量[1, 2, 3]的L2范数就是sqrt(1² + 2² + 3²) = sqrt(14)。
在线性回归模型中，L2范数可以用来进行正则化，防止模型过拟合。当我们将L2范数作为正则化项加入到模型的损失函数中，这种方法被称为岭回归或者L2正则化。L2正则化的效果是使得模型的权重向量尽可能小，从而限制了模型复杂度，提高了模型的泛化能力。
L1和L2的区别
稀疏性：
- L1范数正则化能够产生稀疏的权重矩阵，即其解的许多元素为0。这一特性使得L1范数正则化成为一种有效的特征选择方法。
- L2范数正则化则不具备这种性质，它会尽可能地缩小所有权重的大小，但不会将它们压缩到零。
解的稳定性：
- L1范数正则化可能产生不稳定的解，即微小的数据变动可能导致解的大幅度变化。
- 相比之下，L2范数正则化会产生更稳定的解，对数据的微小变动更加鲁棒。
解的唯一性：
- L1范数正则化可能存在多个解，因为L1范数的等高线在高维空间中形状为菱形，这可能会与损失函数的等高线在某些顶点相交，形成多个最优解。
- 相比之下，L2范数正则化总是有唯一解，因为L2范数的等高线在高维空间中形状为球形，与损失函数的等高线只有一点交点。
Lp范数
Lp范数是L1范数和L2范数的一种泛化，它定义为向量中所有元素的p次方之和的1/p次方。
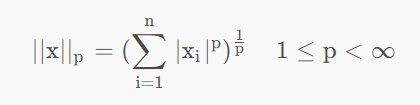
p可以是小数，但是不能是无穷，对于无穷范数有额外的定义
结合范数图像了解参数优化
对于一个二维的范数图像来看，p越大，范数图像越呈现正方形，L1范数是菱形，L2范数是圆形
在深度学习/机器学习中，Lp范数往往是作为一个正则化项加在损失函数的后面用以优化参数，L1（黑色菱形）与参数权重（彩色等高线）相交之处多是在坐标轴上，所以多产生稀疏矩阵；L2范数（黑色圆形）与参数矩阵多相交在较低值参数区域，所以能防止一些较大参数的产生，平滑的优化参数。
然后举一个数学原理上的例子
假设我们有一个线性回归模型，其损失函数为平方误差损失，形式如下：
其中，N是样本数量，y_i是第i个样本的真实值，\hat{y}_i是模型对第i个样本的预测值。
如果我们向这个损失函数添加L2正则化项，损失函数将变为：
其中，p是模型的参数数量，w_j是第j个参数的值，λ是正则化参数，它控制正则化项的强度。注意，这里的正则化项是所有参数值的平方和，这是L2正则化的特点。
在没有正则化的情况下，SGD的更新规则如下：
其中，α是学习率，也就是参数每次更新的步长；∂L/∂w_j 是损失函数L关于参数w_j的偏导数，它表示损失函数在当前参数值下的梯度。
如果我们向损失函数添加L2正则化项，那么SGD的更新规则将变为：
可以看到，现在的更新规则多了一个αλw_j的项，这个项就是L2正则化的影响。这个额外的项会减小参数的值，从而鼓励模型选择较小的参数。这就是L2正则化在参数更新时的作用。
在直观上理解，这个额外的更新项相当于每次在更新参数后，都将参数向零收缩一定的比例。这个比例由正则化参数λ和学习率α决定。这种向零收缩的效果就是L2正则化防止过拟合的主要机制
