相似性-距离方法一览
相似性计算指的是度量两个对象之间相似程度的过程，而距离计算则是度量两个对象之间距离的过程。在某些情况下，它们是等价的，例如当距离越小表示两个对象越相似时，这时候可以将距离计算视为相似性计算的一种形式。
然而，在一些情况下，相似性计算和距离计算是不同的。例如，当度量两个对象之间的相似程度时，可以使用余弦相似度等指标。在这种情况下，计算的不是距离，而是两个对象之间的夹角余弦值。
总的来说，相似性计算和距离计算之间的关系取决于具体的应用场景和使用的度量指标。在许多情况下，它们是等价的，但在其他情况下，它们可能是不同的。
相似性计算方法
余弦相似性（Cosine Similarity）
余弦相似性是指两个向量在空间中的夹角余弦值，夹角越小表示两个向量越相似，夹角越大表示两个向量越不相似。
如果两个向量夹角为90度，那么它们之间的余弦相似度为0，表示它们没有任何相似性。
如果两个向量夹角为0度，那么它们之间的余弦相似度为1，表示它们非常相似。
如果两个向量夹角为180度，那么它们之间的余弦相似度为-1，表示它们非常不相似。
举一个最简单的例子：
有两个特征向量：A' = [1, 2, 3, 4, 5, 6, 7, 8]， B' = [2, 2, 2, 2, 1, 1, 1, 1]（这两个向量都是高维向量展成的一维，维度相同）
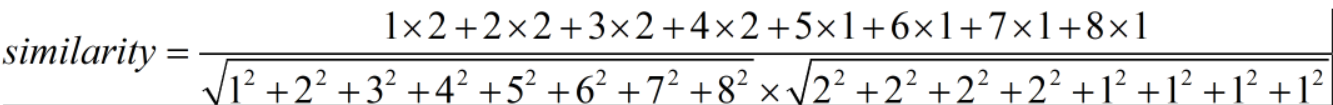
调整余弦相似度（Adjusted Cosine Similarity）
对于某些情况下（比如一个人对两个电影的评分，A（1，2），B（8，9），这说明A和B是十分不相似的），需要先对两个张量对象的数值进行一些调整。
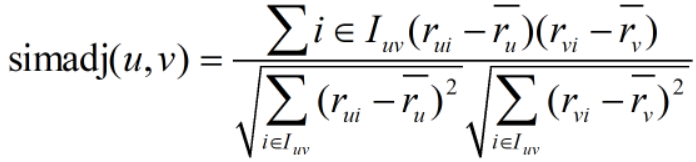
\bar ru和\bar rv和是其对应维度的平均值，其实就是将其中心化。
欧几里得距离
皮尔逊相关系数
