多种归一化和标准化方法区别
归一化和标准化有什么区别？
归一化(N o r m a l i z a t i o n NormalizationNormalization)：将一列数据变化到某个固定区间(范围)中，通常，这个区间是[0, 1]，广义的讲，可以是各种区间，比如映射到[0，1]一样可以继续映射到其他范围，图像中可能会映射到[0,255]，其他情况可能映射到[-1,1]；
标准化(S t a n d a r d i z a t i o n StandardizationStandardization)：将数据变换为均值为0，标准差为1的分布切记，并非一定是正态的；需要强调的是：标准化虽然有强调均值和标准差的变化，但是其分布种类并没有变化，若原来数据是卡方分布，则标准化之后仍是卡方分布。
（待完善：分布的概念和种类，以及后面强调的例子）
中心化：另外，还有一种处理叫做中心化，也叫零均值处理，就是将每个原始数据减去这些数据的均值。
归一化
Batch Normalization
简单的说，BN可以在不影响精度的情况下加速神经网络的训练收敛，具体的实现也比较简单，但是就可解释性来说依旧众说纷纭，有一个说法是加入了一定的噪音，因为对于不同的Batch来讲，它的分布有可能机器不同，在归一化之后又限定了数据的范围，当然这是其中一种说法，像原论文提出是为了减少内部协变量转移，后来有人指出其实并没有做到这件事（炼丹嘛~），无论怎么样，BN这个技术目前使用的比较多，而且效果比较好，暂且为功能性使用来讲不去深究内部原因。
简单来说，BN是把一个批次的数据，在特征维度间进行归一化。举个例子来说，假设一个集体中的个人有身高体重发量三个维度，那么BN会分别在不同样本间的身高、体重、发量三个方面进行归一化。分为以下两步：
第一步：主要是计算输入批次的均值和方差，然后把数据归一化到均值为0，方差为1的数据分布。
第二步（可选）：第二步会有一个反归一化，因为不一定均值为0，方差为1的分布就是好的，γ和β是两个可学习参数，用于控制方差和均值的转移。（这一步在设置BN代码中可选是否有可训练的参数）
使用
- 全连接层和卷积层输出上，激活函数前
- 全连接层输入上，作用在特征维度
- 卷积层输入上，作用在通道维
验证
这里简单使用torch中自带的来验证
import torch import torch.nn as nn #随机生成数据张量 feature = torch.randn(3,5) #batch_num, dim_num #设置BN函数 bn = nn.BatchNorm1d(5, affine=False) #打印原来的张量的平均值 sum_tensor = feature.mean(dim=0) print(feature) print(f'归一化之前的均值{sum_tensor}，方差：{feature.var(dim=0)}') #打印归一化后的平均值和方差 out = bn(feature) sum_out = out.mean(dim=0) print(out) print(f'归一化之后的均值{sum_out}，方差：{out.var(dim=0)}')
这里可以看到均值均近似为0，不过不知道为什么方差为都近似等于1.5；nn.BatchNorm1d有很多变种和参数可选。
Layer Normalization
当输入样本间长度不一时，需要对样本进行padding，而padding的值在BN归一化时会引入很大的偏差。所以这时候应该使用LN效果会好一点，在以后轨迹数据方面可能要多使用的时LN。
需要注意的是，BN中训练时需要累计moving_mean和moving_var两个变量，所以BN中有4个参数。而LN只要累计两个参数即可。
在公式方面，LN和BN并无太多差别。
验证
import torch import torch.nn as nn feature = torch.randn(5,3) print(feature) print(f'层归一化之前的均值{feature.sum(dim=1)}，方差：{feature.var(dim=1)}') ln = nn.LayerNorm(normalized_shape=[3], elementwise_affine=False) out = ln(feature) print(out) print(f'层归一化之后的均值{out.sum(dim=1)}，方差：{out.var(dim=1)}')
这里值得注意的是normalized_shape的设置，要从最后一个维度往前进行设置，且不是设置序号而是维度的大小，并且仅设置最后一个维度比较符合对一个单独的样本之间不同的维度进行归一化。
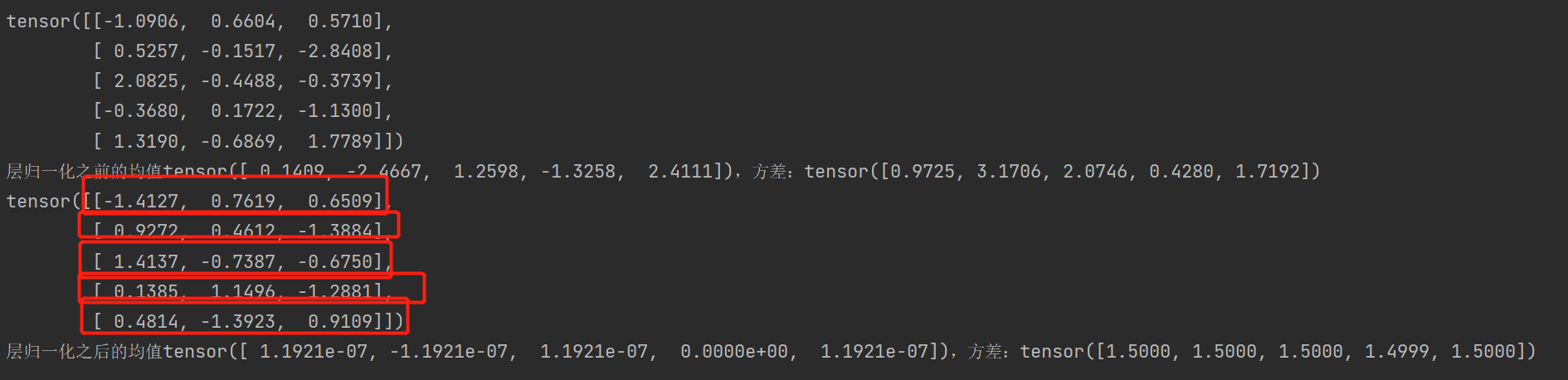
可以看到，每一个样本不同维度见进行了归一化，目前来讲，可以大概把shape当作一个两维的，即一个batch_size,dim_size,这样只对最后一维归一即可。
Instance Normalization
IN常使用的场景是图像的风格化生成和迁移任务，目的是关注一张图片中每个像素的平均。在这里我将图像和轨迹做一个类比：
轨迹 VS 图像
N：一个批次内是多个轨迹/多张图像
HxW：一个样本由多个轨迹点组成/多个像素点组成
C：一个轨迹点/像素点有多个特征（经纬度、时间/颜色通道）
所以在关注单个样本之间的差距时，也许使用IN有一些在考虑的情况
标准化
数据标准化处理主要包括指标一致化处理和无量纲化处理两种类型。这里关注无量纲化处理方法
数据无量纲化处理，主要解决数据之间可比性的问题，这也是我们对数据进行标准化处理的最主要的一个目的。
在实际的应用中，由于不同变量自身的量纲不同，数量级存在较大差异，在进行综合评价时，不同变量所占的作用比重也会有所不同。例如，某个变量的数值在1-10之间，而另一个变量的数值范围在100-1000之间，此时若进行综合评价，从数值的角度，很有可能数值变化范围大的变量，它的绝对作用就会较大，所占的比重较大。
因此，为了消除量纲、变量自身变异和数值大小的影响，比较不同变量之间的相对作用，就需要对数据进行无量纲化处理，将其转化为无量纲的纯数值来进行评价和比较。
Z-score标准化法
当我们遇到某个指标的最大值和最小值未知的情况时，或者有超出取值范围的离群数值的时候，就不再适宜计算极差了，此时我们可以采用另一种数据标准化最常用的方法，即Z-score标准化，也叫标准差标准化法。
具体的步骤为：
( x为原数据，μ为均值，σ为标准差，z为标准化后的数据)
经过Z-score标准化后，数据将符合标准正态分布，即将有约一半观察值的数值小于0，另一半观察值的数值大于0，变量的均值为0，标准差为1，变化范围为-1≤z≤1。
Min-Max 标准化
Min-Max 标准化将原始数据线性地转化到一个预定的最小值和最大值之间，通常是 0 到 1。
- d'pi：代表经过 Min-Max 标准化后的值
- di：代表原始数据值
- dmin：代表原始数据的最小值
- dmax：代表原始数据的最大值
将特征值缩放到 0 到 1 的范围，使得各特征具有统一的比例尺度，有助于防止某些特征在计算中过于主导,不改变原始数据的分布, 当新的数据点超出原始数据的最小值或最大值时，需要重新进行标准化，或者数据将被压缩在原定的范围之外。
受异常值的影响大，极端值或者离群值会对最小值和最大值产生影响，从而影响标准化的结果。不能保证标准化后的数据均值为0，标准差为1，所以如果需要的是标准正态分布的数据，这种方法就不适用。
参考：https://cdn.modb.pro/db/488021
