树网的核
[NOIP2007 提高组] 树网的核
题目描述
设 \(T=(V,E,W)\) 是一个无圈且连通的无向图(也称为无根树),每条边都有正整数的权,我们称 \(T\) 为树网(treenetwork),其中 \(V\),\(E\) 分别表示结点与边的集合,\(W\) 表示各边长度的集合,并设 \(T\) 有 \(n\) 个结点。
路径:树网中任何两结点 \(a\),\(b\) 都存在唯一的一条简单路径,用 \(d(a, b)\) 表示以 \(a, b\) 为端点的路径的长度,它是该路径上各边长度之和。我们称
\(d(a, b)\) 为 \(a, b\) 两结点间的距离。
\(D(v, P)=\min\{d(v, u)\}\), \(u\) 为路径 \(P\) 上的结点。
树网的直径:树网中最长的路径成为树网的直径。对于给定的树网 \(T\),直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距 \(\mathrm{ECC}(F)\):树网 \(T\) 中距路径 \(F\) 最远的结点到路径 \(F\) 的距离,即
\(\mathrm{ECC}(F)=\max\{D(v, F),v \in V\}\)
任务:对于给定的树网 \(T=(V, E, W)\) 和非负整数 \(s\),求一个路径 \(F\),他是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过 \(s\)(可以等于 \(s\)),使偏心距 \(\mathrm{ECC}(F)\) 最小。我们称这个路径为树网 \(T=(V, E, W)\) 的核(Core)。必要时,\(F\) 可以退化为某个结点。一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
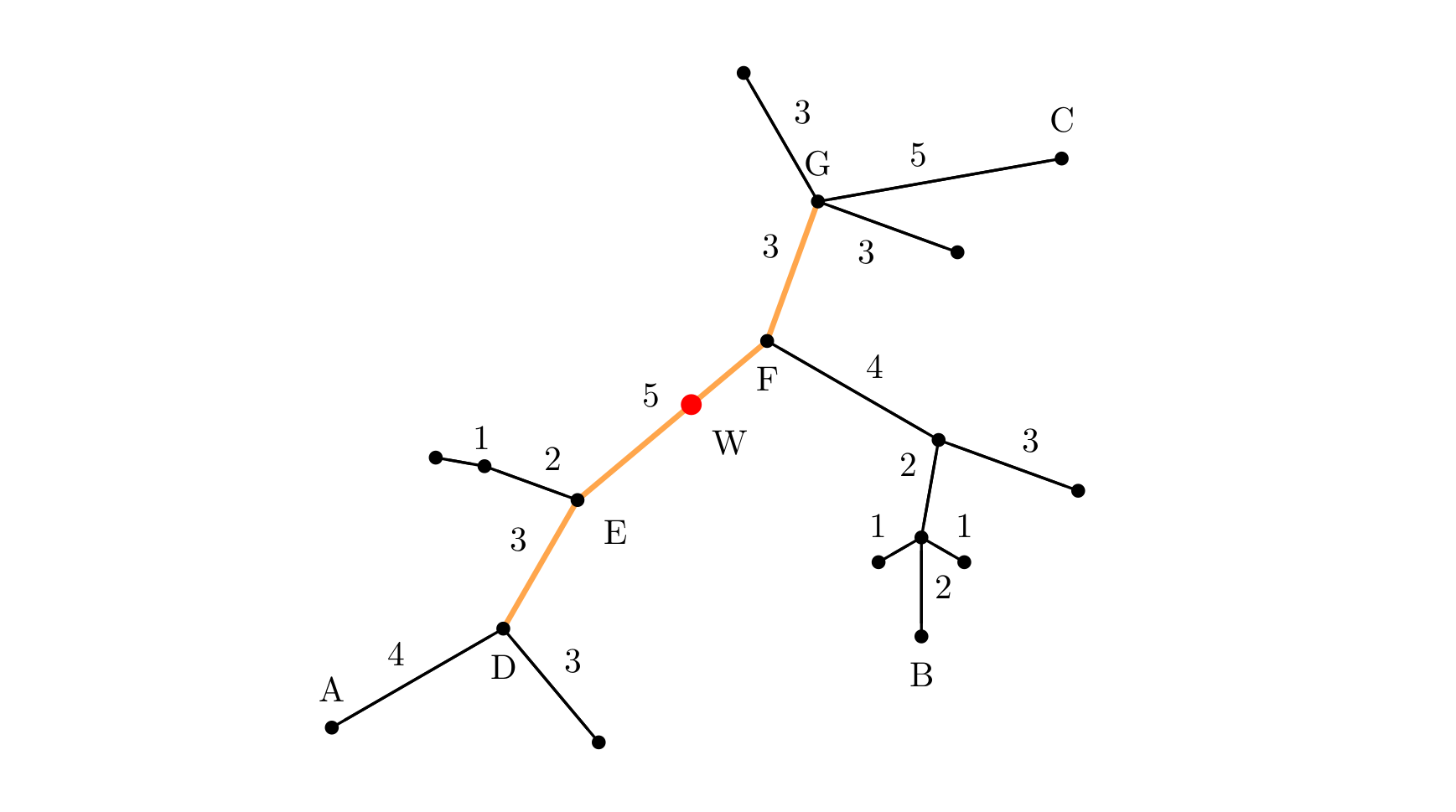
下面的图给出了树网的一个实例。图中,\(A-B\) 与 \(A-C\) 是两条直径,长度均为 \(20\)。点 \(W\) 是树网的中心,\(EF\) 边的长度为 \(5\)。如果指定 \(s=11\),则树网的核为路径DEFG(也可以取为路径DEF),偏心距为 \(8\)。如果指定 \(s=0\)(或 \(s=1\)、\(s=2\)),则树网的核为结点 \(F\),偏心距为 \(12\)。
输入格式
共 \(n\) 行。
第 \(1\) 行,两个正整数 \(n\) 和 \(s\),中间用一个空格隔开。其中 \(n\) 为树网结点的个数,\(s\) 为树网的核的长度的上界。设结点编号以此为 \(1,2\dots,n\)。
从第 \(2\) 行到第 \(n\) 行,每行给出 \(3\) 个用空格隔开的正整数 \(u, v, w\),依次表示每一条边的两个端点编号和长度。例如,2 4 7 表示连接结点 \(2\) 与 \(4\) 的边的长度为 \(7\)。
输出格式
一个非负整数,为指定意义下的最小偏心距。
样例 #1
样例输入 #1
5 2
1 2 5
2 3 2
2 4 4
2 5 3
样例输出 #1
5
样例 #2
样例输入 #2
8 6
1 3 2
2 3 2
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3
样例输出 #2
5
提示
- 对于 \(40\%\) 的数据,保证 \(n \le 15\)。
- 对于 \(70\%\) 的数据,保证 \(n \le 80\)。
- 对于 \(100\%\) 的数据,保证 \(2\le n \le 300\),\(0\le s\le10^3\),\(1 \leq u, v \leq n\),\(0 \leq w \leq 10^3\)。
NOIP2007 提高组第四题
题目好长。。
其实很简单,很明显就是直径。
假如从直径上的一个点出发,能够找到一个比这个点到直径的两头的点更远的点,那这个就和直径的定义是矛盾的。
所以其实我们要做的就是从直径的头走到尾,找出里面比s小的所有段,然后每一段的离心距其实就是这段开头和结尾的分别到对应的直径的端点的距离和这段直径上每个点不经过直径上其他的点能够达到的距离的max
\(O(n)\)可以解决。
写法可以很简单,这篇总结主要就是写法。
原本我是写了两个bfs+一个dfs,前两个是统计距离某个点距离最大的点在哪里,来求直径,后面的是求从某个点出发不经过直径上的点,能够达到的距离它最远的点的距离是多少。
然后就巨长,写了150行。。
难绷。
这下是真oi新手了
其实完全没有必要,上面三个函数的功能一个函数可以实现,只需要写一个能够统计每个点到它的子树里面的距离的最大值的函数就好了,统计距离最远的点的功能完全是可以附带的。然后加一个vis数组,在计算的时候顺带记录一下父亲节点,这样就能够把直径全部标记了,并且形成一个类似链表的东西。
然后是对于统计截取的树核上的非树核端点的点的偏心距,这个。。其实可以发现,最大值如果出现在这个部分,那我们其实只需要分别对每个点统计就好了,没必要用单调队列在中途动态统计最大值,如果不产生在这个部分,那就是树核端点到离他最近的直径端点的距离作为答案,那更是没有必要了。
所以其实这个单调队列只是比较符合思维的逻辑,分析过后可以发现是完全没有必要的东西。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
char c=getchar();int a=0,b=1;
for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;return a*b;
}
int head[601],tot,Max,Maxid,dist[301],vis[301];
struct edge
{
int next,to,v;
}e[601];
int n,s;
inline void add(int i,int j,int v)
{
e[++tot].next=head[i];
e[tot].to=j;
e[tot].v=v;
head[i]=tot;
}
int d[301],f[301],top;
void dfs(int x,int fa)
{
f[x]=fa;
if(dist[x]>dist[Maxid])Maxid=x;
for(int i=head[x];i!=0;i=e[i].next)
{
int u=e[i].to;
if(vis[u]==1||u==fa)continue;
dist[u]=dist[x]+e[i].v;
dfs(u,x);
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n=read(),s=read();
for(int i=1;i<n;i++)
{
int x=read(),y=read(),z=read();
add(x,y,z);add(y,x,z);
}
dist[1]=0;dfs(1,0);
dist[Maxid]=0;dfs(Maxid,0);
top=Maxid;
int x=0,ans=0x3f3f3f3f;
for(int i=top,j=top,l=1,r=0;i;i=f[i])
{
while(dist[j]-dist[i]>s)j=f[j];
x=max(dist[top]-dist[j],dist[i]);
ans=min(ans,x);
}
// cout<<ans<<endl;
memset(vis,0,sizeof(vis));
for(int i=top;i!=0;i=f[i])vis[i]=1;
for(int i=top;i!=0;i=f[i])
{
Maxid=i;
dist[i]=0;
dfs(i,f[i]);
}
for(int i=1;i<=n;i++)
{
ans=max(ans,dist[i]);
}
cout<<ans<<endl;
return 0;
}
这个思路是真的真的很好,我很多时候的代码就是因为实现的思路不够简洁导致代码需要调很久,一个简洁的思路是真的非常非常大的一个优势。
我觉得这个其实是一个习惯和经验,就是要靠养成和积累的。所以这篇总结就是在积累这个经验。
这份代码的实现思路来自洛谷题解。真的很值得学习。

