斜率优化入门任务分配

终于开始斜率优化了。。
洛谷P2365 任务安排

题目描述

从零时刻开始，这些任务被分批加工，第

每个任务的费用是它的完成时刻乘以一个费用系数

输入格式

第一行一个正整数

下面

输出格式

一个数，最小的总费用。

输入输出样例

输入 #1

输出 #1

说明/提示

【数据范围】
对于

【样例解释】
如果分组方案是

朴素方程很简单，f[i][j]表示把前i个任务分为j组的时候的最小代价
转移显然
这题要求O(n^2),这种转移是O(n^3),不能通过
这边还是把方程写出来了

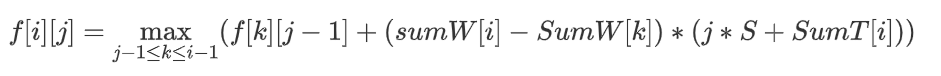
额，j只和j-1有关，可以优化一维的空间
但是这边没什么必要
考虑优化
有j*SumW[i]这一项，无法单调队列优化
考虑我们要j这一维度的作用，是为了统计S来消除分组带来的后效性
但是仔细考虑，发现这个后效性是可统计的，也就是可以消除
我们每一次分组，增加了S的时间，只需要加上这个S导致的增加的代价即可
所以j这一维可以优化

状态设计变为:
f[i]表示把前i个任务分为了若干组时，算上罚时导致后面的分组代价增加后最小的代价为多少

转移方程变为

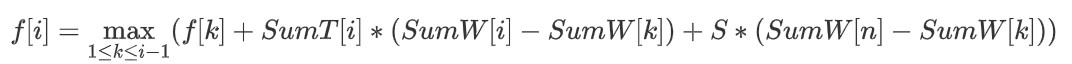
时间复杂度变为了O(n^2)

这是一个很重要的方法，通过提前统计所有可统计的后效性来优化dp
使用条件还是挺苛刻的，要求一个维度所代表的后效性可统计
多注意一下就好了，算是提供了一种新的优化思路

但是这题时一道斜率优化例题。。
O(n^2)并不是极限
额，方程变个形

假设k是我们的最优决策点，所以不用管ma
（可以去luogu看这题的题解，讲的很好
我们只需要维护一个决策点的下凸壳，这样里面放的决策点就都是最优决策的候选项
注意开longlong
斜率优化尽量写成相乘的模式，相除容易导致精度的损失而决策错误
因为相乘的原因，所以容易需要开longlong，要注意
正常的情况下，这个队列里面的决策是都需要保留的，但是这题的斜率比较特殊，是SumT[i]+S，显然，随着i的增加，它是单调递增的，所以前面的决策可以直接出队排除
如果不是单调递增的，那么就需要用二分查找来在这个队列里面logn找到需要的决策
还是非常快的

斜率优化。。几乎已经是线性dp的极限了吧？
在求最优解的dp中，结合上线性规划和单调队列的斜率优化，真的是。。
很难理解，也很神奇
使用条件和单调队列有些相似，决策区间单调移动，但是转移方程的形式更加的没有限制，单调队列优化更像是斜率优化的特殊情况

既然i和j的乘积现在也能够考虑了，那，如果是i*i*j或者类似的形式？
i的次方在斜率的部分，这个倒是直接计算就ok，如果是j的次方好像也没什么问题啊
主要是f[j]不太能有次方？假如两边开根号，仿射变换后的坐标系直线会变成斜线，斜率优化就不可能可以用了。。因为线性规划在这样的坐标系里面废掉了
那如果我不开次方，留着呢?
好像可以啊
f[i]在截距里面其实没什么变化，一样转移啊
可以的

这题的代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
    char c=getchar();int a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;return a*b;
}
ll n,S,SumT[5001],SumW[5001],f[5001],q[5001];
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read();S=read();
    for(int i=1;i<=n;i++)
    {
        SumT[i]=SumT[i-1]+read();
        SumW[i]=SumW[i-1]+read();
    }
    memset(f,0x3f,sizeof(f));
    f[0]=0;
    int l=1,r=1;
    for(int i=1;i<=n;i++)
    {
        while(l<r&&(f[q[l+1]]-f[q[l]])<=(S+SumT[i])*(SumW[q[l+1]]-SumW[q[l]]))l++;
        f[i]=f[q[l]]+SumT[i]*(SumW[i]-SumW[q[l]])+S*(SumW[n]-SumW[q[l]]);
        while(l<r&& (f[i]-f[q[r]])*(SumW[q[r]]-SumW[q[r-1]]) <= (f[q[r]]-f[q[r-1]])*(SumW[i]-SumW[q[r]]) )r--;
        q[++r]=i;
    }
    cout<<f[n]<<endl;
    return 0;
}

但是还没有结束
这题是斜率优化的例题，但是其实题目条件非常的仁慈
首先，看看方程

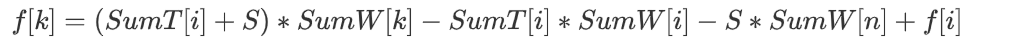
如果T[i]可以小于0怎么办？
T[i]小于0意味着SumT[i]并不一定是单调递增的，所以我们的决策点也不一定是在队伍里面单调移动
也就是队头的决策不一定是我们需要的（如果能用的话肯定是最优秀的，但是可能不能用）
我们需要用二分查找在队列里面找到一个位置，这个决策点和前面的点的斜率小于(SumT[i]+S)，而和后面的点的斜率则大于这个
然后用后面这个大于的点进行转移，这才是能用的转移

那如果T[i]保证大于0，w[i]可以小于0咋办？
W[i]小于0意味着我们计算出的f[i]在作为决策点的时候，并不一定是插入在队尾的
而是可以出现任意的两个点之间
所以我们可以用一个平衡树来维护这个队列，每一次计算完f[i]执行决策点的插入的时候，就直接查询就好了
总体复杂度多了一个logn,可以接受
这种情况下，平衡树自然也是支持二分查找的（怎么可能不支持）
所以其实T[i]也可以小于0
但是我们保证了T[i]大于0 ，这点是可以利用起来的
我们可以改写方程，让SumT[j]作为横坐标，这样的话每一次插入就一定是在队尾了
但是我想了想，发现我不会。。但是蓝书上是这么说的，到底怎么改写啊啊啊

总之，这些变形都可以满足，这说明了斜率优化的使用条件不是像这题的条件一样苛刻的，而是非常广的

posted @ 2023-11-26 15:19 HL_ZZP 阅读(8) 评论(0) 编辑收藏举报

刷新页面返回顶部

斜率优化入门 任务分配