单调队列优化多重背包
多重背包题目已经很熟了
我们要把它优化到O(nm)
也就是对于每一个物品,我们只能够对dp数组进行一次遍历,并且不能枚举取几个物品
或者说是,要在每一个状态下O(1)的找到取不同数量物品的最优解,并转移
我们可以发现,其实转移的区间是非常有规律的,f[j]只能够从f[j-v[i]],f[j-2*v[i]]....f[j-c[i]*v[i]]这几个状态转移
也就是一个有间隔的区间的最大值,如果区间范围是固定的,很明显是O(m)可以解决的
但是区间的范围是在单调的向左移动的,那就是对于每一个情况开一个单调队列就好
主要是观察转移的规律,抽象这个过程,发现特点,然后优化掉不必要的计算
比如这里就是优化掉了对每一个j的向前遍历寻找最优转移的操作,而是考虑直接动态维护这个决策区间的最大值
也就是所谓的O(1)转移
这也算是单调队列优化dp转移的一个本质了
只是这个复杂一些,开的空间多一些而已
没区别
整个单调队列优化dp的模型就是
f[i]=min(f[j]+val(i,j))(L[i]<=j<=R[i]),然后L,R是单调的,所有的单调队列优化dp都是从这个式子来的,只是一些变形,或者是添加一些复杂的东西
(比如那个平衡树和多重背包的多个单调队列)
但是如果拆开,还是这个式子
单调队列优化里面的val(i,j)拆开后,每一项都只能和i和j中的一个有关,否则维护的东西就只能对现在的状态有用,对于后面的转移则是没有帮助,那也没有优化的必要的了
说这个,其实是因为,其实这种也能维护,但是使用的不再是单纯的单调队列了
————————————————————————————————————————————————————————————————
过了几天的我,想了想,觉得我这个都不写,这种态度怎么学好。。
(然后发现我单调队列真的是学出了大问题)
这边再补一下吧
其实单调队列优化多重背包已经算是比较难的题目了(如果这个东西没有被做成例题的话)
我个人感觉对一个没有学过这个例题的人,这个能够达到紫题偏难的难度
因为这个单调队列优化不是写出来方程就能够看得出来的,方程是要二次加工改写的
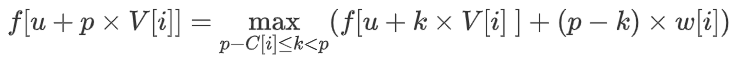
改写过是这个样子的,原本的我也写一下吧
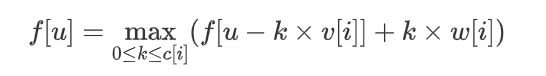
变化还是很大的,相当于是把转移的终点改写了,也只有这样才能单调队列优化
很明显,这不是普通的那么简单的单调队列优化,这个是要开c[i]个单调队列的
光这个变形就已经是挺难的了(套点东西还能更难)
但是唯一可以说的上巧妙的就是这个变形
只是这样的一点转移的规律,一些可能会重复进行的转移就能够用了
有了一些新的理解
单调队列几乎能优化掉所有的在边界变化单调移动的区间里面的最优值统计的转移,哪怕这个规律没有体现在所有的转移,而只是像这个题目里面的一样
对于几个部分是成立的
这很够了
难就难在,要注意到这个东西,就是在特殊的情况下也要注意到这个最值区间的重复
而这个东西,数据结构不好做,单调队列反而是得心应手
不知道除了这种多个单调队列的题目,有没有其他的,还挺期待的
代码
#include<bits/stdc++.h> #define ll long long using namespace std; inline int read() { char c=getchar();int a=0,b=1; for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1; for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;return a*b; } int n,m,f[1000001],v[10001],w[10001],c[10001],q[100001]; inline int calc(int i,int u,int k) { return f[u+k*v[i]]-k*w[i]; } int main() { // freopen(".in","r",stdin); // freopen(".out","w",stdout); n=read();m=read(); memset(f,0xcf,sizeof(f)); f[0]=0; for(int i=1;i<=n;i++) { v[i]=read(),w[i]=read(),c[i]=read(); for(int u=0;u<v[i];u++) { int l=1,r=0; int maxp=(m-u)/v[i]; for(int k=maxp-1;k>=max(maxp-c[i],0);k--) { while(l<=r&&calc(i,u,q[r])<=calc(i,u,k))r--; q[++r]=k; } for(int p=maxp;p>=0;p--) { while(l<=r&&q[l]>p-1)l++; if(l<=r)f[u+p*v[i]]=max(f[u+p*v[i]],calc(i,u,q[l])+p*w[i]); if(p-c[i]-1>=0) { while(l<=r&&calc(i,u,q[r])<=calc(i,u,p-c[i]-1))r--; q[++r]=p-c[i]-1; } } } } int ans=0; for(int i=1;i<=m;i++)ans=max(ans,f[i]); cout<<ans<<endl; return 0; }

