[NOIP2017 提高组] 宝藏

 

题目描述

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了 nn 个深埋在地下的宝藏屋， 也给出了这 nn 个宝藏屋之间可供开发的 mm 条道路和它们的长度。

小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远，也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏屋之间的道路无需再开发。

新开发一条道路的代价是 L×KL×K。其中 LL 代表这条道路的长度，KK 代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋） 。

请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代价最小，并输出这个最小值。

输入格式

第一行两个用空格分离的正整数 n,mn,m，代表宝藏屋的个数和道路数。

接下来 mm 行，每行三个用空格分离的正整数，分别是由一条道路连接的两个宝藏屋的编号（编号为 1−n1−n），和这条道路的长度 vv。

输出格式

一个正整数，表示最小的总代价。

输入输出样例

输入 #1

4 5 
1 2 1 
1 3 3 
1 4 1 
2 3 4 
3 4 1 
 

输出 #1

4

输入 #2

4 5 
1 2 1 
1 3 3 
1 4 1 
2 3 4 
3 4 2  

输出 #2

5

说明/提示

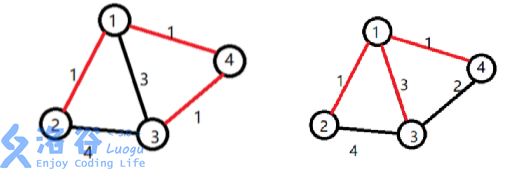
【样例解释 11】

小明选定让赞助商打通了 11 号宝藏屋。小明开发了道路 1→21→2，挖掘了 22 号宝藏。开发了道路 1→41→4，挖掘了 44 号宝藏。还开发了道路 4→34→3，挖掘了 33 号宝藏。

工程总代价为 1×1+1×1+1×2=41×1+1×1+1×2=4。

【样例解释 22】

小明选定让赞助商打通了 11 号宝藏屋。小明开发了道路 1→21→2，挖掘了 22 号宝藏。开发了道路 1→31→3，挖掘了 33 号宝藏。还开发了道路 1→41→4，挖掘了 44 号宝藏。

工程总代价为 1×1+3×1+1×1=51×1+3×1+1×1=5。

【数据规模与约定】

对于 20%20% 的数据： 保证输入是一棵树，1≤n≤81≤n≤8，v≤5×103v≤5×103 且所有的 vv 都相等。

对于 40%40% 的数据： 1≤n≤81≤n≤8，0≤m≤1030≤m≤103，v≤5×103v≤5×103 且所有的 vv 都相等。

对于 70%70% 的数据： 1≤n≤81≤n≤8，0≤m≤1030≤m≤103，v≤5×103v≤5×103。

对于 100%100% 的数据： 1≤n≤121≤n≤12，0≤m≤1030≤m≤103，v≤5×105v≤5×105。

---

upd 2022.7.27upd 2022.7.27：新增加 5050 组 Hack 数据。

我第一眼看到其实挺不会
但是n<=12太显然是状压了，很难有其他想法，那现在的问题就是怎么做？
首先作为一个dp，当然是要先找无后效性，并且能够保证在同一个状态下最佳balabala等的状态划分了
深度优先很明显是不现实的，不然就是一个暴力，复杂度我估算了是10的二十次方级别的
其实意思就是，这个dp必定有一个维度是当前子树的最大深度
还有一维自然是用二进制表示的当前状态了
然后仔细想想可以发现，转移的时候统计价值可能有点困难，因为我们状压dp转移的时候肯定是在枚举所有状态的，那我们怎么知道每一个新增加的节点的深度是多少？
（其实全部假设是最深的+1就好了
因为这样做肯定不会比原本更优秀，也就是不会影响到最优秀的答案，而如果不是连在最深的点上的话，那一定会有一个状态就对应了这种，然后这种转移到后面去的就一定会更优秀
可能有点抽象，但是仔细想想应该能明白，我们要做的就是保证最优解能够被转移到的同时不让假的最优解出现就好了，那我们就让这些假的最优解不优秀就好了
这真的是一个很方便很方便的思路，如果能学会的话，那之后很多时候写题目都会非常方便了。。
而且好调。。。（昨天写一个状压dp重构了3遍。。最后还是wa的，心态爆炸了）

状态和转移也还好，因为n真的很小很小，然后m很大，但是完全图也就那么点边，直接留下最小的，去个重，就是n方也是100而已，只要不是阶乘级别就能接受，真爽啊

写于一个半小时后——————————————————

然后！在我写完这篇博客，花半小时写了出来，花一个小时，把成个代码查了一整遍，发现我的位运算没加括号
啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
1个小时啊
寄
xdm位运算一定一定一定一定要加括号啊
然后在洛谷的hack数据1 0 下拿到了noip特有的95分ac
《孤岛忍宗堵门WA》
爱了

#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read() {
    char c=getchar();int a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;return a*b;
}
int n,m,len[13][13],tot;
struct edge
{
    int st,ed,v;
}e[1001],tur[1001];
bool mycmp(edge a,edge b)
{
    if(a.ed==b.ed&&a.st==b.st)return a.v<b.v;
    if(a.st==b.st)return a.ed<b.ed;
    return a.st<b.st;
}
int f[13][1<<12],Con[1<<12][1<<12];
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read();
    for(int i=1;i<=m;i++)
    {
        int a=read(),b=read(),c=read();
        if(a>b)swap(a,b);
        e[i].st=a;e[i].ed=b;e[i].v=c;
    }
    sort(e+1,e+1+m,mycmp);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            len[i][j]=-1;
        }
    }
    for(int i=1;i<=m;i++)
    {
        if(e[i].st!=e[i-1].st||e[i].ed!=e[i-1].ed)
        {
            tur[++tot].st=e[i].st;
            tur[tot].ed=e[i].ed;
            tur[tot].v=e[i].v;
            len[tur[tot].st][tur[tot].ed]=tur[tot].v;
            len[tur[tot].ed][tur[tot].st]=tur[tot].v;
        }
    }
//    {
//            int i=11,j=15;
//            int c1[13]={},c2[13]={},tot1=0,tot2=0;
//            for(int k=1;k<=n;k++)
//            {
//                if((i>>(n-k))&1)c1[++tot1]=k;
//                else
//                    if((j>>(n-k))&1)c2[++tot2]=k;
//            }
//            cout<<endl<<endl;
//            for(int k=1;k<=tot1;k++)cout<<c1[k]<<' ';
//            cout<<endl;
//            for(int k=1;k<=tot2;k++)cout<<c2[k]<<' ';
//            cout<<endl<<endl;
//    }
    for(int i=1;i<1<<n;i++)//³õʼ 
    {
        for(int j=1;j<1<<n;j++)//À©Õ¹ºó 
        {
            Con[i][j]=2147483647;
            if((i&j)!=i)continue;
            Con[i][j]=0;
            int c1[13]={},c2[13]={},tot1=0,tot2=0;
            for(int k=1;k<=n;k++)
            {
                if((i>>(n-k))&1)c1[++tot1]=k;
                else
                    if((j>>(n-k))&1)c2[++tot2]=k;
            }
            for(int k=1;k<=tot2;k++)
            {
                int minn=1000000;
                for(int h=1;h<=tot1;h++)
                {
                    if(len[c1[h]][c2[k]]!=-1)
                    minn=min(minn,len[c1[h]][c2[k]]);
                }
//                cout<<minn<<endl;
                if(minn!=1000000)
                Con[i][j]+=minn;
                else//˵Ã÷´ï²»µ½ 
                {
                    Con[i][j]=2147483647;
                    break;
                }
            }
        }
    }
    memset(f,0x3f,sizeof(f));
    for(int i=1;i<=n;i++)
    {
        f[1][1<<(i-1)]=0;
    }
    int ans=10000000;
    for(int i=2;i<=n;i++)
    {
        for(int j=0;j<(1<<n);j++)//ÉÏÒ»¸ö״̬ 
        {
            if(f[i-1][j]>100000000)continue;//¾ÍÊÇûÓÐÕâ¸ö״̬ 
            for(int k=0;k<(1<<n);k++)//ÏÂÒ»¸ö״̬ 
            {
                if((j&k)!=j)continue;
                if(Con[j][k]==2147483647)continue;
                f[i][k]=min(f[i][k],f[i-1][j]+(i-1)*Con[j][k]);
//                    cout<<f[i-1][j]<<' '<<(i-1)<<' '<<Con[j][k]<<' '<<f[i][k]<<endl;
                if(k==((1<<n)-1))
                {
                    ans=min(f[i][k],ans);
                }
            }
        }
    }
    if(m==0)ans=0;
    cout<<ans<<endl;
    return 0;
}