POJ 1390 Blocks

Blocks

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 7889		Accepted: 3210

Description

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:

Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.

Now let's look at the picture below:

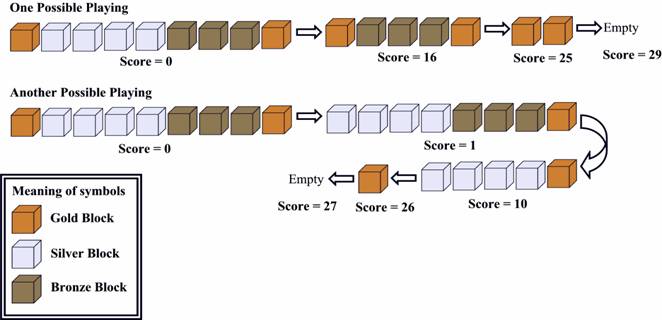
Figure 2

The first one is OPTIMAL.

Find the highest score you can get, given an initial state of this game.

Input

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.

Output

For each test case, print the case number and the highest possible score.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1

第一次看写了一个错的
因为没有考虑到如果有一个大块是由3个不同的小块合并得到的怎么办
代码长这样。。想是真的好像，写也是真的好写，wa on test2也是真的难绷

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cmath>
#include <math.h>
#include <string.h>
#define ll long long
using namespace std;
inline int read() {
    char c=getchar();int a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;return a*b;
}
int f[2001][2001],n,b[2001],a[2001],len[2001],tot;
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    int T=read();
    for(int cc=1;cc<=T;cc++)
    {
        n=read();
        tot=0;
        memset(f,0,sizeof(f));
        memset(len,0,sizeof(len));
        a[1]=b[1]=read();len[++tot]++;
        for(int i=2;i<=n;i++)
        {
            b[i]=read();
            if(b[i-1]==b[i])
            {
                len[tot]++;
            }
            else
            {
                a[++tot]=b[i];
                len[tot]++;
            }
        }
        for(int i=1;i<=tot;i++)f[i][i]=len[i]*len[i];
        for(int i=2;i<=tot;i++)//¼ä¸ô 
        {
            for(int l=1;l<=tot;l++)
            {
                int r=l+i-1;
                if(r>=tot)continue;
                if(a[l]==a[r])//Ò»ÖÖÇé¿ö 
                {
                    f[l][r]=max(f[l][r],f[l+1][r-1]+(len[r]+len[l])*(len[r]+len[l]));
                }
                for(int k=l;k<r;k++)//¼ä¶Ïµã 
                {
                    f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]);
                }
            }
        }
        cout<<"Case "<< cc <<": "<<f[1][tot]<<endl;
    }
    return 0;
}
/*
1
9
1 2 2 2 1 3 3 3 1


*/

 

hack数据就是在代码结尾的那个
在发现要考虑这种情况之后，我一脸懵逼。。（完全不应该）
其实不难，一步一步想就好了
我们要解决的其实就是多次合并的问题。。
很明显的解决办法就是增加状态。。
因为我们对f[i][r]的转移很明显已经没有办法了，新的转移只能通过新的状态了
而且需要使用dp是十分确定的，这题区间操作的后效性也直接决定了普通的线性dp无法解决，那既然它不是一道假题
那我们就通过状态来考虑怎么来计算这种情况
既然在完全计算完最优解之前，我们不确定它会不会在和其他的子串合并，那我们就记录一下可能会在被操作的地方的情况，方便后面的再次计算呗

设f[i][j][k]表示区间[i,j]在结尾有k个字符为a[j]的字符的时候的最优解

dp[i][p][k+len[j]]+dp[p+1][j][0]}

然后要用一个O（n）提前处理出来每一个点在它前面的和它颜色相同的点的位置
就能大约O（n^3）做了
（最近不知道为什么时间复杂度估计的是真的不准。。太奇怪了）
还学到了一种O（n）算每一个点在它前面的和它颜色相同的点的位置的方法。。
代码

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cmath>
#include <math.h>
#include <string.h>
#define ll long long
using namespace std;
inline int read() {
    char c=getchar();int a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;return a*b;
}
int f[201][201][201],n,b[501],a[501],len[501],pre[501],pos[501],tot;
int main()
{
//    freopen("1.in","r",stdin);
//    freopen("2.out","w",stdout);
    int T=read();
    for(int cc=1;cc<=T;cc++)
    {
        n=read();
        tot=0;
        memset(f,0,sizeof(f));
        memset(len,0,sizeof(len));
        memset(pre,0,sizeof(pre));
        memset(pos,0,sizeof(pos));
        a[1]=b[1]=read();len[++tot]++;
        for(int i=2;i<=n;i++)
        {
            b[i]=read();
            if(b[i-1]==b[i])
            {
                len[tot]++;
            }
            else
            {
                a[++tot]=b[i];
                len[tot]=1;
            }
        }
        for(int i=1;i<=tot;i++)
        {
            pre[i]=pos[a[i]];
            pos[a[i]]=i;
        }
        for(int len1=1;len1<=tot;len1++)
        {
            for(int l=1;l+len1-1<=tot;l++)
            {
                int r=l+len1-1;
                for(int k=0;k<=n;k++)
                {
                    f[l][r][k]=f[l][r-1][0]+(len[r]+k)*(len[r]+k);
//                    cout<<f[l][r][k]<<' ';
                    for(int i=pre[r];i>=l;i=pre[i])
                    {
                        f[l][r][k]=max(f[l][r][k],f[l][i][k+len[r]]+f[i+1][r-1][0]);
                    }
                }
//                cout<<endl;
            }
        }
        cout<<"Case "<< cc <<": "<<f[1][tot][0]<<endl;
    }
    return 0;
}
/*
1
8
3 3 3 2 3 3 3 3
*/

  这题。。
学会了和之前写过的区间dp都不一样的一种新形式
之前的两种一种是考虑区间的拆分点和合并
一种是考虑“最后一次操作”作为区间的拆分和合并点
这种。。
也不是不好拆分，主要特殊在它的决策需要考虑的范围
决策的类型很少，只有两种
想来想去，能总结的。。
于是不决，加状态！

怪哎
但是加个状态似乎是真的很好做。。。
也没有其他的办法了
然后就是这种在转移的时候在某些时候不考虑限制也是一个很好的思路
这是我之前没有遇到过的，积累积累