【高手训练】【RMQ】奶牛排队
第一题由于过水,就没写awa
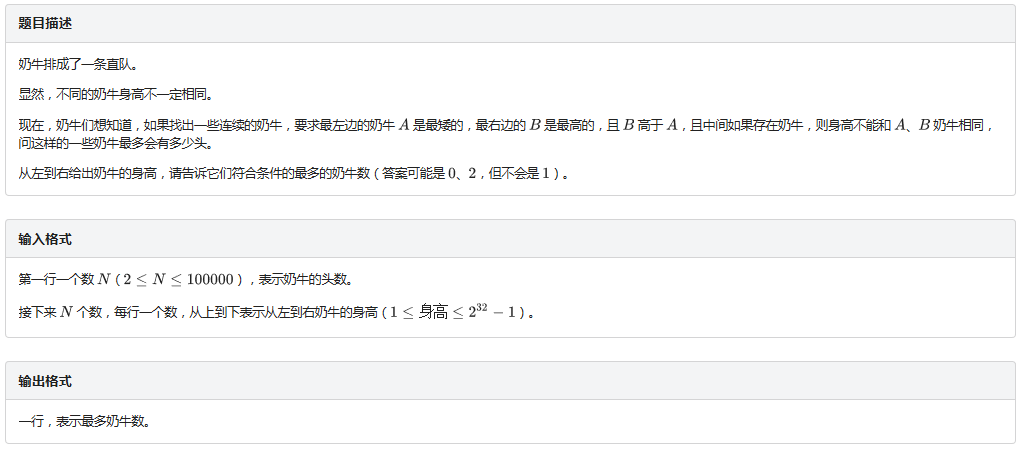

大概就是这样了。
题意就是求一个最长的区间使得区间的左边是它的最小值,区间右边是他的最大值
第一个想法肯定是暴力枚举啦awa
但是这个是O(n^3)的,绝对的不可过awa
思考性质awa
发现我们枚举每个区间的左右端点,其实有大量的不合法的计算的
也就是没有用的枚举。
考虑怎么避开不合法区间的枚举。
那么就不要先考虑区间的范围。
先考虑合法性,也就是直接寻找符合条件的区间
考虑区间合法满足的条件。
首先,在一个区间中肯定是要满足最大值的位置max要在最小值的位置min后面的,即使max>min
可以发现,如果这个是存在的话,答案肯定是要尝试更新的。
如果不能更新的话,那么这个区间不代表就没有答案了。
所以我们还需要考虑一下在哪里会有答案。
对于一个max<min的区间
我们把他分为3个区间

其中的max和min的位置就是最大值和最小值的位置。
因为max在min的后面,所以这整个大区间就不可能会有答案。
所以我们就用max为右边界,min为左边界,再次分割出两个区间。
这就是区间1和3的由来。
区间2是剩下的。
awa
然后对于中间有解的情况
就是这样的

其中的区间2是已经有解的了,所以我们顶着min和max再次分割出两个区间。
就是区间1和3.
然后进行递归,就是答案了。
为了快速的统计最大值和最小值以及他们的位置,我们就用st表(这非常的显而易见)
然后就没了。
awa
code
#include<bits/stdc++.h> #define ll long long using namespace std; ll n,m,a[100001]; ll maxn[100001][27],b[100001][27]; ll minn[100001][27],c[100001][27]; ll ans,logn[100001]; inline ll read() { char c=getchar();ll a=0,b=1; for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1; for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48; return a*b; } void get_maxx(ll x,ll y)//为了记录最大值和最小值的位置而被魔改的转移 { if(maxn[x][y-1]<maxn[x+(1<<y-1)][y-1]) { maxn[x][y]=maxn[x+(1<<y-1)][y-1]; b[x][y]=b[x+(1<<y-1)][y-1]; } else { maxn[x][y]=maxn[x][y-1]; b[x][y]=b[x][y-1]; } } void get_minn(ll x,ll y) { if(minn[x][y-1]<minn[x+(1<<y-1)][y-1]) { minn[x][y]=minn[x][y-1]; c[x][y]=c[x][y-1]; } else { minn[x][y]=minn[x+(1<<y-1)][y-1]; c[x][y]=c[x+(1<<y-1)][y-1]; } } ll gax(ll l,ll r) { ll s=logn[(-l)+r+1]; if(maxn[l][s]<maxn[r-(1<<s)+1][s])return b[r-(1<<s)+1][s]; else return b[l][s]; } ll gin(ll l,ll r) { ll s=logn[(-l)+r+1]; if(minn[l][s]>minn[r-(1<<s)+1][s])return c[r-(1<<s)+1][s]; else return c[l][s]; } void Find(ll l,ll r) { ll x=gin(l,r),y=gax(l,r); if(x==y)return ; else { if(x<y) { ans=max(ans,(-x)+y+1); if(abs(x-l)>ans)Find(l,x-1); if(abs(r-y)>ans)Find(y+1,r); } else//x>y { if(abs(y-x)-1>ans)Find(y+1,x-1); if(abs(l-y)+1>ans)Find(l,y); if(abs(r-x)+1>ans)Find(x,r); } } } int main() { n=read(); logn[0]=-1; for(ll i=1;i<=n;i++) a[i]=minn[i][0]=maxn[i][0]=read(),c[i][0]=b[i][0]=i,logn[i]=logn[i>>1]+1; for(ll j=1;j<=19;j++) { for(ll i=1;i+(1<<j)-1<=n;i++) { get_maxx(i,j); get_minn(i,j); } } Find(1,n); cout<<ans<<endl; return 0; }



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】