2020 6 3 树状数组2 数羊

 

 

 这其实是一个很经典的问题的改版，但是在做法上也没有很大的改变。
原本的题目是，给点一个序列，求三元组（i,j,k）使得i<j<k&&a[i]<a[k]<a[j]的个数.
这种其实就是两个树状数组，分别维护一下i<j&&a[i]<a[j]和i>j&&a[i]>a[j]的数量就好了

但是这题求的是i<j<k&&a[i]<a[k]<a[j]
这样就很难搞了。
因为我们无法找到一个点能够同时在两个条件中和其他的两个点都相关
说通俗点，就是找不到一个点能够保证两个条件都成立，所以，就要换一个角度
这样的问题是很难解决的，考虑转化。
其实题目要求的就是这样的三元数对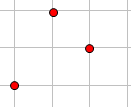

 

 

 (高低只表示相对的大小，不表示具体的数值)

我们可以很方便的求出像这样的数对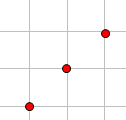

 

 这两个加起来，就是第一个点固定小于全部的数，第2,3个点的相对大小随机的全部方案数
所以只用把第一个点固定最小的情况算出来，这题就解决了。
这也是很好搞的，直接计算i前面小于a[i]的数的数量就好了。
然后直接算出后面的数量，在往答案上加上(cnt-1)*cnt/2 就好了(cnt指的是后面比a[i]小的数)
最后减去前面说的不合法情况就是真正的答案了。

 AC!

awa

code

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll lowbit(ll x){return x&(-x);}
ll n,a[1000001],tot;
ll f[1000001];//维护******的个数
ll fr[1000001];//维护i<j<k且a[i]>a[j]>a[k]的个数
ll fl[1000001];//维护左边比a[i]小的数的个数
ll fv[1000001];//维护左边比a[i]大的数的个数 
ll ans;
ll pos[1000001]; 
inline ll read()
{
    char c=getchar();ll a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
void add(ll x,ll k)
{
    while(x<=n)
    {
        f[x]+=k;
        x+=lowbit(x);
//        cout<<<<endl;
    }
}
ll ask(ll x)
{
    ll res=0;
    while(x>0)
    {
        res+=f[x];
        x-=lowbit(x);
    }
    return res;
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read();
    for(ll i=1;i<=n;i++)
    {
        a[i]=read();
        pos[a[i]]=i;
        add(a[i],1);
        fl[i]=ask(a[i]-1);
    }
    memset(f,0,sizeof(f));
    for(ll i=n;i>=1;i--)//i<j&&a[i]<a[j]的个数 
    {
        add(a[i],1);
        fr[i]=ask(n)-ask(a[i]);
        ans-=(fl[i]*fr[i]);
    }
    memset(f,0,sizeof(f));
    for(ll i=n;i>=1;i--)//i<j<k&&a[i]>a[j]>a[k]的个数 
    {
        ll cnt=ask(n)-ask(pos[i]);
        ans+=cnt*(cnt-1)/2;        
//        cout<<pos[i]<<' '<<i<<endl;
        add(pos[i],1);
    }
    cout<<ans<<endl;
    return 0;
}

 

the end