2020 5 27 树状数组

 

 

 

 

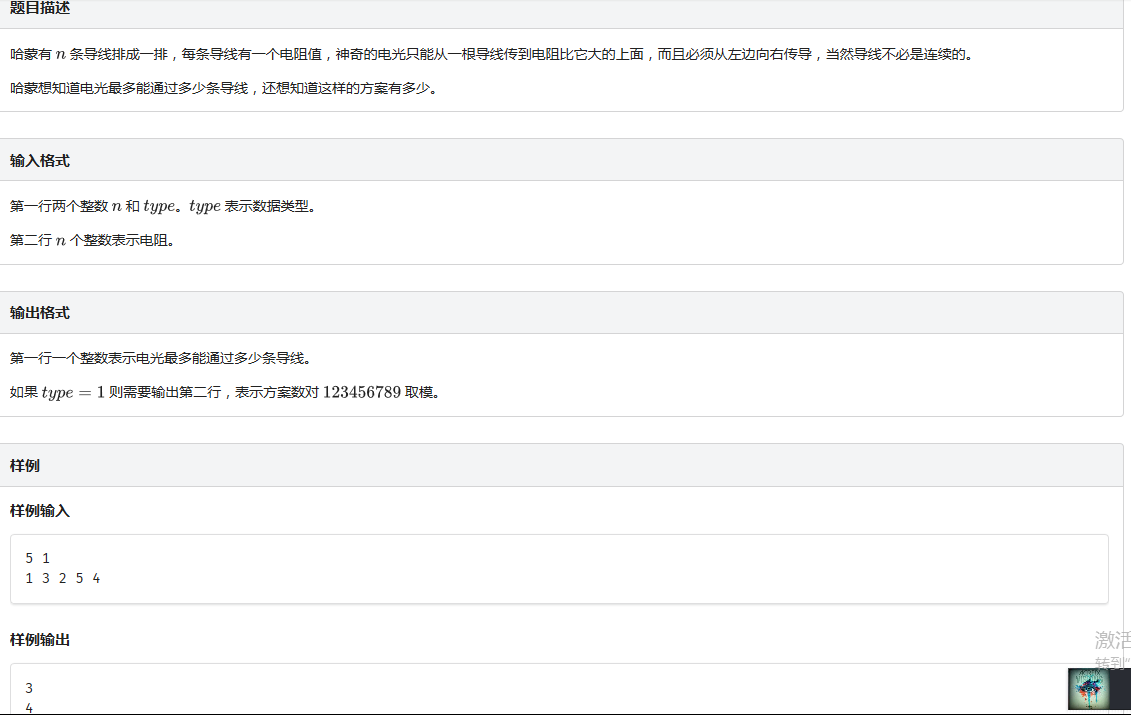
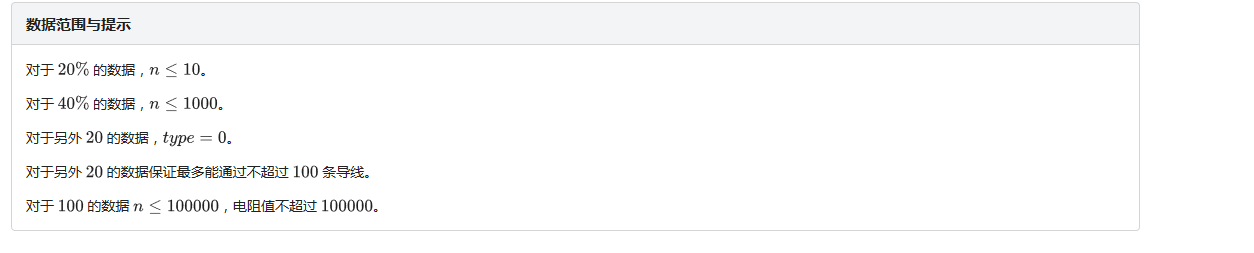
 这是一个比较显然的dp，最长不下降子序列。
但是他要求的时间是O(nlogn)，而且还要求的是求方案数。
原本的dp是O(n^2)的，会TLE
可以发现，其实这个是可以把方案数和dp值放在一起维护的。
我们就建一个树状数组，其中第x个数放的是当电阻小于x时的方案数和最长长度
每当读入一个数的时候，就先取出小于这个数的最长不下降子序列的数量
把取出的方案数++，因为加入了一个数，肯定是能够多至少一种方案的。
在用这个去尝试更新答案。
最后把这个数也加入树状数组，把它的全部能提供的方案数和价值也记录一下
如果在记录的时候，也就是树状数组使用它O（logn）的方法进行更改的时候，发现了长度的变化，那么就直接更新这个点答案就好了
其实这个进行更改的过程就是原来的dp的过程
但是因为是树状数组，更改仅仅是使用了O(logn)的时间就更改了全部的答案。
所以就很快了啦awa
但是为什么树状数组能维护的怎么好呢？仅仅是用了logn的时间就完成了O(n)的事情
主要是因为在原本的dp中，每一次的枚举上一个决策点都使用了大量的时间。这是没有必要的。
我们完全可以维护每一个决策点来使dp快速转移。
或者说是，其实每一个树状数组的汇合的点，就是储存了最优的决策的点，这个点中的决策时保证在目前情况下最优的。
那么，如果我更新的是这个点，就说明这个点的答案肯定是不行的了。到最后也是一样的。
至于方案数和这个是没关系的啦awa
方案数懒的搞了awa
各位dalao之间看代码吧awa
CODE

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=123456789;
inline ll read()
{
    char c=getchar();ll a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
int n,type,a[1000001];
struct tree
{
    int v,s;//长度，方案数
    inline void clear()
    {
        v=0;
        s=1;
        return;
    }
}t[1000001];
int lowbit(int x)
{
    return x&(-x);
}
inline int change(int x,tree y)
{
    while(x<=100000)
    {
        if(t[x].v<y.v)
        {
            t[x]=y;
        }
        else
        {
            if(y.v==t[x].v)
            {
                t[x].s+=y.s;
                t[x].s%=mod;
            }
        }
        x+=lowbit(x);
    }
}
inline tree ask(int x)
{
    tree res;
    res.clear();
    while(x>0)
    {
        if(t[x].v>res.v)
        {
            res=t[x];
        }
        else
        if(res.v==t[x].v)
        {
            res.s+=t[x].s;
            res.s%=mod;
        }
        x-=lowbit(x);
    }
    return res;
}
inline tree changeans(tree x,tree y)
{
    if(x.v<y.v)
    {
        return y;
    }
    else
    {
        if(x.v==y.v)
        {
            x.s+=y.s;
            x.s%=mod;
            return x;
        }
    }
    return x;
}
int main()
{
    tree ans;ans.clear();
    n=read();type=read();
    for(int i=1;i<=n;i++)
    {
        a[i]=read();
        tree x=ask(a[i]-1);
        x.v++;
        ans=changeans(ans,x);
        change(a[i],x);
    }
    cout<<ans.v%mod<<endl;
    if(type==1)cout<<ans.s%mod<<endl;
    return 0;
}